- Research
- Open access
- Published:
An effective method for network module extraction from microarray data
BMC Bioinformatics volume 13, Article number: S4 (2012)
Abstract
Background
The development of high-throughput Microarray technologies has provided various opportunities to systematically characterize diverse types of computational biological networks. Co-expression network have become popular in the analysis of microarray data, such as for detecting functional gene modules.
Results
This paper presents a method to build a co-expression network (CEN) and to detect network modules from the built network. We use an effective gene expression similarity measure called NMRS (Normalized mean residue similarity) to construct the CEN. We have tested our method on five publicly available benchmark microarray datasets. The network modules extracted by our algorithm have been biologically validated in terms of Q value and p value.
Conclusions
Our results show that the technique is capable of detecting biologically significant network modules from the co-expression network. Biologist can use this technique to find groups of genes with similar functionality based on their expression information.
Introduction
The development of high-throughput Microarray technologies has provided a range of opportunities to systematically characterize diverse types of biological networks. Biological networks can be broadly classified as protein interaction networks [1–3], metabolic networks [4–6] and gene co-expression networks [7]. These networks provide an effective way to summarize gene and protein correlations. In this paper, we focus on gene co-expression networks, which is an undirected graph where nodes represent gene and nodes are connected by an edge if the corresponding gene pairs are significantly co-expressed. Gene co-expression networks provide the association between individual genes in terms of their expression similarity and a network-level view of the similarity among a set of genes. In co-expression networks, two genes are connected by an undirected edge if their activities have significant association, as computed using gene expression measurements such as Pearson correlation, Spearman correlation, mutual information. Compared to gene regulatory networks, a gene co-expression network is built upon gene neighborhood relations, which give interesting geometric interpretations of the network. One of the most important applications of gene co-expression networks is to identify functional gene modules [8] or network modules, which are represented by the strongly connected regions of the co-expression network.
Problem formulation
Due to non-transitive nature of connections among genes, genes form a very complicated connectivity network with respect to a particular similarity measure in a gene expression data set. Such a connectivity network is often referred to as a co-expression network. A major use of this co-expression network is extraction of network modules that represent the strongly connected regions in the co-expression network. These modules may present highly co expressed genes, which are functionally similar.
In this paper, we propose an effective similarity measure for gene co-expression, develop an approach to prepare a co- expression network from a gene expression data set and mine the potential network modules from the built network. We aim to produce a graph, G={V,E} that presents the co-expression network with the following properties.
-
1.
Each vertex v∈V represents a gene.
-
2.
Each edge e∈E represents a connection between a pair of vertices v1,v2 where v1,v2 ∈V.
-
3.
There is an edge between two vertices v1,v2 ∈V if the similarity of the genes corresponding to the vertices is more than a user defined threshold.
Our contribution
We claim the following contributions in this paper.
-
We introduce an effective gene similarity measure NMRS.
-
We propose an approach to construct a co-expression network using NMRS.
-
We develop a spanning tree based method to extract the potential network modules.
Background
In the literature, a number of techniques have been proposed for gene co-expression network construction. When inferring co-expression networks from gene expression data, the algorithms take a gene expression dataset as primary input and then, by using a correlation-based proximity measure, constructs the corresponding co-expression networks. Frequently used correlation-based measures are Pearson correlation coefficient, Spearman correlation coefficient and Mutual information. Approaches such as [9, 10] used Pearson correlation coefficient to extract the association among genes in a co-expression network. The Spearman correlation coefficient is used as a gene expression similarity measure to construct co-expression network in [10]. [11], Steuer et al. [12] reports the use of Mutual Information to find similarly expressed gene pairs in such networks. While some studies attempted to apply algorithms directly to the adjacency matrices of networks to partition network nodes into groups [13, 14], other studies rely on special purpose algorithms for identifying subnetworks with certain properties [15].
Generally, in a co-expression network, the connections between genes are obtained from the absolute values of a co-expression measure. Several researchers have suggested to threshold this value of the co-expression measure to construct gene co-expression networks. There are two ways to pick a threshold: one way is picking a hard threshold (a number) based on the notion of statistical significance so that gene co-expression is encoded using binary information (connected=1, unconnected=0). The other way is called soft thresholding which weighs each connection by a number between 0 and 1. The drawbacks of hard thresholding include loss of information regarding the magnitude of gene connections and sensitivity to the choice of the threshold. Generally, hard thresholding results in unweighted networks while soft thresholding results in weighted networks.
Methodology
To construct the gene co-expression network, we use the general framework proposed by [16]. A new effective gene similarity measure called NMRS is used to construct the distance matrix. We use a hard thresholding based signum function to construct the adjacency matrix from the distance matrix. A spanning tree based approach is used to detect network modules in the co-expression network. Extracted network modules are projected as functional categories of genes and these modules are validated using p value and Q value. Our approach is explained next.
Define a gene expression measurement
To determine whether two genes have similar expression patterns, an appropriate similarity measure must be chosen [17]. To measure the level of concordance between gene expression profiles, we develop a gene co-expression measure called NMRS. The NMRS of gene d1=(a1, a2,…, a
n
) with respect to gene d2=(b1, b2,…, b
n
) is defined by 
where

NMRS as a metric
NMRS satisfies all the properties of a metric. We establish The non-negativity, symmetricity and triangular inequality properties for our measure in additional file 1.
Significance of NMRS
The most widely used proximity measures in gene expression data analysis are Euclidean distance, Pearson correlation coefficient, Spearman correlation coefficient, Mean squared residue etc. In co-expression network, the used proximity measure is expected to effectively detect the linear shifting patterns in the gene expression data. But none of the widely used proximity measures can satisfactorily serve this purpose. The Euclidean distance measures the distance between two data objects. But in this domain, the overall shapes of gene expression patterns (or profiles) are of greater interest than the individual magnitudes of each feature [18]. So Euclidean distance can not straight away detect shifting patterns, but bringing down all the genes to the same range of expression values can make this measure to detect shifting patterns. This normalization process involves an extra overhead. Along with shifting patterns Pearson correlation coefficient also detects scaling patterns and some other patterns which is normally not desired in a co-expression network and may lead to inclusion of genes which have considerable amount of difference between their expression levels. Spearman Rank Correlation Coefficient uses ranks to calculate correlation which can neither detect shifting patterns nor scaling patterns. Mean squared residue is good enough to detect shifting patterns, but the aggregate measure can not operate in a mutual mode, i.e. it can not find correlation between a pair of genes. A general comparison of these measures is presented in Table 1.
Let us consider a random gene pattern a as presented in Figure 1(a). Gene pattern b1 in Figure 1(b) has a shifting relationship with gene a. Gene pattern b8 in Figure 1(i) is a shifted as well as negatively correlated form of gene a. Figures 1(b)-1(h) present gene patterns b2, b3, b4, b5, b6 and b7 which are uniformly distributed intermediate patterns between genes b1 and b8. Figure 2 shows Pearson, Spearman and NMRS correlation of gene patterns b1-b8 with that of a. As usual the Spearman correlation was found to be concerned only about the rank information about the gene patterns. Interestingly, Pearson correlation was found to produce some undesired correlation values for the pairs a and b2, a and b3, a and b4, a and b4, a and b5, a and b6 and a and b7, which are neither shifting nor scaling patterns. The values of these patterns are given in Table 2. Our measure is found to effectively distinguish patterns across this uniform distribution from a shifted pattern (with a value 1) to a shifted and negatively correlated pattern (with value 0) of a given pattern as can be seen in Figure 2.
Compute an adjacency matrix
An adjacency matrix is obtained using a signum function based hard thresholding approach which encodes edge information for each pair of nodes in the co-expression network. Two genes d i and d j are connected if Dist(d i ,d j ) >δ, a user defined threshold. Based on the connected pairs, an adjacency matrix is computed as

Detect network modules
To detect subsets of nodes (modules) that are tightly connected to each other is an important aim of co-expression network analysis. In this paper, we use spanning trees and a topological overlap similarity measure [19] to find the network modules, since this measure is found to result in biologically meaningful modules. A tree T is a spanning tree of a connected graph G if T is a subgraph of G and it contains all vertices of G. We use Prim’s algorithm [20] to find a spanning tree of a undirected graph. However, unlike traditional Prim’s algorithm we find a spanning tree with maximum weight. For unweighed networks (i.e. a ij = 1 or = 0), the topological overlap matrix is defined by

where l ij = ∑ u a iu a ij , and k i = ∑ u a iu is the node connectivity.
Extract useful information
Extraction of useful biological information is one of the main usages of gene co-expression networks. From the constructed network, one can explore various important information such as functionality and pathways of genes, essential genes susceptible to diseases.
Proposed algorithm: Module Miner
Module Miner takes NMRS threshold, δ, as a input and works on a microarray gene data and constructs the gene co-expression network and finally network modules are extracted from the network. Our approach uses an effective similarity measure NMRS to form a co-expression network using signum function. The co-expression network is further explored to mine the potential network modules using a spanning tree based method and a connectivity measure called Topological Overlap Matrix.
The symbols provided in Table 3 and definitions given below are useful in discussing the proposed Module Miner algorithm.
Definition 1 A CEN can be defined by an undirected, graph G={V,E} where each v∈V corresponds to a gene and each edge e∈E corresponds a pair of genes d i , d j ∈D such that Dist(di, d j )≥δ.
Definition 2 Connected regions in a CEN are parts of the network where each pair of vertices is connected by a path. The ith connected region extracted from G can be defined as a graph  where
where  and
and  such that for any vertex
such that for any vertex  , there is at least one vertex
, there is at least one vertex  which are connected by an edge
which are connected by an edge  .
.
Definition 3 Maximum spanning tree of a weighted graph is a spanning tree obtained from ith connected region,
of a weighted graph is a spanning tree obtained from ith connected region,  can be defined as
can be defined as  , where the sum of TOM values associated with edges in
, where the sum of TOM values associated with edges in  is maximum compared to other spanning trees.
is maximum compared to other spanning trees.
Definition 4
Network modules
are highly connected regions of the co-expression network. The i
th
network module derived from j
th
connected region
 is defined as a set of vertices
is defined as a set of vertices
 if
if
-

and
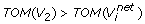 where
where
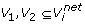 are obtained by removing the weakest edge of the maximum spanning tree built for the subgraph of G consisting of vertex set
are obtained by removing the weakest edge of the maximum spanning tree built for the subgraph of G consisting of vertex set
 or
or
-
TOM(V3)>TOM(V4) and
 where,
where,  are obtained by removing the weakest edge of the maximum spanning tree built for the subgraph of G consisting of vertex set V4.
are obtained by removing the weakest edge of the maximum spanning tree built for the subgraph of G consisting of vertex set V4.
Algorithm: Module Miner
The pseudo code of Module Miner is presented in Algorithm 1. In the pseudo code, lines 1-4 extracts the connected regions from the gene expression data. Lines 5-25 process each of the connected regions to extract the network modules. A maximum spanning tree is constructed using Prim’s algorithm [20] from a connected region with weights defined by topological overlap matrix in lines 6-8. Lines 9-10 find and remove the weakest edge from the spanning tree. Removal of this edge from the spanning tree leads to two subtrees which are processed in lines 11-23 to form either a connected module or a new connected region.

Algorithm complexity
The complexity of different steps of our method is presented in this section.
-
The preparation of the distance matrix involves a complexity of O(n×n-1)/2, where n is the number of genes.
-
Finding connected regions from the co-expression network requires a complexity of O(n).
-
Computation of the TOM matrix involves a complexity of O(n c ×(d c ×(d c -1)/2)), where n c is the total number of connected regions and d c is the average number of genes in the connected regions.
-
Finding a maximum spanning tree consumes a complexity of
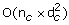 .
.
Experimental results
We implemented the Module Miner algorithm in MATLAB and tested it on five benchmark microarray datasets mentioned in Table 4. The test platform was a SUN workstation with Intel(R) Xenon(R) 3.33 GHz processor and 6 GB memory running Windows XP operating system.
Validation
The performance of Module Miner on the five publicly available benchmark microarray dataset is measured in terms of p value and Q value.
p value
Biological significance of the sets of genes included in the extracted network modules are evaluated based on p values [21]. p value signifies how well these genes match with different Gene Ontology(GO) categories. A cumulative hypergeometric distribution is used to compute the p value. A low p-value of the set of genes in a network module indicates that the genes belong to enriched functional categories and are biologically significant. From a given GO category, the probability p of getting k or more genes within a cluster of size n, is defined as

where f and g denote the total number of genes within a category and within the genome respectively.
To compute p-value, we used a tool called FuncAssociate [22]. FuncAssociate computes the hyper geometric functional enrichment score based on Molecular Function and Biological Process annotations. The enriched functional categories for some of the network modules obtained by Module miner on the datasets are presented in Tables 5 and 6. The co-expression network modules produced by Module Miner contains the highly enriched cellular components of DNA replication, DNA repair, DNA metabolic process, response to DNA damage stimulus, nuclear nucleosome, nucleosome, nucleosome assembly, protein-DNA complex, cell wall assembly, meiosis, cell differentiation, sporulation resulting in formation of a cellular spore, sporulation, anatomical structure formation involved in morphogenesis, cellular developmental process, reproductive cellular process, cell cycle phase, developmental process, cell cycle process etc with p-values of 7.69 × 10–27, 3.93 × 10–25, 1.03 × 10–26, 1.23 × 10–23, 2.32 × 10–28, 5 .12 × 10–27, 7.27 × 10–23, 2.06 × 10–20, 3.84 × 10–32, 1.41 × 10–31, 1.19 × 10–38, 9.65 × 10–36, 1.34 × 10–20, 2.52 × 19–34, 1.93 × 10–28 and 6.91 × 10–27 being the highly enriched one. From the given p values, we can conclude that Module Miner shows a good enrichment of functional categories and therefore project a good biological significance.
Q value
The Q-value [23] for a particular gene G is the proportion of false positives among all genes that are as or more extremely differentially expressed. Equivalently, the Q-value is the minimal False Discovery Rate(FDR) at which this gene appears significant. The GO categories and Q-values from a FDR corrected hypergeometric test for enrichment are reported in GeneMANIA. Q-values are estimated using the Benjamini Hochberg procedure. Different GO categories of the co-expression networks produced by Module miner are displayed up to a Q-value cutoff of 0.1 in Table 7, 8, 9, 10 and 11. The co-expression network modules produced by Module Miner contains the highly enriched cellular components of sporulation resulting in formation of a cellular spore, spore wall assembly, ascospore wall assembly, ascospore formation, sexual sporulation, spore wall biogenesis, ascospore wall biogenesis, sexual sporulation resulting in formation of a cellular spore, cell development cell wall assembly, reproductive process in single-celled organism, cell differentiation, fungal-type cell wall biogenesis, reproductive developmental process, reproductive process, reproductive cellular process, reproduction of a single-celled organism, cell wall biogenesis, sexual reproduction, anatomical structure development, anatomical structure morphogenesis , M phase, meiotic cell cycle, meiosis, M phase of meiotic cell cycle etc with Q-values of 1.53 × 10–34, 3.43 × 10–33, 2.59 × 10–32, 6.93 × 10–30, 1.40 × 10–29, 1.86 × 10–25, 9.90 × 10–25, 1.25 × 10–24, 4.83 × 10–24, 5.45 × 10–24, 2.10 × 10–23, 1.62 × 10–21, 2.74 × 10–21 being the highly enriched one. From the results of Q value, we arrive at the conclusion that the genes in a network module cluster obtained by Module Miner seem to be involved in similar functions.
We have used GeneMANIA [24] which is a flexible, user-friendly web interface for generating hypotheses about gene function, analyzing gene lists and prioritizing genes for functional assays. Given a query list, GeneMANIA extends the list with functionally similar genes that it identifies using available genomics and proteomics data. GeneMANIA displays results as an interactive network, illustrating the functional relatedness of the query and retrieved genes. GeneMANIA currently supports different networks including co-expression, physical interaction, genetic interaction, co-localization etc. On a given set of genes and their connectivity information, GeneMANIA also assigns coverage ratios as percentage to each of these networks with respect to the annotated genes in the genome. The percentage of co-expression on network modules produced by Module Miner is given in Table 12. The values are obtained by choosing the default network weighting option i.e. automatically selected weighing method. Visualization of some of the co-expression networks generated by GeneMANIA for the datasets are presented in Figures 3, 4, 5.
Conclusion and future work
In this paper, an effective gene expression similarity measure NMRS is introduced, which is used to construct the co-expression network through a signum function based hard thresholding scheme. Finally, network modules are extracted from the network using maximum spanning tree and topological overlap matrix. However, soft thresholding method can be used to construct the adjacency matrix to reduce information loss. Generalized Topological Overlap Measure [25] can be used instead of Topological Overlap Measure to get more accurate results. There is scope to design supervised models to derive gene regulatory network from the co-expression network.
References
Wagner A: How the global structure of protein interaction networks evolves. Proc Biol Sci 2003, 270: 457–466. 10.1098/rspb.2002.2269
Ito T, Chiba T, Ozawa R, Yoshida M, Hattori M, Sakaki Y: A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proceedings of the National Academy of Sciences of the United States of America 2001, 98: 4569–4574. 10.1073/pnas.061034498
Jeong H, B AL, Mason SP, Oltvai ZN: Lethality and centrality in protein networks. Nature 2001, 411: 41–42. 10.1038/35075138
Wagner A, Fell DA: The small world inside large metabolic networks. Proceedings. Biological sciences /The Royal Society 2001, 268(1478):1803–1810. 10.1098/rspb.2001.1711
Ma H, Zeng AP: Reconstruction of metabolic networks from genome data and analysis of their global structure for various organisms. Bioinformatics 2003, 19: 270–277. 10.1093/bioinformatics/19.2.270
Jeong H, B AL, Mason SP, Oltvai ZN: The large-scale organization of metabolic networks. Nature 2000, 407: 651–654. 10.1038/35036627
van Noort V, Snel B, Huynen M: The yeast coexpression network has a small-world, scale-free architecture and can be explained by a simple model. EMBO Reports 2004, 5(3):280–284. 10.1038/sj.embor.7400090
Ruan J, Dean A, Zhang W: A general co-expression network-based approach to gene expression analysis: comparison and applications. BMC Systems Biology 2010., 4:
Butte AJ, Tamayo P, Slonim D, Golub TR, Kohane IS: Discovering functional relationships between RNA expression and chemotherapeutic susceptibility using relevance networks. Proceedings of the National Academy of Sciences of the United States of America 2000, 97: 12182–12186. [http://dx.doi.org/10.1073/pnas.220392197] 10.1073/pnas.220392197
D’Haeseleer P, Liang S, Somogyi R: Genetic Network Inference: Prom Co-Expression Clustering To Reverse Engineering. 2000.
Butte AJ, Kohane IS, Kohane IS: Mutual Information Relevance Networks: Functional Genomic Clustering Using Pairwise Entropy Measurements. Pacific Symposium on Biocomputing 2000, 5: 415–426.
Steuer R, Kurths J, Daub CO, Weise J, Selbig J: The mutual information: Detecting and evaluating dependencies between variables. Bioinformatics 2002, 18: S231-S240. 10.1093/bioinformatics/18.suppl_2.S231
Lee HK, Hsu AK, Sajdak J, Qin J, Pavlidis P, Alerting E, Lee HK, Hsu AK, Sajdak J, Qin J, Pavlidis P: Coexpression analysis of human genes across many microarray data sets. Genome Res 2004, 14: 1085–1094. 10.1101/gr.1910904
Expression G, Zhu D, Hero AO, Cheng H, Khanna R: Network constrained clustering for gene microarray data. Bioinformatics 2005, 21: 4014–4021. 10.1093/bioinformatics/bti655
Stuart JM, Segal E, Koller D, Kim SK: A gene-coexpression network for global discovery of conserved genetic modules. Science 2003, 302: 249–255. 10.1126/science.1087447
Zhang B, Horvath S: A general framework for weighted gene co-expression network analysis. Statistical applications in genetics and molecular biology 2005., 4:
Yona G, Dirks W, Rahman S, Lin DM: Effective similarity measures for expression profiles. Bioinformatics 2006, 22(13):1616–1622. 10.1093/bioinformatics/btl127
Jiang D, Tang C, Zhang A: Cluster Analysis for Gene Expression Data: A Survey. IEEE Transactions on Knowledge and Data Engineering 2004, 16: 1370–1386. 10.1109/TKDE.2004.68
Ravasz E, Somera AL, Mongru DA, Oltvai ZN, Barabási AL: Hierarchical organization of modularity in metabolic networks. Science (New York, N.Y.) 2002, 297(5586):1551–1555. 10.1126/science.1073374
Prim RC: Shortest connection networks and some generalizations. Bell System Technology Journal 1957, 36: 1389–1401.
Tavazoie S, Hughes JD, Campbell MJ, Cho RJ, Church GM: Systematic determination of genetic network architecture. Nature Genetics 1999.
Berriz GF, King OD, Bryant B, Sander C, Roth FP: Characterizing gene sets with FuncAssociate. Bioinformatics (Oxford, England) 2003, 19: 2502–2504. 10.1093/bioinformatics/btg363
Benjamini Y, Hochberg Y: Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal of the Royal Statistical Society. Series B (Methodological) 1995, 57: 289–300.
Warde-Farley D, Donaldson SL, Comes O, Zuberi K, Badrawi R, Chao P, Franz M, Grouios C, Kazi F, Lopes CT, Maitland A, Mostafavi S, Montojo J, Shao Q, Wright G, Bader GD, Morris Q: The GeneMANIA prediction server: biological network integration for gene prioritization and predicting gene function. Nucleic Acids Research 2010, 38: W214-W220. 10.1093/nar/gkq537
Yip AM, Horvath S: Gene network interconnectedness and the generalized topological overlap measure. BMC Bioinformatics 2007., 8:
Acknowledgment
This paper is an outcome of a research project supported by (1) DST, Govt. of India in collaboration with ISI, Kolkata and (2) National Science Foundation, USA under grants CNS-095876 and CNS-085173.
This article has been published as part of BMC Bioinformatics Volume 13 Supplement 13, 2012: Selected articles from The 8th Annual Biotechnology and Bioinformatics Symposium (BIOT-2011). The full contents of the supplement are available online at http://www.biomedcentral.com/1471-2105/13/S13/S1
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author(s) declare that they have no competing interests.
Electronic supplementary material
12859_2012_5289_MOESM1_ESM.pdf
Additional file 1: NMRS as a metric This additional file 1 presents the proofs of different metric properties of NMRS measure. (PDF 136 KB)
Rights and permissions
Open Access This article is published under license to BioMed Central Ltd. This is an Open Access article is distributed under the terms of the Creative Commons Attribution License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mahanta, P., Ahmed, H.A., Bhattacharyya, D.K. et al. An effective method for network module extraction from microarray data. BMC Bioinformatics 13 (Suppl 13), S4 (2012). https://doi.org/10.1186/1471-2105-13-S13-S4
Published:
DOI: https://doi.org/10.1186/1471-2105-13-S13-S4



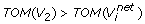 where
where
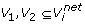 are obtained by removing the weakest edge of the maximum spanning tree built for the subgraph of G consisting of vertex set
are obtained by removing the weakest edge of the maximum spanning tree built for the subgraph of G consisting of vertex set
 where,
where,  are obtained by removing the weakest edge of the maximum spanning tree built for the subgraph of G consisting of vertex set V4.
are obtained by removing the weakest edge of the maximum spanning tree built for the subgraph of G consisting of vertex set V4.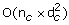 .
.

