- Research article
- Open access
- Published:
Integrating functional genomics data using maximum likelihood based simultaneous component analysis
BMC Bioinformatics volume 10, Article number: 340 (2009)
Abstract
Background
In contemporary biology, complex biological processes are increasingly studied by collecting and analyzing measurements of the same entities that are collected with different analytical platforms. Such data comprise a number of data blocks that are coupled via a common mode. The goal of collecting this type of data is to discover biological mechanisms that underlie the behavior of the variables in the different data blocks. The simultaneous component analysis (SCA) family of data analysis methods is suited for this task. However, a SCA may be hampered by the data blocks being subjected to different amounts of measurement error, or noise. To unveil the true mechanisms underlying the data, it could be fruitful to take noise heterogeneity into consideration in the data analysis. Maximum likelihood based SCA (MxLSCA-P) was developed for this purpose. In a previous simulation study it outperformed normal SCA-P. This previous study, however, did not mimic in many respects typical functional genomics data sets, such as, data blocks coupled via the experimental mode, more variables than experimental units, and medium to high correlations between variables. Here, we present a new simulation study in which the usefulness of MxLSCA-P compared to ordinary SCA-P is evaluated within a typical functional genomics setting. Subsequently, the performance of the two methods is evaluated by analysis of a real life Escherichia coli metabolomics data set.
Results
In the simulation study, MxLSCA-P outperforms SCA-P in terms of recovery of the true underlying scores of the common mode and of the true values underlying the data entries. MxLSCA-P further performed especially better when the simulated data blocks were subject to different noise levels. In the analysis of an E. coli metabolomics data set, MxLSCA-P provided a slightly better and more consistent interpretation.
Conclusion
MxLSCA-P is a promising addition to the SCA family. The analysis of coupled functional genomics data blocks could benefit from its ability to take different noise levels per data block into consideration and improve the recovery of the true patterns underlying the data. Moreover, the maximum likelihood based approach underlying MxLSCA-P could be extended to custom-made solutions to specific problems encountered.
Background
In contemporary biology, it becomes more widespread to study complex biological processes by collecting and analyzing measurements on the same entities from different sources, such as transcriptomics, metabolomics, ChIP-chip, or proteomics. The data originating from such measurements can often be organized in matrices pertaining to experimental units (e.g., tissues or culture samples) and variables (e.g., genes or metabolites) that were measured on these experimental units. The experimental units, also referred to as objects, constitute the experimental mode of the data, and the measured biochemical compounds the variable mode. We will denote such matrices consisting of measurements originating from different sources by data blocks.
Data blocks with information on the same entities stemming from different sources share one of the data modes; as such we will further denote them by the term 'coupled data'. For instance, Ishii and coworkers [1] simultaneously collected metabolomics, transcriptomics, and proteomics measurements from Escherichia coli chemostat cultures with different mutants and environmental conditions. This yields measurements coupled via the experimental mode. Other examples of publications involving this type of data are [2, 3]. As an alternative, data blocks can be coupled via the variable mode. This occurs, for instance, in experiments in which transcriptomics measurements are coupled with ChIP-chip measurements [4], or even with ChIP-chip and motif data [5].
Often, the purpose of collecting coupled data will be to discover biological mechanisms that underlie the behavior of the variables in the different data blocks. For example, when the measurements originate from experiments in which metabolomics and transcriptomics analyses were conducted, the researcher could be interested in identifying regulatory mechanisms that coordinate a joint response on metabolome and transcriptome level.
To arrive at a comprehensive synthesis of the information on biological mechanisms underlying coupled data blocks, the data blocks have to be analyzed simultaneously. For such a synthesis, the family of simultaneous component analysis (SCA) methods is a natural choice. SCA methods search for important patterns in the data blocks and reveal the contributions of the variables and the experimental units to these patterns, similar to principal component analysis (PCA). The identified patterns can subsequently aid the discovery of the regulatory mechanisms underlying the data.
However, a simultaneous analysis of multiple data blocks may be hampered by the data blocks being heterogeneous in a number of respects. For instance, measurements originating from different functional genomics platforms can be subject to different amounts measurement error, or noise related to the accuracy of the platforms in question.
The noise present in the different data blocks can obscure the data patterns. Therefore, it can become more difficult to extract information regarding these patterns. For this reason, it could be fruitful to take data block noise into consideration in the data analysis. In particular, when data blocks are subject to different amounts of noise, it seems desirable to treat the data block with more noise with more caution.
Yet, the different noise levels should be known to be able to take these into consideration. Often however, it is unknown how much noise is present in each data block. If this were the case, a method is needed that also estimates the noise in each data block. Such a method was proposed recently in the psychometrics field: MxLSCA-P, a maximum likelihood based SCA method (Wilderjans, T.F., Ceulemans, E., Van Mechelen, I., van den Berg, R.A.: Simultaneous analysis of coupled data matrices subject to different amounts of noise, submitted). MxLSCA-P explicitly estimates the noise levels per data block and integrates these estimations in the overall analysis. In a simulation study, MxLSCA-P outperformed standard SCA-P [6] when recovering the underlying structure of simulated data blocks that were subject to different noise levels.
One may wish to translate the results of the simulation study mentioned above to the analysis of coupled functional genomics data. There are, however, two obstacles that prevent a direct translation. First, the data blocks simulated in the previous study were coupled via the variable mode, while functional genomics measurements often pertain to measurements coupled via the experimental mode [1–3]. Different coupling leads to a rather different kind of analysis, in particular with regard to the type of preprocessing that is linked to different SCA methods [7–10]. It is therefore not self-evident that the previous results hold for data blocks coupled via the experimental mode. Second, the simulation study did not consider data aspects that are typical for functional genomics, such as, having more variables than objects, and moderate to high correlations between variables (e.g., between two co-regulated genes) as the simulation was based on randomly generated components.
In this paper we will present a new simulation study to overcome these obstacles and to ascertain the relevance of MxLSCA-P for the analysis of functional genomics data coupled via the experimental mode. For this purpose we will determine the performance of MxLSCA-P in a context in which (i) the experimental mode is shared; and (ii) the correlations between variables are realistic in that they mimic the correlations observed in a real life microbial metabolomics data set consisting of two coupled GC/MS (gas chromatography combined with mass spectrometry) and LC/MS (liquid chromatography combined with mass spectrometry) data blocks. In addition, we will also apply standard SCA-P and MxLSCA-P to the real life metabolomics data set itself. Before presenting the results of the analysis of simulated and real-life data sets, we will now first explain SCA-P and MxLSCA-P. Subsequently, we will outline the problem and setup of our new simulation study.
Simultaneous component analysis
Notation
In this paper matrices and vectors will be indicated by bold uppercase and lowercase characters as in Kiers [11]. Elements will further be denoted by lowercase running indices that range from 1 to the corresponding uppercase characters. For instance, the number of objects in a data block will be indexed by i, running from 1 to I.
General SCA decomposition
The family of SCA methods [10] comprises a wide range of component methods that share two characteristics. First, they reduce the dimensionality of the data blocks by decomposing the data blocks in components, and second they do so while minimizing the loss of information. The SCA methods distinguish themselves from other components methods [10] by (i) simultaneously decomposing coupled data blocks with the different data blocks taking exchangeable roles, and (ii) allowing for block-specific weighting of data blocks to capture particular aspects of the data blocks more adequately.
In general, given a set of K data blocks X k that share an object mode with I objects and J k variables, and a set of prespecified block-specific weights w k , a SCA decomposition reads as follows:

with T(I × R) denoting a score matrix for R components shared by all K data blocks, P k (J k × R) the accompanying block-specific loadings, and E k (I × J k ) a residual matrix.
This decomposition of data blocks that share the object mode will be the reference decomposition in this paper. For other situations in which the data blocks share a variable mode, the SCA decomposition is given by:

with T k (I k × R) denoting a block-specific score matrix for R components, P(J × R) the loadings shared by all data blocks, and E k (I k × J) a residual matrix.
Model estimation
For the estimation of T and P k the following objective function is minimized:

The optimal matrices T and P k that minimize (3) can be estimated on the basis of the following identity:

Where X
c
= [w1X1...w
k
X
k
...w
K
X
K
] with size  is the concatenation of all w
k
X
k
, and
is the concatenation of all w
k
X
k
, and  with size
with size  is the concatenation of all P
k
; the estimates then can be obtained by means of a singular value decomposition (SVD) [10]. For identification purposes, the components can be constrained to have a principal axis orientation and T or P
c
to be orthonormal.
is the concatenation of all P
k
; the estimates then can be obtained by means of a singular value decomposition (SVD) [10]. For identification purposes, the components can be constrained to have a principal axis orientation and T or P
c
to be orthonormal.
The SVD of X c reads as follows:

If T is chosen to be columnwise orthonormal, T can be obtained by choosing the R left singular vectors associated with the R largest singular values in S. The loadings P c are then obtained by multiplication of the R right singular vectors with the R associated largest singular values:

where the subscript 'R' indicates the R largest singular values and accompanying singular vectors. In case P c is chosen to be orthonormal, P c is put equal to V R and T to U R S R .
SCA with equal block weights
SCA with equal block weights (w1 = ... = w K = w > 0) was proposed in the psychometrics literature as SCA-P [6] and in the chemometrics literature as SUM-PCA [12]. Both methods fit the general SCA decomposition as methods in which equal weights are applied to the different data blocks. In the remainder of this paper we will refer to this method as SCA-P.
Choosing equal block weights implies that all the data entries in the different data blocks are considered equally important and that no further block-specific adjustments are made to increase or decrease their relative influence. This approach was coined a 'one entry, one vote' approach [13]. The objective function of this method is:

MxLSCA-P
MxLSCA-P (Wilderjans, et al.: submitted) is a stochastic extension of the generic SCA method (1). Unlike SCA-P, it assumes that the residuals in E k follow a normal distribution with a mean of zero and an unknown block-specific variance:

The minus loglikelihood function for the MxLSCA-P method is (Wilderjans, et al.: submitted):

in which c denotes a constant term that does not influence the minimization of the minus loglikelihood function. (This equation generalizes the equivalent equation in (Wilderjans, et al.: submitted) that pertained to the two block case. We minimize the minus loglikelihood in line with the optimizations discussed previously.) The improved performance of MxLSCA-P in the previous simulation study (Wilderjans, et al.: submitted) can be understood from the different model assumptions made. SCA-P implicitly assumes that noise across the different data blocks is identically distributed, i.e., it maximizes the likelihood function based on the assumption that the noise is distributed identically in the different data blocks. When this assumption is violated and the noise is distributed differently, the SCA-P model becomes misspecified, unlike MxLSCA-P that specifically allows for those differences.
The objective function of MxLSCA-P (9) differs from the general objective function for SCA methods (3) by the introduction of block-specific noise parameters σ k . These noise parameters act as a weight to the data blocks and in a new term 'IJ k log σ k '. Unlike in the general SCA decomposition, in MxLSCA-P the block weights are to be estimated as an integrated part of the analysis.
The parameters of MxLSCA-P (σ k , T, and P k ) cannot be estimated directly via an SVD. Therefore an alternating least squares (ALS) algorithm [14, 15] was developed (Wilderjans, et al.: submitted).
In an ALS algorithm, the parameters to be estimated are split into subsets that are alternatingly re-estimated conditionally on each other. In particular, the following procedure is followed:
-
1.
The algorithm is initiated by choosing values for σ k . These starting values for σ k can be determined randomly or rationally (e.g., based on a SCA-P). It is advised to use multiple different starting values to avoid getting stuck in local minima.
-
2.
The scores T and loadings P k are estimated conditional on the values of σ k via an SVD. This SVD optimizes the following part of the objective function:
 .
. -
3.
New estimations
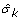 of σ
k
are calculated conditional on the previous estimations of
of σ
k
are calculated conditional on the previous estimations of  and
and 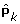 :
:  (10)
(10) -
4.
The current value of the objective function (9) is calculated.
The second, third, and fourth step are repeated until a convergence criterion is met (e.g., changes in the objective function below a prespecified threshold).
Problem and setup of the simulation study
A simulation study was set up to assess the performance of the SCA-P and MxLSCA-P methods for the analysis of functional genomics data blocks coupled via the experimental mode. The performance of the methods was evaluated in terms of their ability to recover the true structures (Tm,  ,
,  ,
, 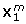 , and
, and 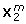 ) underlying two simulated data blocks subject to different simulation settings. To improve the realism of the simulations, the data blocks were simulated using the correlation structure of the variables as observed in a real life GC/MS and LC/MS microbial metabolomics data set (see Methods section).
) underlying two simulated data blocks subject to different simulation settings. To improve the realism of the simulations, the data blocks were simulated using the correlation structure of the variables as observed in a real life GC/MS and LC/MS microbial metabolomics data set (see Methods section).
Furthermore, different data characteristics that could influence the analysis of coupled functional genomics data blocks were varied. In particular, the following characteristics were included as design factors (see Methods section for detailed information):
-
Noise level of the data blocks. Noise can hamper the recovery of the true data structures, especially if the noise levels of different coupled functional genomics data blocks would differ. In the simulation study noise was manipulated via two factors: (i) the noise ratio between the two data blocks (factor Noise Ratio), and (ii) the total amount of noise on the data blocks (factor Noise Total).
-
Different numbers of variables per data block. In functional genomics research, different data blocks can considerably differ in the number of variables (e.g., metabolomics and transcriptomics data sets can consist of hundreds and thousands of variables, respectively). Moreover, the number of variables is generally larger than the number of objects which induces collinearity in the data [16, 17]. A SCA can be influenced by these factors in two ways. First, when the difference between the number of variables in different data blocks is large, the larger data block could dominate the analysis. Second, induced collinearity may hamper a correct estimation of the loadings.
In this simulation study a small and a large data block were simulated with different numbers of variables per data block (factor Number of variables). The total number of variables was always larger than the number of objects such that collinearity was always present. The large data block used the correlation structure observed in the GC/MS data set and the small data block the correlation structure of the LC/MS data set.
-
Relative importance of the data blocks. The variation present in one data block, and thus its importance, can differ from other data blocks. This could influence the recovery of the data structures, as data blocks with high variation can dominate other data blocks. The variation present in the data blocks is in an SVD expressed by the singular values. Here, the relative importance of a data block was manipulated by these singular values (factor Singular value).
In addition to these factors, a factor Methods was included in the experimental design, with SCA and MxLSCA-P as its two different levels. Recovery performance and the impact on it of the factors manipulated in the simulation study were analyzed by means of an analysis of variance (ANOVA).
Results
Performance of the SCA methods on simulated data
The recovery by the two SCA methods of the true data structures as measured by a Fisher-Z transformed modified RV coefficient [18] (RV-Z) was generally good. Recovery performance appeared to depend both on the specific structural aspect looked at, and on data characteristics as manipulated in the simulation study (Table 1). Below we will discuss the different data characteristics and their influence on the recovery of the true structural aspects.
Most importantly for the purpose of this research, the main effect of factor 'Method' and its interaction with 'Noise Ratio' appeared to be sizeable on the level of the recovery of the true scores (Tm) as well as of the true data block entries (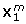 , and
, and 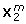 ). In particular, MxLSCA-P performed on average significantly better than SCA-P (Table 2). Moreover, as appears from Figure 1, in the case of the recovery of Tm,
). In particular, MxLSCA-P performed on average significantly better than SCA-P (Table 2). Moreover, as appears from Figure 1, in the case of the recovery of Tm, 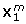 and
and 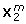 , MxLSCA-P especially outperforms SCA-P when the noise levels for the data blocks differ. For the recovery of Tm(Figure 1, left panel), recovery was best when the largest data block,
, MxLSCA-P especially outperforms SCA-P when the noise levels for the data blocks differ. For the recovery of Tm(Figure 1, left panel), recovery was best when the largest data block, 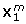 , was the least noisy. The recovery of a particular data block was further best (in absolute as well as relative sense) when that data block was subject to the least amount of noise (Figure 1, center panel:
, was the least noisy. The recovery of a particular data block was further best (in absolute as well as relative sense) when that data block was subject to the least amount of noise (Figure 1, center panel: 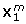 , right panel:
, right panel: 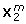 ). Furthermore, the interaction between 'Method' and 'Noise Total' was also sizable or the recovery Tm. This interaction showed that the benefit of MxLSCA-P is largest when the total noise level is low and the benefit becomes smaller for higher total noise levels. The advantage of MxLSCA-P over SCA-P for recovering the true underlying structures in the presence of different noise levels did not carry over to the recovery of the block-specific loadings
). Furthermore, the interaction between 'Method' and 'Noise Total' was also sizable or the recovery Tm. This interaction showed that the benefit of MxLSCA-P is largest when the total noise level is low and the benefit becomes smaller for higher total noise levels. The advantage of MxLSCA-P over SCA-P for recovering the true underlying structures in the presence of different noise levels did not carry over to the recovery of the block-specific loadings 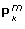 (Table 2). One might conjecture that this result is due to differences in the number of implicit constraints on the different constituents of the MxLSCA-P decomposition. The scores of the SCA decomposition are constrained to be identical for all data blocks; as a result, these scores may be prevented to be misguided by the data. The loadings, however, are not subject to such restriction, and, as a result have more freedom to deviate from the true model structure.
(Table 2). One might conjecture that this result is due to differences in the number of implicit constraints on the different constituents of the MxLSCA-P decomposition. The scores of the SCA decomposition are constrained to be identical for all data blocks; as a result, these scores may be prevented to be misguided by the data. The loadings, however, are not subject to such restriction, and, as a result have more freedom to deviate from the true model structure.
Mean recovery of Tm, , and for all combinations of the levels of 'Method' and 'Noise Ratio'. The recoveries of the different true structures Tm, 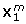 and
and 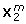 are given from left to right, respectively. The RV-Z is indicated on the y-axis. The two levels of 'Method' are indicated on the x-axis. The different lines indicate the different levels of the factor Noise Ratio (red, dashed, square = NoiseX1 < NoiseX2; solid blue, diamond = Equal; black, dashed, triangle = NoiseX1 > NoiseX2).
are given from left to right, respectively. The RV-Z is indicated on the y-axis. The two levels of 'Method' are indicated on the x-axis. The different lines indicate the different levels of the factor Noise Ratio (red, dashed, square = NoiseX1 < NoiseX2; solid blue, diamond = Equal; black, dashed, triangle = NoiseX1 > NoiseX2).
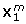 ,
, 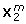 ,
,  , and
, and  .
.A sizeable main effect of 'Noise Total' was found for the recovery of all true structural aspects. This effect is obvious with more noise leading to a poorer recovery. Furthermore, for the recovery of all block-specific structural aspects (i.e., the true loadings  ,
,  , and the true data block entries of
, and the true data block entries of 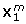 and
and 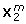 ), the main effect of 'Noise Ratio' was important as well, with the true structures being recovered better when the corresponding data block was less noisy. Furthermore, the interaction between 'Noise Total' and 'Noise Ratio' was substantial for the recovery of all data structures. This interaction was plotted in Figure 2 for the cases of the recovery
), the main effect of 'Noise Ratio' was important as well, with the true structures being recovered better when the corresponding data block was less noisy. Furthermore, the interaction between 'Noise Total' and 'Noise Ratio' was substantial for the recovery of all data structures. This interaction was plotted in Figure 2 for the cases of the recovery 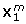 and
and 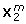 (for the block-specific loadings the pattern was similar). From Figure 2 it becomes clear that the effect of 'Noise Ratio' (i.e., better recovery when a particular block is relatively less noisy than the other as compared to a situation with a reverse noise ratio) shows up only in case of low to medium noise levels. In addition, a very good recovery is observed in case of the combination of a low total noise level and a Noise Ratio of 1; the latter is due to the fact that this particular combination implies a very low total noise level for the whole of the two data blocks (10-3%). For the recovery of the common scores, the interaction between 'Noise Total' and 'Noise Ratio' took a slightly different shape: Now the two conditions of 'Noise Ratio' that implied different noise levels for the two data blocks resulted in a better recovery in case of low and medium 'Total noise' levels.
(for the block-specific loadings the pattern was similar). From Figure 2 it becomes clear that the effect of 'Noise Ratio' (i.e., better recovery when a particular block is relatively less noisy than the other as compared to a situation with a reverse noise ratio) shows up only in case of low to medium noise levels. In addition, a very good recovery is observed in case of the combination of a low total noise level and a Noise Ratio of 1; the latter is due to the fact that this particular combination implies a very low total noise level for the whole of the two data blocks (10-3%). For the recovery of the common scores, the interaction between 'Noise Total' and 'Noise Ratio' took a slightly different shape: Now the two conditions of 'Noise Ratio' that implied different noise levels for the two data blocks resulted in a better recovery in case of low and medium 'Total noise' levels.
Mean recovery of 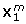 (left panel) and
(left panel) and 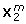 (right panel) for all combinations of the levels of 'Noise Total' and 'Noise Ratio'. The RV-Z is indicated on the y-axis. The three levels of 'Noise Total' are indicated on the x-axis. The different lines indicate the levels of the factor Noise Ratio (red, dashed, square = NoiseX1 < NoiseX2; solid blue, diamond = Equal; black, dashed, triangle = NoiseX1 > NoiseX2). The RV-Z values were averaged over the other factors, e.g., the factor Method.
(right panel) for all combinations of the levels of 'Noise Total' and 'Noise Ratio'. The RV-Z is indicated on the y-axis. The three levels of 'Noise Total' are indicated on the x-axis. The different lines indicate the levels of the factor Noise Ratio (red, dashed, square = NoiseX1 < NoiseX2; solid blue, diamond = Equal; black, dashed, triangle = NoiseX1 > NoiseX2). The RV-Z values were averaged over the other factors, e.g., the factor Method.
Analysis of real life microbial metabolomics data
To obtain an as complete as possible overview of the changes of the concentrations of metabolites in microbial metabolomics, multiple analytical platforms are required [19]. In this paper, E. coli metabolomics data consisting of metabolite concentrations that were obtained using GC/MS and LC/MS [20] were used. The data set consisted of 28 samples of batch fermentations with varying experimental conditions (e.g., low oxygen, succinate or D-glucose as sole carbon source, wild type or phenylalanine overproducing strain) taken at different time points. In general, different analytical platforms can perform differently with regard to reproducibility. Therefore, the analysis could potentially benefit from an MxLSCA-P approach that takes noise heterogeneity into account.
We subjected the data under study to MxLSCA-P and SCA-P analyses with three components. The three components were selected based on the scree plots of component analyses of the individual data blocks. Subsequently, the MxLSCA-P and SCA-P score plots were compared. The first two components appeared to be very similar: On the first component the samples obtained from succinate grown cells differed strongly from the other samples; the second component showed a separation between samples obtained under low oxygen conditions and samples obtained at late time points of both succinate grown cells and wild type cells. However, differences between the two methods became apparent for the third component. In particular, the scores on the third MxLSCA-P component for those conditions for which multiple time points were sampled as a function of time were plotted. For all these plots, profiles resembling typical batch fermentation growth curves were found. In such a growth curve, the cells first grow fast as a sufficient amount of nutrients is available; next, when nutrients become depleted, growth is halted and the curve starts to decline. A typical example of such a profile in the MxLSCA-P scores is plotted in the upper left corner of Figure 3. For SCA-P, such typical profiles were also found for five experimental conditions (see e.g., Figure 3, upper right plot), but for two experimental conditions the patterns differed (see e.g., Figure 3, lower right plot). (Note that the profile in the lower right plot cannot simply be reflected to match the typical batch fermentation profile, as reflections of SCA scores and loadings can only be performed on the entire score or loading vector and not on a subset of it.)
Scores on the third component of MxLSCA-P and SCA-P. Scores on the third component of MxLSCA-P (left) and SCA-P (right) for experimental conditions 4 and 10 (from top to bottom the first and second row of panels, respectively). On the x-axis, the different time points of sampling are presented ranging from 'early' (1) to 'late' (3, 4, and 5). The y-axis indicates the score value in arbitrary units.
The pattern of the block-specific loadings further nicely complemented the pattern of the scores. In particular, inspection of the loadings on the third component for the LC/MS data block revealed high contributions for cell wall precursors for peptidoglycan biosynthesis [21, 22] (like UDP-N-AAGDAA and UDP-N-AAGD) and nucleotides (such as, UDP, UTP, CMP, CDP, and CTP) that are involved in a wide range of cellular processes, among which cell wall biosynthesis [22]. Cell wall biosynthesis can be linked to the growth phases in a batch fermentation, as metabolites involved in it are likely to fluctuate depending on these growth phases. For instance, during exponential growth, cell wall intermediates are required for growth and cell division, whereas during the stationary growth phase the demand for these intermediates is expected to drop.
The MxLSCA-P block-specific loadings for the third component pertaining to the GC/MS data block revealed consistently large contributions for uncharacterized disaccharides; for the corresponding SCA-P loadings this was less clearly the case. Within the context of this study, there are two likely roles for disaccharides in E. coli, which both could relate to variation in metabolite concentrations during the different phases of a batch fermentation: (i) In cell wall biosynthesis, the different parts of the cell wall have polysaccharides as a major constituent, for instance, in peptidoglycan [21, 22] and in lipopolysaccharides [22, 23]. (ii) Disaccharides could play a role in the internal storage of excess carbon source, during conditions under which another nutrient excluding carbon source is limiting.
Summarizing, in this case study MxLSCA-P seemed better able to extract biologically relevant information. MxLSCA-P provided a more consistent link to the growth phases of the batch fermentations, both through the common scores and through the LC/MC data block loadings. Also, the disaccharides involved in the MxLSCA-P loadings for the GC/MS block are likely to link up with cellular processes related to the different batch fermentation growth phases.
Discussion
MxLSCA-P was proposed to model coupled data blocks with heterogeneous noise levels. In a previous simulation study, MxLSCA-P was shown to outperform SCA-P in recovering the true structure underlying the data that did not consider typical problems encountered in functional genomics studies. In the study presented in this manuscript the previous study was extended to address these problems typical for functional genomics: (i) the data were coupled via the experimental mode, (ii) the simulations were based on correlation structures observed in real life data sets, (iii) collinearity was induced by ensuring the data had more variables than objects. Our results showed that MxLSCA-P also outperforms SCA-P in simulated data that mimic functional genomics data more closely. In particular, MxLSCA-P was better able to recover the true scores (Tm) and true data blocks (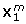 and
and 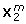 ) especially when the relative noise levels differed across data blocks. Furthermore, MxLSCA-P provided a more consistent and biologically more meaningful interpretation of the analysis of the E. coli metabolomics case study. Therefore MxLSCA-P seems to be the preferred choice over SCA-P for the kind of data we have studied, but probably for other kinds of data as well.
) especially when the relative noise levels differed across data blocks. Furthermore, MxLSCA-P provided a more consistent and biologically more meaningful interpretation of the analysis of the E. coli metabolomics case study. Therefore MxLSCA-P seems to be the preferred choice over SCA-P for the kind of data we have studied, but probably for other kinds of data as well.
In SCA-P, the data blocks are given equal a priori block weights as there is no a priori reason to treat the data blocks differently. MxLSCA-P is an extension of SCA-P in which, as an integrated part of the analysis, the equal a priori block weights are combined with data-driven a posteriori weights that reflect the noise levels of the different data blocks such as to de-emphasize the most noisy data blocks. Within the family of SCA methods, other methods exist that a priori weigh the data blocks differently to ensure that each block makes a "fair" contribution to the analysis. Such a weighting can be based on different conceptions of fairness [10], for instance, to ensure that each data block has the same amount of variation [12], or that data blocks with more redundant information are downweighted [24]. (The latter conception is the basis of multiple factor analysis, which was recently applied for the analysis of coupled functional genomics data blocks by de Tayrac and coworkers [25]). Those a priori weights to ensure a fair block weighting, however, do not take into account differences in measurement error, or noise levels. Indeed, analogous to SCA-P, in other SCA methods it is implicitly assumed that the data blocks have equally and independently normal distributed noise levels. Therefore, these other SCA methods, too, could potentially benefit from block-specific noise estimations on the basis of maximum likelihood extensions as discussed in the present paper. Following such an approach, the a priori fairness correction could be blended with block-specific noise estimations.
SCA-P assumes that the noise levels are equal for all data blocks. Often, this assumption does not match with situations encountered in practice. MxLSCA-P addresses this problem by allowing for different noise levels per data block, and by only requiring that the noise levels within each data block are equally and independently normal distributed. Yet, it is possible that noise levels also vary within a data block. For example, in addition to the fact that different measurement platforms can have different levels of reproducibility on average, within a measurement platform some variables could be measured more or less reliably than others (e.g., because of their chemical properties). This example illustrates that MxLSCA-P could benefit from allowing more complex 'within data block' error variance structures. Such complex variance structures could be incorporated following, for instance, a generalized least squares approach [26, 27].
Research within the functional genomics field is not only limited to static experiments, experiments in which samples are obtained in time are also often conducted (e.g., [28, 29]). To discover time-related effects in the data, MxLSCA-P could be extended using functional data analysis approaches [30].
Sometimes, the data sets collected in functional genomics studies are incomplete and contain missing data entries, for instance, due to experimental complications. The MxLSCA-P method could be extended to handle data sets containing missing values. For this, strategies like criss-cross regression [31, 32] could be adapted.
Conclusion
MxLSCA-P is a promising addition to the SCA family. Its ability to take different noise levels per data block into consideration and improve the recovery of the true patterns underlying the data could be beneficial for the analysis of coupled data blocks originating from different functional genomics sources. Moreover, the maximum likelihood based approach to SCA offers room for further extensions to allow for custom-made solutions to specific problems encountered in functional genomics research.
Methods
Metabolomics data
The metabolomics data set consisted of E. coli metabolomes (E. coli NST 74, a phenylalanine overproducing strain, and E. coli W3110, the wild-type strain). The E. coli strains were grown under different experimental conditions as described elsewhere [20]. The samples were analyzed by GC/MS and [33] and LC/MS [34]. The GC/MS and LC/MS samples were measured in duplicate. The final data blocks were manually cleaned up, removing spurious and double entries. After averaging of the duplicate measurements the data consisted of 28 experiments, 131 metabolites measured by GC/MS, and 44 metabolites measured by LC/MS. The metabolite data were autoscaled before analysis with SCA-P and MxLSCA-P. After autoscaling, each variable had mean zero and standard deviation one.
Simulation study
Experimental design
A full factorial design was developed for the simulation study. Each cell of the experimental design was independently repeated 20 times. The design consisted of the following factors:
-
The first factor is 'Method' with the two levels referring to the two different methods, SCA-P and MxLSCA-P.
-
The second factor is 'NoiseX1'. This factor determines the amount of noise on
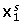 , the first simulated data block (see (11)). The levels of this factor are 10-3, 6.67, and 13.33% of noise variation of the total variation of
, the first simulated data block (see (11)). The levels of this factor are 10-3, 6.67, and 13.33% of noise variation of the total variation of 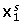 block. The specific percentages were chosen to simplify the conversion of data block noise levels into the factor 'Noise Total' (see below).
block. The specific percentages were chosen to simplify the conversion of data block noise levels into the factor 'Noise Total' (see below). -
The third factor is 'NoiseX2'. This factor determines the amount of noise on
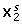 and has the same levels as the factor 'NoiseX1' now pertaining to X2.
and has the same levels as the factor 'NoiseX1' now pertaining to X2. -
The fourth factor is 'Number of variables' per X block. The first and second number indicates the number of variables of
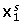 and
and 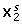 , respectively. The levels are '100 - 10', '70 - 20', and '40 - 30'.
, respectively. The levels are '100 - 10', '70 - 20', and '40 - 30'. -
The fifth factor is the factor 'Singular value' and its three levels are '4, 2 & 2, 1'; '2, 1 & 2, 1'; and '2, 1 & 4, 2'. The first two values become the singular values of
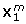 , the true X1 data block, and the second two become those of
, the true X1 data block, and the second two become those of 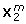 . Thus, for the first level of this factor,
. Thus, for the first level of this factor, 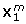 receives singular values 4 and 2, and
receives singular values 4 and 2, and 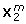 2 and 1. Note that these singular values are scaled to correct for the number of variables in each block before they become the final singular values of the X block (see section Data generation).
2 and 1. Note that these singular values are scaled to correct for the number of variables in each block before they become the final singular values of the X block (see section Data generation).
To improve the interpretation of the effect of different noise levels on the recovery of the true underlying data structures, the noise factors of the experimental design were converted into a 'noise ratio between data blocks (Noise Ratio)' and a 'sum of the noise levels (Noise Total)' factor. These factors were not part of the simulation, but were used instead of the factors 'NoiseX1' and 'NoiseX2' as independent variables in the ANOVA:
-
The Noise Ratio between data blocks factor consisted of three levels:
NoiseX1 < NoiseX2, Equal, and NoiseX1 > NoiseX2.
-
The Noise Total factor consisted of 'Low', 'Medium', and 'High' noise levels over all the blocks. In this study, 'Medium' was equal to NoiseX1 + NoiseX2 = 13.33. The sum of the noise levels smaller than 13.33 was 'Low', and larger was 'High'.
These converted factors remained orthogonal to the other design factors and to each other.
Data generation
Generation of the data blocks under the experimental design relied on Equation (11)

where 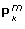 and
and  are generated under the design factors, and the matrix
are generated under the design factors, and the matrix  refers to the kth simulated data block. The true model parameters are indicated by 'm'. For completeness, the true data block
refers to the kth simulated data block. The true model parameters are indicated by 'm'. For completeness, the true data block  is given by
is given by  . The simulation study was performed in Matlab R2008a (the Mathworks).
. The simulation study was performed in Matlab R2008a (the Mathworks).
The true loading matrices  and
and  were generated based on the correlation matrices of the real life metabolomics data blocks. The data block obtained by GC/MS consisted of more variables than the LC/MS data block. Therefore, the GC/MS data block was used in the generation of the loadings for the largest data block in this simulation,
were generated based on the correlation matrices of the real life metabolomics data blocks. The data block obtained by GC/MS consisted of more variables than the LC/MS data block. Therefore, the GC/MS data block was used in the generation of the loadings for the largest data block in this simulation,  , and the LC/MS data block was used for the generation of
, and the LC/MS data block was used for the generation of  . The following procedure was followed in each simulation for the generation of the loadings:
. The following procedure was followed in each simulation for the generation of the loadings:
-
Randomly select J k variables from
 . The label 'real' indicates that these variables pertain to the real life measurements. The number of variables J
k
was given by the relevant design factor. Note that care was taken that J
k
is sufficiently smaller than
. The label 'real' indicates that these variables pertain to the real life measurements. The number of variables J
k
was given by the relevant design factor. Note that care was taken that J
k
is sufficiently smaller than  to ensure the subset of selected variables was sufficiently different in each simulation.
to ensure the subset of selected variables was sufficiently different in each simulation. -
Calculate the correlation matrix
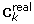 (J
k
× J
k
)
(J
k
× J
k
) -
Extract two normalized singular vectors belonging to the two largest singular values of
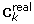 . These two vectors form
. These two vectors form 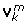 (J
k
× 2).
(J
k
× 2). -
Obtain the diagonal matrix
 (2 × 2) based on the factor 'Singular value'. Scale
(2 × 2) based on the factor 'Singular value'. Scale  by multiplying
by multiplying  by
by 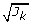 to correct for differences in block size.
to correct for differences in block size. -
Obtain the true loading matrix
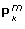 (J
k
× 2) by multiplication of
(J
k
× 2) by multiplication of 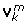 with
with  :
: 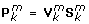 .
.
For each simulation, the true score matrix Tm(20 × 2) were obtained from the left singular vectors of a centered matrix of which the elements were independently drawn from a standard normal distribution. The elements of the noise matrix  (20 × J
k
) were each simulation obtained by independently drawing values from N(0,
(20 × J
k
) were each simulation obtained by independently drawing values from N(0,  ). The variance parameter
). The variance parameter  was set such that the expected variation of
was set such that the expected variation of  was a certain percentage of the total variation. This percentage was given by the design factors NoiseX1 and NoiseX2 for respectively the largest and smallest data block.
was a certain percentage of the total variation. This percentage was given by the design factors NoiseX1 and NoiseX2 for respectively the largest and smallest data block.
Recovery of the true data structures
As performance measure for the different methods, the recovery of the true component matrices Tmand 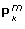 and the true data blocks
and the true data blocks  from the simulated data block
from the simulated data block  by the different SCA methods was determined. The closer the estimation of the components resembled the true component matrices, the better a method performs. The recovery of the data structures was measured by the modified RV coefficient [18], a matrix correlation measure, as a goodness of recovery measure. The range of modified RV coefficient is between -1 and 1 and '1' means perfect recovery. The modified RV coefficient is insensitive to orthogonal rotations, therefore we expect values close to 1. The modified RV coefficients were transformed using the Fisher-Z transformation to allow for values on the entire real line instead of between -1 and 1, thus a larger number indicates a better recovery. The transformed values are referred to as RV-Z. The recovery of the true data blocks
by the different SCA methods was determined. The closer the estimation of the components resembled the true component matrices, the better a method performs. The recovery of the data structures was measured by the modified RV coefficient [18], a matrix correlation measure, as a goodness of recovery measure. The range of modified RV coefficient is between -1 and 1 and '1' means perfect recovery. The modified RV coefficient is insensitive to orthogonal rotations, therefore we expect values close to 1. The modified RV coefficients were transformed using the Fisher-Z transformation to allow for values on the entire real line instead of between -1 and 1, thus a larger number indicates a better recovery. The transformed values are referred to as RV-Z. The recovery of the true data blocks  was also analyzed by the sum of squared differences per data block. This different recovery measure did not change the conclusions of this paper. Therefore, the RV-Z measure was used as a recovery measure for all data structures. The recovery measures obtained from the simulation study were analyzed by ANOVA using the GLM procedure of the software package SAS 9.2 (SAS). All factors were considered fixed for the ANOVA.
was also analyzed by the sum of squared differences per data block. This different recovery measure did not change the conclusions of this paper. Therefore, the RV-Z measure was used as a recovery measure for all data structures. The recovery measures obtained from the simulation study were analyzed by ANOVA using the GLM procedure of the software package SAS 9.2 (SAS). All factors were considered fixed for the ANOVA.
References
Ishii N, Nakahigashi K, Baba T, Robert M, Soga T, Kanai A, Hirasawa T, Naba M, Hirai K, Hoque A, Ho PY, Kakazu Y, Sugawara K, Igarashi S, Harada S, Masuda T, Sugiyama N, Togashi T, Hasegawa M, Takai Y, Yugi K, Arakawa K, Iwata N, Toya Y, Nakayama Y, Nishioka T, Shimizu K, Mori H, Tomita M: Multiple High-Throughput Analyses Monitor the Response of E. coli to Perturbations. Science 2007, 316(5824):593–597. 10.1126/science.1132067
Hirai MY, Yano M, Goodenowe DB, Kanaya S, Kimura T, Awazuhara M, Arita M, Fujiwara T, Saito K: Integration of transcriptomics and metabolomics for understanding of global responses to nutritional stresses in Arabidopsis thaliana . Proc Natl Acad Sci USA 2004, 101(27):10205–10210. 10.1073/pnas.0403218101
Bradley PH, Brauer MJ, Rabinowitz JD, Troyanskaya OG: Coordinated Concentration Changes of Transcripts and Metabolites in Saccharomyces cerevisiae . PLoS Comput Biol 2009, 5: e1000270. 10.1371/journal.pcbi.1000270
Yu H, Luscombe NM, Qian J, Gerstein M: Genomic analysis of gene expression relationships in transcriptional regulatory networks. Trends Genet 2003, 19(8):422–427. 10.1016/S0168-9525(03)00175-6
Lemmens K, Dhollander T, De Bie T, Monsieurs P, Engelen K, Smets B, Winderickx J, De Moor B, Marchal K: Inferring transcriptional modules from ChIP-chip, motif and microarray data. Genome Biol 2006, 7(5):R37. 10.1186/gb-2006-7-5-r37
Kiers HAL, ten Berge JMF: Hierarchical relations between methods for simultaneous component analysis and a technique for rotation to a simple simultaneous structure. Br J Math Stat Psychol 1994, 47: 109–126.
Timmerman ME, Kiers HAL: Four simultaneous component models for the analysis of multivariate time series from more than one subject to model intraindividual and interindividual differences. Psychometrika 2003, 68: 105–121. 10.1007/BF02296656
Bro R, Smilde AK: Centering and scaling in component analysis. J Chemom 2003, 17: 16–33. 10.1002/cem.773
van den Berg RA, Hoefsloot HCJ, Westerhuis JA, Smilde AK, van der Werf MJ: Centering, scaling, and transformations: improving the biological information content of metabolomics data. BMC Genomics 2006, 7: 142. 10.1186/1471-2164-7-142
Van Deun K, Smilde AK, Werf MJ, Kiers HAL, Van Mechelen I: A structured overview of simultaneous component based data integration. BMC Bioinformatics 2009, 10: 246. 10.1186/1471-2105-10-246
Kiers HAL: Towards a standardized notation and terminology in multiway analysis. J Chemom 2000, 14(3):105–122. Publisher Full Text 10.1002/1099-128X(200005/06)14:3<105::AID-CEM582>3.0.CO;2-I
Smilde AK, Westerhuis JA, de Jong S: A framework for sequential multiblock component methods. J Chemom 2003, 17: 323–337. 10.1002/cem.811
Wilderjans TF, Ceulemans E, Van Mechelen I: Simultaneous analysis of coupled data blocks differing in size: A comparison of two weighting schemes. Comput Stat Data An 2009, 53(4):1086–1098. 10.1016/j.csda.2008.09.031
Carroll J, Chang JJ: Analysis of individual differences in multidimensional scaling via an n-way generalization of 'Eckart-Young' decomposition. Psychometrika 1970, 35(3):283–319. 10.1007/BF02310791
Kroonenberg P, de Leeuw J: Principal component analysis of three-mode data by means of alternating least squares algorithms. Psychometrika 1980, 45: 69–97. 10.1007/BF02293599
Kiers HAL, Smilde AK: A comparison of various methods for multivariate regression with highly collinear variables. Stat Methods Appl 2007, 16(2):193–228. 10.1007/s10260-006-0025-5
Eilers PHC, Boer JM, van Ommen GJ, van Houwelingen HC: Classification of microarray data with penalized logistic regression. Proceedings of SPIE 2001, 4266: 187–198. 10.1117/12.427987
Smilde AK, Kiers HAL, Bijlsma S, Rubingh CM, van Erk MJ: Matrix correlations for high-dimensional data: the modified RV-coefficient. Bioinformatics 2009, 25(3):401–405. 10.1093/bioinformatics/btn634
van der Werf MJ, Overkamp KM, Muilwijk B, Coulier L, Hankemeier T: Microbial metabolomics: Toward a platform with full metabolome coverage. Anal Biochem 2007, 370: 17–25. 10.1016/j.ab.2007.07.022
Smilde AK, van der Werf MJ, Bijlsma S, van der Werff-van der Vat BJC, Jellema RH: Fusion of mass-spectrometry-based metabolomics data. Anal Chem 2005, 77(20):6729–6736. 10.1021/ac051080y
van Heijenoort J: Recent advances in the formation of the bacterial peptidoglycan monomer unit. Nat Prod Rep 2001, 18: 503–519. 10.1039/a804532a
Keseler IM, Vides JC, Castro SG, Ingraham JL, Paley S, Paulsen IT, Gil MP, Karp PD: a comprehensive database resource for Escherichia coli. Nucleic Acids Res 2005, 33(suppl_1):D334-D337.
Bos MP, Robert V, Tommassen J: Biogenesis of the gram-negative bacterial outer membrane. Annu Rev Microbiol 2007, 61: 191–214. 10.1146/annurev.micro.61.080706.093245
Pagès J: Collection and analysis of perceived product inter-distances using multiple factor analysis: Application to the study of 10 white wines from the Loire Valley. Food Qual Pref 2005, 16(7):642–649. 10.1016/j.foodqual.2005.01.006
de Tayrac M, Le S, Aubry M, Mosser J, Husson F: Simultaneous analysis of distinct Omics data sets with integration of biological knowledge: Multiple Factor Analysis approach. BMC Genomics 2009, 10: 32. 10.1186/1471-2164-10-32
Bro R, Sidiropoulos ND, Smilde AK: Maximum likelihood fitting using ordinary least squares algorithms. J Chemom 2002, 16: 387–400. 10.1002/cem.734
Johnston J, DiNardo J: Econometric Methods. 4th edition. New York: McGraw Hill Higher Education; 1997. [978–0071259644] [978-0071259644]
Rubingh CM, Bijlsma S, Jellema RH, Overkamp KM, van der Werf MJ, Smilde AK: Analyzing Longitudinal Microbial Metabolomics Data. J Proteome Res 2009, 8(9):4319–4327. 10.1021/pr900126e
Blanchard JL, Wholey WY, Conlon EM, Pomposiello PJ: Rapid Changes in Gene Expression Dynamics in Response to Superoxide Reveal SoxRS-Dependent and Independent Transcriptional Networks. PLoS ONE 2007, 2(11):e1186. 10.1371/journal.pone.0001186
Ramsay J, Silverman BW: Functional Data Analysis. 2nd edition. New York: Springer; 2005. [ISBN-10: 038740080X] [ISBN-10: 038740080X]
Kiers HAL: Weighted least squares fitting using ordinary least squares algorithms. Psychometrika 1997, 62(2):251–266. 10.1007/BF02295279
Gabriel KR, Zamir S: Lower Rank Approximation of Matrices by Least Squares with Any Choice of Weights. Technometrics 1979, 21(4):489–498. 10.2307/1268288
Koek M, Muilwijk B, van der Werf MJ, Hankemeier T: Microbial metabolomics with gas chromatography mass spectrometry. Anal Chem 2006, 78(4):1272–1281. 10.1021/ac051683+
Coulier L, Bas R, Jespersen S, Verheij E, van der Werf MJ, Hankemeier T: Simultaneous Quantitative Analysis of Metabolites Using Ion-Pair Liquid Chromatography-Electrospray Ionization Mass Spectrometry. Anal Chem 2006, 78(18):6573–6582. 10.1021/ac0607616
Acknowledgements
The authors would like to thank Dr. Mariët van der Werf (TNO Quality of Life, the Netherlands) for providing the E. coli metabolomics data set. We would also like to thank Dr. David Magis for interesting discussions. This work was supported by the Research Fund of the Katholieke Universiteit Leuven (EF/05/007 SymBioSys) and by IWT-Flanders (IWT/060045/SBO Bioframe).
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
RVDB performed the simulations, the analysis of the metabolomics data, and the writing of the manuscript. IVM recognized the usability of MxLSCA-P for the analysis of functional genomics data and aided the interpretation of the results and the writing of manuscript. TFW provided useful suggestions for the setup of the simulation study and the interpretation of the results. KVD provided useful suggestions for the setup of the simulation study, the ANOVA, the interpretation of the results, and the writing of the manuscript. HALK and AKS provided useful suggestions for the interpretation of the results. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is published under license to BioMed Central Ltd. This is an Open Access article is distributed under the terms of the Creative Commons Attribution License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
van den Berg, R.A., Van Mechelen, I., Wilderjans, T.F. et al. Integrating functional genomics data using maximum likelihood based simultaneous component analysis. BMC Bioinformatics 10, 340 (2009). https://doi.org/10.1186/1471-2105-10-340
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2105-10-340
 .
.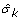 of σ
k
are calculated conditional on the previous estimations of
of σ
k
are calculated conditional on the previous estimations of  and
and 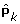 :
: 



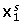 , the first simulated data block (see (11)). The levels of this factor are 10-3, 6.67, and 13.33% of noise variation of the total variation of
, the first simulated data block (see (11)). The levels of this factor are 10-3, 6.67, and 13.33% of noise variation of the total variation of 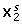 and has the same levels as the factor 'NoiseX1' now pertaining to X2.
and has the same levels as the factor 'NoiseX1' now pertaining to X2. . The label 'real' indicates that these variables pertain to the real life measurements. The number of variables J
k
was given by the relevant design factor. Note that care was taken that J
k
is sufficiently smaller than
. The label 'real' indicates that these variables pertain to the real life measurements. The number of variables J
k
was given by the relevant design factor. Note that care was taken that J
k
is sufficiently smaller than  to ensure the subset of selected variables was sufficiently different in each simulation.
to ensure the subset of selected variables was sufficiently different in each simulation.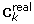 (J
k
× J
k
)
(J
k
× J
k
)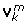 (J
k
× 2).
(J
k
× 2). (2 × 2) based on the factor 'Singular value'. Scale
(2 × 2) based on the factor 'Singular value'. Scale 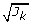 to correct for differences in block size.
to correct for differences in block size.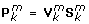 .
.