- Research article
- Open access
- Published:
A close examination of double filtering with fold change and t test in microarray analysis
BMC Bioinformatics volume 10, Article number: 402 (2009)
Abstract
Background
Many researchers use the double filtering procedure with fold change and t test to identify differentially expressed genes, in the hope that the double filtering will provide extra confidence in the results. Due to its simplicity, the double filtering procedure has been popular with applied researchers despite the development of more sophisticated methods.
Results
This paper, for the first time to our knowledge, provides theoretical insight on the drawback of the double filtering procedure. We show that fold change assumes all genes to have a common variance while t statistic assumes gene-specific variances. The two statistics are based on contradicting assumptions. Under the assumption that gene variances arise from a mixture of a common variance and gene-specific variances, we develop the theoretically most powerful likelihood ratio test statistic. We further demonstrate that the posterior inference based on a Bayesian mixture model and the widely used significance analysis of microarrays (SAM) statistic are better approximations to the likelihood ratio test than the double filtering procedure.
Conclusion
We demonstrate through hypothesis testing theory, simulation studies and real data examples, that well constructed shrinkage testing methods, which can be united under the mixture gene variance assumption, can considerably outperform the double filtering procedure.
Background
With the development of microarray technologies, researchers now can measure the relative expressions of tens of thousands of genes simultaneously. However, the number of replicates per gene is usually small, far less than the number of genes. Many statistical methods have been developed to identify differentially expressed (DE) genes. The use of fold change is among the first practice. It can be inefficient and erroneous because of the additional uncertainty induced by dividing two intensity values. There are variants of Student's t test procedure that conduct a test on each individual gene and then correct for multiple comparisons. The problem is, with a large number of tests and a small number of replicates per gene, the statistics are very unstable. For example, a large t statistic might arise because of an extremely small variance, even with a minor difference in the expression.
The disadvantage of fold-change approach and t test has been pointed out by a number of authors [1, 2]. There are approaches proposed to improve estimation of gene variances by borrowing strength across genes [1, 3, 4]. Despite the flaw, fold change and t test are the most intuitive approaches and they have been applied widely in practice. To control the error rate, many researchers use fold change and t test together, hoping that the double filtering will provide extra confidence in the test results. Specifically, a gene is flagged as DE only if the p-value from t test is smaller than a certain threshold and the fold change is greater than a cutoff value. For example, in [5], 90 genes were found to be DE with two cutoff values (p-value < 0.01 and fold change > 1.5). There are numerous examples in the literature that implement the double filtering procedure with fold change and t statistic [6–9]. We argue, however, that the double filtering procedure provides higher confidence mainly because it produces a shorter list of selected genes. Given the same number of genes selected, a well constructed shrinkage test can significantly outperform the double filtering method.
Fold change takes the ratio of a gene's average expression levels under two conditions. It is usually calculated as the difference on the log2 scale. Let x
ij
be the log-transformed expression measurement of the i th gene on the j th array under the control (i = 1,⋯, n and j = 1,⋯, m0), and y
ik
be the log-transformed expression measurement of the i th gene on the k th array under the treatment (k = 1,⋯m1). We define  and
and  .
.
Fold change is computed by

As for the traditional t test, it is usually calculated on the log2 scale to adjust for the skewness in the original gene expression measurements. The t statistic is then computed by

where  is the pooled variance of x
ij
and y
ik
. Comparing (1) and (2), it is obvious that fold change and t statistic are based on two contradicting assumptions. The underlying assumption of fold change is that all genes share a common variance (on the log2 scale), which is implied by the omission of the variance component in (1). On the other hand, the inclusion of
is the pooled variance of x
ij
and y
ik
. Comparing (1) and (2), it is obvious that fold change and t statistic are based on two contradicting assumptions. The underlying assumption of fold change is that all genes share a common variance (on the log2 scale), which is implied by the omission of the variance component in (1). On the other hand, the inclusion of  in (2) suggests that t test assumes gene-specific variances. In order for a gene to be flagged as DE, the double filtering procedure would require the gene to have extreme test scores under the common variance assumption as well as under the gene-specific variance assumption. It is analogous to using the intersection of the rejection regions defined by fold change and t statistic.
in (2) suggests that t test assumes gene-specific variances. In order for a gene to be flagged as DE, the double filtering procedure would require the gene to have extreme test scores under the common variance assumption as well as under the gene-specific variance assumption. It is analogous to using the intersection of the rejection regions defined by fold change and t statistic.
Assuming a common variance for all the genes apparently is an oversimplification. The assumption of gene-specific variances, however, leads to unstable estimates due to limited replicates from each gene. A more realistic assumption might lie in between the two extremes, i.e., modeling gene variances by a mixture of two components, one being a point mass at the common variance, another being a continuous distribution for the gene-specific variances. Under this mixture variance assumption, a DE gene could have a large fold change or a large t statistic, but not necessarily both. Taking intersection of the rejection regions flagged by fold change and t statistic, as is adopted by the double filtering procedure, might not be the best strategy under the mixture variance assumption.
The goal of the paper is not to propose a new testing procedure in microarray analysis, but to provide insight on the drawback of the widely used double filtering procedure with fold change and t test. We present a theoretically most powerful likelihood ratio (LR) test under the mixture variance assumption. We further demonstrate that two shrinkage test statistics, one from the Bayesian model [10] and the other from the significance analysis of microarrays (SAM) test [1], can be united as approximations to the LR test. This association explains why those shrinkage methods can considerably outperform the double filtering procedure. A simulation study and real microarray data analyses are then presented to compare the shrinkage tests and the double filtering procedure.
Methods
A Likelihood Ratio Test
For gene i, we use f
i
= p
v
fi 1+ (1 - p
v
)fi 2, a mixture of two components fi 1and fi 2, to denote the density under the null hypothesis that the gene is not DE under two experiment conditions. Density fi 1is defined under the gene-specific variance assumption, fi 2is defined under the common variance assumption, and p
v
is the mixing probability. Similarly, we use g
i
= p
v
gi 1+ (1 - p
v
)gi 2to denote the density under the alternative hypothesis, with gi 1and gi 2defined in a similar fashion as fi 1and fi 2. For example, in the context of testing DE genes, we can assume fi 1= N (μ
i
,  ), fi 2= N(μ
i
,
), fi 2= N(μ
i
,  ), gi 1= N(μ
i
+ Δ
i
,
), gi 1= N(μ
i
+ Δ
i
,  ), and gi 2= N(μ
i
+ Δ
i
,
), and gi 2= N(μ
i
+ Δ
i
,  ), where
), where  is the assumed common variance,
is the assumed common variance,  is the gene-specific variance, μ
i
is the mean expression level under the control, and Δ
i
is the difference in the expression levels between two conditions. Under the null hypothesis H0 : Δ
i
= 0, the likelihood ratio test statistic, which is the most powerful among all test statistics, is
is the gene-specific variance, μ
i
is the mean expression level under the control, and Δ
i
is the difference in the expression levels between two conditions. Under the null hypothesis H0 : Δ
i
= 0, the likelihood ratio test statistic, which is the most powerful among all test statistics, is

The R i statistic is a weighted sum of two ratios gi 1/fi 1and gi 2/fi 2, with weight w i = p v fi 1/[p v fi 1+ (1 - p v )fi 2]. Under the normality assumption, it is easy to show that R i = w i h1(|t i |) + (1 - w i )h2(|fc i |), where fc i and t i are fold change and t statistic, as defined in (1) and (2). Both h1(·) and h2(·) are monotonic increasing functions.
The rejection region of the LR test is defined by R i > λ R , where λ R is the threshold to attain a certain test size. In order to reject H0, it requires that either |fc i | is large, or |t i | is large, or both. In this sense, the LR test rejection region is more like a union of the rejection regions defined by fold change and t statistic. On the other hand, the double filtering procedure with fold change and t statistic would require both |fc i | and |t i | to be large. This practice is analogous to using the intersection of the two rejections regions determined by |fc i | and |t i |. Compared with the LR test, the double filtering procedure will lose power. The "loss of power" has two meanings. First, for a given false discovery rate (FDR), the double filtering procedure produces a shorter list of identified genes for further investigation. Second, for a given number of identified genes, the list produced by the double filtering procedure has a higher FDR. The double filtering procedure offers a false sense of confidence by producing a shorter list.
The LR test statistic R
i
requires one to know the true values of parameters p, μ
i
,  ,
,  , and Δ
i
, which are usually unknown in reality. One strategy is to estimate R
i
by
, and Δ
i
, which are usually unknown in reality. One strategy is to estimate R
i
by  , where the maximum likelihood estimates (MLE) of the unknown parameters are plugged into (3). Unfortunately, with a small number of replicates from each gene, the MLE would be extremely unstable and lead to unsatisfactory testing results.
, where the maximum likelihood estimates (MLE) of the unknown parameters are plugged into (3). Unfortunately, with a small number of replicates from each gene, the MLE would be extremely unstable and lead to unsatisfactory testing results.
A Bayesian model [10] was constructed under the mixture variance assumption to detect DE genes. The inference is made based on the marginal posterior probability of a gene being DE, denoted by z
i
= P(Δ
i
≠ 0 | X, Y). Here X = {x
ij
} and Y = {y
ik
} are the collection of gene expression data under the two conditions. We will show that, like  , z
i
is also an approximation to R
i
. The difference between
, z
i
is also an approximation to R
i
. The difference between  and z
i
is that the former plugs in the point estimates (MLE) of unknown parameters, while the latter marginalizes the unknown parameters with respect to their posterior distribution. In the Bayesian inference, the uncertainty from various sources are accounted for in a probabilistic fashion.
and z
i
is that the former plugs in the point estimates (MLE) of unknown parameters, while the latter marginalizes the unknown parameters with respect to their posterior distribution. In the Bayesian inference, the uncertainty from various sources are accounted for in a probabilistic fashion.
Similar to the Bayesian mixture model, some existing methods also try to strike a balance between the two extreme assumptions of a common variance and gene-specific variances. The SAM statistic slightly modifies the t-statistic by adding a constant to the estimated gene-specific standard deviation in the denominator. We will present it as being motivated by a mixture model on the variances (standard deviations). Furthermore, the SAM statistic can be directly written as a weighted sum of t statistic and fold change. Thus both the Bayesian method and the SAM method are approximations to the LR test under the mixture variance assumption, and they can achieve better performance than the double filtering procedure.
The Bayesian Mixture Model
Cao et al. [10] proposed a Bayesian mixture model to identify DE genes, which has shown comparable performance to frequentist shrinkage methods [1, 11]. With parameters (μ
i
, Δ
i
,  ,
,  , p
v
) defined similarly as in the LR test, gene expression measurements x
ij
and y
ij
are modeled by normal distributions with a mixture structure on the variances,
, p
v
) defined similarly as in the LR test, gene expression measurements x
ij
and y
ij
are modeled by normal distributions with a mixture structure on the variances,

A latent variable r i is used to model the expression status of the i th gene,,

where r
i
= 0/1 indicates that gene i is non-DE/DE and it is modeled by a Bernoulli distribution: r
i
| p
r
~ Bernoulli(p
r
). For  and
and  , it is assumed that
, it is assumed that  and
and  ~ IG(a0, b0). Here IG(a, b) denotes an inverse gamma distribution with mean b/(a - 1). The other hyper-priors include, μ
i
~ N(0,
~ IG(a0, b0). Here IG(a, b) denotes an inverse gamma distribution with mean b/(a - 1). The other hyper-priors include, μ
i
~ N(0,  ), p
r
~ U(0, 1), and p
v
~ U(0, 1). More details can be found in [10].
), p
r
~ U(0, 1), and p
v
~ U(0, 1). More details can be found in [10].
We make inference based on z i = P(r i = 1 | X, Y) = P(Δ i ≠ 0 | X, Y), the marginal posterior probability that gene i is DE. A gene is flagged as DE if z i > λ z , where λ z is a certain cutoff. We argue that the Bayesian rejection region defined by z i > λ z is an approximation to the LR test rejection region defined by R i > λ R . First we have

Here P(μ
i
, Δ
i
,  ,
,  , p
v
, p
r
| X, Y) is the joint posterior distribution of (μ
i
, Δ
i
,
, p
v
, p
r
| X, Y) is the joint posterior distribution of (μ
i
, Δ
i
,  ,
,  , p
v
, p
r
), marginalized with respect to other random parameters (e.g., μ
j
and
, p
v
, p
r
), marginalized with respect to other random parameters (e.g., μ
j
and  , j ≠ i).
, j ≠ i).
It is easy to show that

Given parameters (μ
i
, Δ
i
,  ,
,  , p
v
, p
r
), P(r
i
= 1 | μ
i
, Δ
i
,
, p
v
, p
r
), P(r
i
= 1 | μ
i
, Δ
i
,  ,
,  , p
v
, p
r
, X, Y) is an increasing function of R
i
. Rejecting H0 for R
i
> λ
R
is equivalent to rejecting for P(r
i
= 1 | λ
i
, Δ
i
,
, p
v
, p
r
, X, Y) is an increasing function of R
i
. Rejecting H0 for R
i
> λ
R
is equivalent to rejecting for P(r
i
= 1 | λ
i
, Δ
i
,  ,
,  , p
v
, p
r
, X, Y) > λ
z
, with λ
z
= λ
R
/[λ
R
+ (1 - p
r
)/p
r
]. Thus the two test statistics, P(r
i
= 1 | μ
i
, Δ
i
,
, p
v
, p
r
, X, Y) > λ
z
, with λ
z
= λ
R
/[λ
R
+ (1 - p
r
)/p
r
]. Thus the two test statistics, P(r
i
= 1 | μ
i
, Δ
i
,  ,
,  , p
v
, p
r
, X, Y) and R
i
, are equivalent. Expression (5) demonstrates that z
i
is obtained from P(r
i
= 1 | μ
i
, Δ
i
,
, p
v
, p
r
, X, Y) and R
i
, are equivalent. Expression (5) demonstrates that z
i
is obtained from P(r
i
= 1 | μ
i
, Δ
i
,  ,
,  , p
v
, p
r
, X, Y) by integrating with respect to the unknown parameters under the joint posterior distribution. If the integral does not have a closed form, we can conduct numerical integration to calculate z
i
through the Gibbs sampling algorithm [12, 13]. The uncertainty from those unknown parameters are accounted for in a probabilistic fashion. It is in this sense that we consider z
i
a good approximation to the LR test statistic R
i
.
, p
v
, p
r
, X, Y) by integrating with respect to the unknown parameters under the joint posterior distribution. If the integral does not have a closed form, we can conduct numerical integration to calculate z
i
through the Gibbs sampling algorithm [12, 13]. The uncertainty from those unknown parameters are accounted for in a probabilistic fashion. It is in this sense that we consider z
i
a good approximation to the LR test statistic R
i
.
The SAM Test
The SAM statistic [1] is defined as

where s
i
is the gene-specific standard deviation, and s0 is a constant that minimizes the coefficient of variation. Although it might not be the original intention of the authors [1], a test statistic like d
i
can be motivated by a model with a mixture structure on gene standard deviations. We begin with a simple case where x
ij
~ N(μ
i
,  ) and y
ik
~ N(μ
i
+ Δ
i
,
) and y
ik
~ N(μ
i
+ Δ
i
,  ), and the null hypothesis is H0 : Δ
i
= 0. Given δ
i
, the LR test statistic is
), and the null hypothesis is H0 : Δ
i
= 0. Given δ
i
, the LR test statistic is

We assume a mixture structure on gene standard deviations, where δ
i
= σ
i
with probability p
v
and δ
i
= σ0 with probability 1 - p
v
. We can then approximate  by
by

Replacing σ
i
with s
i
and  with s0, we can see that d
i
and
with s0, we can see that d
i
and  only differ by a factor of 1/p, which does not change the ordering of test statistics. The above derivation suggests that the SAM statistic can also be considered an approximation to the LR test statistic under the mixture variance (standard deviation) assumption. We can also write d
i
as a weighted sum of t
i
and fc
i
:
only differ by a factor of 1/p, which does not change the ordering of test statistics. The above derivation suggests that the SAM statistic can also be considered an approximation to the LR test statistic under the mixture variance (standard deviation) assumption. We can also write d
i
as a weighted sum of t
i
and fc
i
:

Recall that under the mixture variance assumption, the LR test statistic is R i = w i h1(|fc i |) + (1 - w i )h2(|t i |), where h1(·) and h2(·) are both monotonic increasing functions. Both d i and R i define rejection regions that are analogous to the union of the rejection regions defined by t test and fold change. In other words, the SAM procedure rejects H0 for large |t i |, or large |fc i |, or both. The SAM statistic is a better approximation to the LR test statistic than the double filtering procedure.
As a side note, Cui et al. [11] proposed a shrunken t test procedure based on a variance estimator that borrow information across genes using the James-Stein-Lindley shrinkage concept. This variance estimator shrinks individual variances toward a common value, which conceptually serves the same purpose as the mixture variance model. From this perspective, we also consider the shrunken t statistic an approximation to the LR test statistic.
Results and Discussion
Simulation Study
We conducted a simulation study to compare the double filtering procedure to the shrinkage methods. The simulation truth is specified as follows. We tested 1000 genes with 100 genes being truly DE. Without loss of generality, we set μ i = 0. We further assumed

and

Three scenarios were considered. Scenario 1: 90% of the genes with gene-specific variances and 10% of the genes with a common variance, and 3 replicates per gene under each condition. Scenario 2: same as Scenario 1, but with 6 replicates per gene under each condition. Scenario 3: all the genes having a gene-specific variance, and 3 replicates per gene under each condition. For each scenario we repeated the simulation 1000 times.
For the Bayesian mixture model, we specified noninformative priors so that the posterior inference is dominated by information from data. We let  =
=  = 5.0 where 5.0 is sufficiently large for expression levels on the logarithm scale. To specify the hyper-parameters for the inverse gamma priors, first we set a
σ
= a0 = 2.0 so that the inverse gamma priors have an infinite variance. Then we set the prior means,
= 5.0 where 5.0 is sufficiently large for expression levels on the logarithm scale. To specify the hyper-parameters for the inverse gamma priors, first we set a
σ
= a0 = 2.0 so that the inverse gamma priors have an infinite variance. Then we set the prior means,  and
and  , equal to the average of the sample variances to solve for b
σ
and b0. Finally, we chose a
r
= b
r
= a
v
= b
v
= 1, which corresponds to uniform priors for p
r
and p
v
.
, equal to the average of the sample variances to solve for b
σ
and b0. Finally, we chose a
r
= b
r
= a
v
= b
v
= 1, which corresponds to uniform priors for p
r
and p
v
.
Five test statistics were compared: the marginal posterior probability (z i ) of a gene being DE based on the Bayesian mixture model, the SAM statistic, the shrunken t statistic, the t statistic, and the double filtering with t statistic and fold change greater than 2. The first three graphs in Figure 1 plot the FDR versus the total number of selected genes under the above three scenarios. The shrinkage methods (the Bayesian model, the SAM test, and the shrunken t test) have comparable performance. The double filtering procedure performs better than the traditional t statistic, but it is obviously outperformed by the three shrinkage methods. We have tried different fold change cutoff values for the double filtering procedure (e.g., setting the cutoff at 1.5) and the results did not change materially. Given the same number of selected genes, the shrinkage methods can identify more truly DE genes than the double filtering procedure. Note that under the gene-specific variance assumption (Scenario 3), the t test, which theoretically is the most powerful likelihood ratio test, still performs the poorest. This result indicates the usefulness of shrinkage in microarray studies, where only a small number of replicates are available for each gene. In short, the simulation study shows that for a given number of selected genes, well constructed shrinkage methods can outperform the double filtering procedure.
Comparison of the FDR given the total number of selected genes under Scenario 1-6 in the simulation study. The competing test statistics are the posterior probability based on the Bayesian model, the shrunken t statistic, the SAM statistic, the t statistic, and the double filtering procedure with t statistic and fold change.
In Scenario 1 and 2 of the simulation study, the true variance distribution is specified as the mixture of a point mass and an inverse gamma distribution, which might lead to a result that is biased in favor of a shrinkage method. Here we conduct another simulation study with a "real" variance distribution, denoted as Scenario 4. Specifically, let x ij (j = 1, ... , m0i) and y ik (k = 1, ... , m1i) be the observed expression levels from a real microarray study.
Define the residual vector e
i
=(ei 1, ... ,  )' by
)' by

Then e i can be considered a set of random errors sampled based on the true variance distribution. We simulate 1000 data sets according to the following steps. For iteration s (s = 1, ⋯, 1000) and gene i (i = 1, ... , n),
-
1.
obtain a random permutation of (e i 1, ... ,
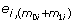 ), denoted by
), denoted by 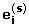 ;
; -
2.
generate
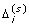 as described in the previous simulation scenarios;
as described in the previous simulation scenarios; -
3.
for j = 1, ... , m 0i, compute
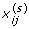 =
=  , and for k = 1, ... , m 1i, compute
, and for k = 1, ... , m 1i, compute 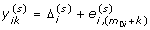 , where
, where  is the j th element of
is the j th element of 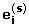 .
.
The real data comes from a microarray study comparing the gene expressions of breast cancer tumors with BRCA1 mutations, BRCA2 mutations, and sporadic tumors [14]. The data set is available at http://research.nhgri.nih.gov/microarray/NEJM_Supplement. Here we only consider the BRCA1 group and the BRCA2 group. There are 3226 genes, with 7 arrays in the BRCA1 group and 8 arrays in the BRCA2 group. We analyzed the data on the log2 scale. Following Storey and Tibshirani [15], we eliminated genes with aberrantly large expression values (>20), which left us with measurements on n = 3169 genes. The fourth graph in Figure 1 compares the different methods under Scenario 4, where the residual vector e i was constructed based on the breast cancer data. We kept the same replicate number in the experiment, with 7 replicates per gene in one group and 8 replicates in the other group. The relative performance of the five methods remains unchanged as in the other scenarios.
In current microarray studies, the number of replicates per gene can be easily 30 or more due to the low cost of array and the easiness to collect patients. So we considered two scenarios with a relatively large number of replicates. Scenario 5: 90% of the genes with gene-specific variances and 10% of the genes with a common variance, and 30 replicates per gene under each condition. Scenario 6: all the genes having a gene-specific variance, and 30 replicates per gene under each condition. In each of the two scenarios, we assume there are 1000 genes with 100 genes being truly DE. The two graphs in the bottom panel of Figure 1 plot the FDR versus the total number of selected genes for the five test statistics under Scenario 5 and Scenario 6, respectively. The comparison demonstrates that when the replicate number is large, the performance of the traditional t test becomes comparable to the performance of the shrinkage methods, thanks to the more reliable estimate of gene variance component. More importantly, the drawback of the double filtering procedure becomes more obvious, which has substantially worse performance compared to the other methods, including the t test.
Experimental Datasets
In this section we compared the shrinkage methods with the double filtering procedure based on two microarray datasets. The first is the Golden Spike data [16] where the identities of truly DE genes are known. The Golden Spike dataset includes two conditions, with 3 replicates per condition. Each array has 14,010 probesets, among which 10,144 have non-spiked-in RNAs, 2,535 have equal concentrations of RNAs, and 1,331 are spiked-in at different fold-change levels, ranging from 1.2 to 4-fold. Compared with other spike datasets, the Golden Spike dataset has a larger number of probsets that are known to be DE, making it popular for comparing performance among different methods. Irizarry et al. [17] pointed out that "the feature intensities for genes spiked-in to be at 1:1 ratios behave very differently from the features from non-spiked-in genes". Following Opgen-Rhein and Strimmer [18], we removed the 2,535 probe sets for spike-ins with ratio 1:1 from the original data, leaving in total 11,475 genes and 1,331 known DE genes. Figure 2 plots the FDR under each testing procedures versus the total number of rejections. For the double filtering procedure, the fold change cutoff was set at 1.5 because only 248 genes have a fold change greater than 2.0. The figure indicates that the shrinkage methods (Bayesian, SAM, and shrunken t) have similar performance, and they outperform the double filtering procedure and t test.
Comparison of the FDR given the total number of selected genes in the analysis of Golden Spike data. The test statistics include the posterior probability based on the Bayesian model, the shrunken t statistic, the SAM statistic, the t statistic, and the double filtering procedure with t statistic and fold change.
The second is the breast cancer dataset [14] described in the simulation study. With the identities of truly DE genes unknown, we estimated the FDR for the SAM test, the shrunken t test, the t test, and the double filtering procedure, through the permutation approach described in [15]. For Bayesian methods, Newton et al. [19] proposed to compute the Bayesian FDR, which is the posterior proportion of false positives relative to the total number of rejections. However, the Bayesian FDR is incomparable to the permutation-based FDR estimate employed by frequentist methods [20]. Cao and Zhang [21] developed a generic approach to estimating the FDR for Bayesian methods under the permutation-based framework. A computationally efficient algorithm was developed to approximate the null distribution of the Bayesian test statistic, the posterior probability. The approach can provide an unbiased estimate of the true FDR. Constructed under the same permutation-based framework, the resulting FDR estimate allows a fair comparison between full Bayesian methods with other testing procedures. We adopted the approach in [21] to estimate the FDR of the Bayesian mixture model (4). Figure 3 plots the permutation-based FDR estimates under each testing procedure versus the total number of rejections. It shows that the shrinkage methods can considerably outperform the double filtering procedure.
Comparison of the estimated FDR given the total number of selected genes in the analysis of the breast cancer data. The test statistics include the posterior probability based on the Bayesian model, the shrunken t statistic, the SAM statistic, the t statistic, and the double filtering procedure with t statistic and fold change.
Conclusion
It has been a common practice in microarray analysis to use fold change and t statistic to double filter DE genes. In this paper, we provided a close examination on the drawback of the double filtering procedure, where fold change and t statistic are based on contradicting assumptions. We further demonstrated that several shrinkage methods (SAM, shrunken t, and a Bayesian mixture model) can be united under the mixture gene variance assumption. Based on the theoretical derivation, the simulation study, and the real data analysis, we showed compelling evidence that well constructed shrinkage methods can outperform the double filtering procedure in identifying DE genes. With publicly available softwares, these methods are as easy to implement as the double filtering procedure.
We acknowledge some researchers' argument that the double filtering procedure might work well because it filters out the genes that show relatively small differences between conditions, which are sometimes considered to be less biologically meaningful. This argument, however, is based on the criterion of so called "biological meaningfulness" instead of testing power. Although many biologists refer to fold change in terms of "biological meaningfulness", there is in fact no clear cut-off for it, and 2-fold is often invoked merely based on convenience. In addition, different normalization methods can differ quite drastically in terms of the fold changes they produce. So a particular cut-off in fold change could mean one thing using one method and quite another using a different method. Taken together, even if researchers decide to employ the double filtering procedure based on the rationale of "biological meaningfulness", it is still helpful to understand the potential loss in power.
References
Tusher VG, Tibshirani R, Chu G: Significance analysis of microarrays applied to transcriptional responses to ionizing radiation. Proceedings of the National Academy of Sciences 2001, 98: 5116–5121. 10.1073/pnas.091062498
Jain N, Thatte J, Braciale T, Ley K, O'Connell M, Lee JK: Local-pooled-error test for identifying differentially expressed genes with a small number of replicated microarrays. Bioinformatics 2003, 19(15):1945–1951. 10.1093/bioinformatics/btg264
Baldi P, Long AD: A Bayesian framework for the analysis of microarray expression data: regularized t-test and statistical inference of gene changes. Bioinformatics 2001, 17: 509–519. 10.1093/bioinformatics/17.6.509
Lonnstedt I, Speed T: Replicated microarray data. Statistica Sinica 2002, 12: 31–46.
Han T, Wang J, Tong W, Moore MM, Fuscoe JC, Chen T: Microarray analysis distinguishes differential gene expression patterns from large and small colony Thymidine kinase mutants of L5178Y mouse lymphoma cells. BMC Bioinformatics 2006, 7(Suppl 2):S9. 10.1186/1471-2105-7-S2-S9
Kittleson MM, Minhas KM, Irizarry RA, Ye SQ, Edness G, Breton E, Conte JV, Tomaselli G, Garcia JGN, Hare JM: Gene expression in giant cell myocarditis: Altered expression of immune response genes. International Journal of Cardiology 2005, 102(2):333–340. 10.1016/j.ijcard.2005.03.075
Li Y, Elashoff D, Oh M, Sinha U, St John MAR, Zhou X, Abemayor E, Wong DT: Serum circulating human mRNA profiling and its utility for oral cancer detection. Journal of Clinical Oncology 2006, 24(11):1754–1760. 10.1200/JCO.2005.03.7598
Quinn P, Bowers RM, Zhang X, Wahlund TM, Fanelli MA, Olszova D, Read BA: cDNA microarrays as a tool for identification of biomineralization proteins in the coccolithophorid Emiliania hux-leyi (Haptophyta). Applied and Environmental Microbiology 2006, 72(8):5512–5526. 10.1128/AEM.00343-06
Sauer M, Jakob A, Nordheim A, Hochholdinger F: Proteomic analysis of shoot-borne root initiation in maize (Zea mays L.). Proteomics 2006, 6(8):2530–2541. 10.1002/pmic.200500564
Cao J, Xie X, Zhang S, Whitehurst A, White M: Bayesian optimal discovery procedure for simultaneous significance testing. BMC Bioinformatics 2009, 10: 5. 10.1186/1471-2105-10-5
Cui X, Hwang JTG, Qiu J, Blades NJ, Churchill GA: Improved statistical tests for differential gene expression by shrinking variance components estimates. Biostatistics 2005, 6: 59–75. 10.1093/biostatistics/kxh018
Gelfand AE, Smith AFM: Sampling-Based Approaches to Calculating Marginal Densities. Journal of the American Statistical Association 1990, 85(410):398–409. 10.2307/2289776
Casella G, George EI: Explaining the Gibbs sampler. The American Statistician 1992, 46(3):167–174. 10.2307/2685208
Hedenfalk I, Duggan D, Chen Y, Radmacher M, Bittner M, Simon R, Meltzer P, Gusterson B, Esteller M, Kallioniemi O, Wilfond B, Borg A, Trent J: Gene-expression profiles in hereditary breast cancer. New England Journal of Medicine 2002, 344(8):539–548. 10.1056/NEJM200102223440801
Storey JD, Tibshirani R: Statistical significance for genomewide studies. Proceedings of the National Academy of Sciences 2003, 100: 9440–9445. 10.1073/pnas.1530509100
Choe SE, Boutros M, Michelson AM, Church GM, Halfon MS: Preferred analysis methods for Affymetrix GeneChips revealed by a wholly defined control dataset. Genome Biology 2005, 6(2):R16. 10.1186/gb-2005-6-2-r16
Irizarry RA, Cope LM, Wu Z: Feature-level exploration of a published Affymetrix GeneChip control dataset. Genome Biology 2006, 7(8):404. 10.1186/gb-2006-7-8-404
Opgen-Rhein R, Strimmer K: Accurate ranking of differentially expressed genes by a distribution-free shrinkage approach. Statistical Applications in Genetics and Molecular Biology 2007, 6(1):9. 10.2202/1544-6115.1252
Newton MA, Noueiry A, Sarkar D, Ahlquist P: Detecting differential gene expression with a semiparametric hierarchical mixture method. Biostatistics 2004, 4: 155–176. 10.1093/biostatistics/5.2.155
Storey JD, Dai JY, Leek JT: The optimal discovery procedure for large-scale significance testing, with applications to comparative microarray experiments. Biostatistics 2007, 8: 414–432. 10.1093/biostatistics/kxl019
Cao J, Zhang S: Measuring statistical significance for full Bayesian methods in microarray analysis. Technical report [http://smu.edu/statistics/TechReports/tech-rpts.asp]
Acknowledgements
This work has been supported in part by the U.S. National Institutes of Health UL1 RR024982. The authors thank the reviewers for their constructive comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
SZ and JC conceived the study, conducted the examination on the double filtering procedure, analyzed the data, and drafted the paper. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, S., Cao, J. A close examination of double filtering with fold change and t test in microarray analysis. BMC Bioinformatics 10, 402 (2009). https://doi.org/10.1186/1471-2105-10-402
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2105-10-402

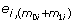 ), denoted by
), denoted by 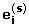 ;
;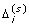 as described in the previous simulation scenarios;
as described in the previous simulation scenarios;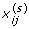 =
=  , and for k = 1, ... , m 1i, compute
, and for k = 1, ... , m 1i, compute 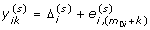 , where
, where 
