Given n strings s1, …, sn each of length ℓ and a nonnegative integer d, the CLOSEST STRING problem asks to find a center string s such that none of the input strings has Hamming distance greater than d from s. Finding a common pattern in many – but not necessarily all – input strings is an important task that plays a role in many applications in bioinformatics.
Results
Although the closest string model is robust to the oversampling of strings in the input, it is severely affected by the existence of outliers. We propose a refined model, the CLOSEST STRING WITH OUTLIERS (CSWO) problem, to overcome this limitation. This new model asks for a center string s that is within Hamming distance d to at least n – k of the n input strings, where k is a parameter describing the maximum number of outliers. A CSWO solution not only provides the center string as a representative for the set of strings but also reveals the outliers of the set.
We provide fixed parameter algorithms for CSWO when d and k are parameters, for both bounded and unbounded alphabets. We also show that when the alphabet is unbounded the problem is W[1]-hard with respect to n – k, ℓ, and d.
Conclusions
Our refined model abstractly models finding common patterns in several but not all input strings. We initialize the study of the computability of this model and show that it is sensitive to different parameterizations. Lastly, we conclude by suggesting several open problems which warrant further investigation.
Background
Finding similar regions in multiple DNA, RNA, or protein sequences plays an important role in many applications, including universal PCR primer design [1–4], genetic probe design [2], antisense drug design [2, 5], finding transcription factor binding sites in genomic data [6], determining an unbiased consensus of a protein family [7], and motif-recognition [2, 8, 9]. The CLOSEST STRING problem formalizes these tasks and can be defined as follows: given a set of n strings S of length ℓ over the alphabet Σ and parameter d, the aim is to determine if there exists a string s that has Hamming distance at most d from each string in S. The optimization version of this problem tries to minimize the parameter d. We refer to s as the center string and let d(x, y) be the Hamming distance between strings x and y.
The CLOSEST STRING was first introduced and studied in the context bioinformatics by Lanctot et al. [2]. Frances and Litman [10] showed the problem to be NP-complete even in the special case when the alphabet is binary, implying there is unlikely to be a polynomial-time algorithm for this problem unless P = NP. Since its introduction the investigation of efficient polynomial time approximation algorithms and exact exponential time algorithms for the CLOSEST STRING problem has been thoroughly considered [2, 11–16].
The CLOSEST STRING problem requires that the Hamming distance constraint be satisfied for each of the input strings and therefore, is robust to the oversampling of the input strings. For this reason it is frequently used to model many of the aforementioned applications. However, this property also causes a severe problem: if the input includes a string that is significantly different from the other input strings, which we refer to as an “outlier”, then it will have the effect of causing there not to exist a center string for the complete set of input strings; d will have to be increased dramatically to account for this string and obtain a center string. This is a significant limitation for applications such as the design of universal primers where a small d is crucial for the effectiveness of the primers. In this and many other applications, it would be preferable to determine a “good” center string (i.e. one that is reasonably close to each of the strings) for a large portion of the input strings rather than trying to find a center string for the complete set and in doing so finding one that is far distance from many or all of the strings. Hence, we aim to model the task of finding a center string that is within distance d to most – but not necessarily all – of the input strings, where d is reasonably small. Another compelling consequence of the modification of the model is that in situations where a more satisfying solution can be found by regarding a few strings as outliers, the initial decision of including them requires reexamination.
We formally model this problem as follows:
CLOSEST STRING WITH OUTLIERS (CSWO)
INPUT: A set of n length-ℓ strings S = {s1,…, sn} over a finite alphabet Σ and nonnegative integers k and d.
QUESTION: Find a center string s and a subset of S* ⊂S, such that |S*| = n – k and d(s, t) ≤ d for t∈S*.
For the rest of the paper we denote n – k as n*, and si [p] to be the symbol at position p of string si.
There exists a simple reduction from the CLOSEST STRING problem to CSWO that demonstrates it is NP-complete even in the special case where the alphabet is binary and k = 0, implying it is unlikely to be solved exactly by a polynomial-time algorithm, unless P=NP. One approach to investigating the computational intractability of CSWO is to consider its parameterized complexity, which aims to classify computationally hard problems according to their inherent difficulty with respect to multiple parameters of the input. If it is solvable by an algorithm that is polynomial in the input size and exponential in parameters that are typically small then it can still be considered tractable in some practical sense.
For unbounded alphabet size, we show that CSWO is W[1]-hard for every combination of the parameters ℓ, d, and n* and thus, is fixed parameter intractable when parameterized by any subset of these parameters, unless FPT = W[1]. We also show that when the alphabet is unbounded, there exists a fixed parameter tractable algorithm for CSWO with respect to the parameters d and k. In the case of constant size alphabet, CSWO is fixed parameter tractable for the parameter n but intractable for the parameter k. The complexity of the problem remains open when parameterized by d and the alphabet is of constant size, and when parameterized by n* and k.
Previous Results
It is worth noting that analogous parameterized complexity studies have been performed for the CLOSEST STRING problem and the CLOSEST SUBSTRING problem. Gramm et al. [13] demonstrated that the CLOSEST STRING problem is FPT when the number of strings remains fixed. This FPT result is based on an integer linear programming formulation with a constant number of variables (assuming n is fixed), and the application of the result of Lenstra [19] that proves integer linear programming is polynomial-time solvable when the number of variables remains fixed. They further demonstrated that the problem is FPT when d is a parameter by giving a O(n ℓ + nd(d + 1)d) time algorithm [13]. Ma and Sun gave an O(n|Σ|O(d)) algorithm, which is a polynomial-time algorithm when d = O(log n) and Σ has constant size [16]. Chen et al. [20], Wang and Zhu [21], and Zhao and Zhang [22] improved upon the fixed parameter tractable result of Ma and Sun [16].
The CLOSEST SUBSTRING problem seems to be inherently more intractable then the CLOSEST STRING problem. Given n strings s1, s2,…, sn over alphabet Σ and integers d and ℓ, the CLOSEST SUBSTRING problem aims to determine whether there is a string s of length ℓ such that, for all i = 1,…, n, d(s, ) ≤ d where is a length ℓ substring of si. Fellows et al. [11] showed that CLOSEST SUBSTRING is W[1]-hard with respect to the number of input strings n even for a binary alphabet. When Σ is unbounded the problem is W[1]-hard with respect to the parameters ℓ, d and n[11]. Most recently, Marx [23] proved the problem is W[1]-hard with combined parameters n and d even if the alphabet is binary, which resolved an open problem stated in [11, 12, 24].
Methods
We give insight into the computational tractability of CSWO through studying the parameterized complexity of the problem. Parameterized complexity aims to classify problems according to their inherent difficulty with respect to multiple parameters of the input.
Parameterized Complexity
A problem φ is said to be fixed parameter tractable with respect to parameter k if there exists an algorithm that solves φ in f(k) · nO(1) time, where f is a function of k that is independent of n[17]. Given a graph G = (V, E) with vertex set V, edge set E, and positive integer k, the Vertex Cover problem aims to discern where there is a subset of vertices Vc⊆V with k or fewer vertices such that each edge in E has at least one its endpoints in Vc . The vertex cover problem is NP-complete [18] but is fixed parameter tractable since there exists algorithmic solutions that have running time O(kn + 1.3k) [17]. The corresponding complexity class is FPT.
Not all NP-complete problems are in FPT. For example, consider the NP-complete CLIQUE problem: given an undirected graph G = (V, E) and a positive integer t, the aim is determine whether there is a subset of vertices C⊆V of size at least t where each pair of vertices in C are connected by an edge. The best known algorithms for solving clique runs in time O(no(t)) and hence, there is no known algorithm for solving t for which t is not in the exponent of n in the running time [17].
In order to characterize those problems that do not seem to admit a fixed parameter efficient algorithm, Downey and Fellows [17] defined a fixed parameter reduction. We will restrict interest to the W[1] class and hence, the following definition will only apply to W[1]-hardness. W[1]-hardness gives convincing evidence that a parameterized problem with parameter k is unlikely to have an algorithm that has running time of the form f(k) · nO(1). Let L, L′ ⊆ Σ* ×ℕ be two parameterized languages, then L reduces to L′ if there are functions k → k′ and k → k″ from ℕ to ℕ and a function (x, k) → x′ from Σ* ×ℕ to Σ* such that:
1.
(x, k) → x′ is computable in time k″|x|c, for some constant c and
2.
(x, k) ∈L if and only if (x′, k′) ∈L′.
Results and Discussion
In the following subsections, we study the parameterized tractability of CSWO and show the problem is sensitive to different parameterizations.
CSWO: Tractability Results
We first consider when Σ is a parameter. In computational biology applications the biological sequences of interest are typically DNA or protein sequences, hence the number of different symbols is a small constant (i.e. 4 or 20 in the case of DNA or protein sequences, respectively). Restricting Σ only does not make CSWO tractable since it is NP-hard even when the alphabet is binary. However, if Σ and ℓ are both parameters then it is fixed-parameter tractable; we can enumerate and check all the |Σ|ℓ possible center strings. As a result the problem is fixed parameter tractable with the combined parameters Σ, ℓ, d and n*. We will prove in a later section that it is imperative that Σ be a parameter in order to obtain this tractability.
Next we show that CSWO is fixed parameter tractable if d and k are parameters. The fixed parameter algorithm that we present is similar to the algorithm presented by Gramm et al. [13], where it is proved that CLOSEST STRING is fixed parameter tractable with respect to the parameter d. In the algorithm by Gramm et al. [13] at each recursive step a string s is selected that has Hamming distance at least d + 1 away from the current candidate center string x if one exists; otherwise x is returned since it is a center string. Then for any d + 1 positions where x and s disagree, there is at least one position at which s is equal to the final solution. The algorithm tries each of the d + 1 positions, changes x to s at one of the d + 1 the position, reduces Δd by one, and calls itself recursively. Hence, Δd is the current degeneracy parameter at a particular recursive iteration and x is the current candidate center string. Since the recursion stops after at most d steps the size of the search tree is bounded by O((d + 1)d).
CSWO Algorithm
Input: A CSWO instance with a set of S n strings of length ℓ, parameters Δd, d and k, and a candidate string x.
Output: A string s* if there exists a set S of at least n* strings where each string in S has distance at most d from s*, and “Not found” otherwise.
1.
If Δd < 0 or k < 0 then return “Not found”.
2.
Choose i∈ {1,…, n} such that d(x, si) > d. If no such i exists return x.
3.
sret = CSWO Algorithm (S\ {si}, Δd, k – 1, x).
4.
If sret = “not found ” then:
(a)
P = {p | x[p] ≠ si[p]};
(b)
Choose any P′ from P with |P′| = d + 1.
(c)
For each position p∈P′:
Let x be equal to si at position p.
sret = CSWO Algorithm (S, Δd – 1, k, x).
If sret ≠ “not found”, then return sret.
5.
Return “not found”.
Our algorithm begins with s1 as the candidate center string. If s1 is a center string with respect to S then we are done; otherwise there exists a string si that has distance at least d + 1 from s1. We “guess” whether si belongs in the set of outliers. If it is an outlier then we remove it from S and recurse on the smaller set with k – 1. If it is not an outlier then we use si to move the candidate string x closer to toward si, which can be done by applying the methodology of Gramm et al. [13]. We use the term “guess” as an euphemism in this brief description of the our algorithm but rather we try both possibilities as can be seen in the CSWO Algorithm. This will increase the size of the search tree.
Proposition 1The CSWO Algorithm solves the CSWO problem in time O(n ℓ + nd · dd· 2k+d).
Proof. Running time. Each recursion of the algorithm reduces either k or d by 1. Thus, there are at most k + d guesses of whether a particular string belongs in the set of outliers. Thus, the search tree size is increased by a multiplicative factor of at most 2k+d and the search tree size is bounded above by O(2k+d· (d + 1)d). The analysis of Gramm et al. [13] demonstrated that each recursive step takes time O(nd) and the preprocessing time takes O(n ℓ) and therefore, we obtain an overall running time of O(n ℓ + nd · dd· 2k+d).
Correctness We show the correctness of the algorithm by showing the correctness of the first recursive step and then the correctness of the algorithm follows by inductively applying the following argument. Clearly, if S does not contain a subset S* of n* strings, such that there exists a center string s* for S* then “not found” will be returned and therefore, we assume otherwise.
If s1 is a center string for S then the algorithm immediately halts so we assume there exists a string si in S that does not have s1 as a center string. CSWO Algorithm creates two subcases: one where si is in the set of outliers, and another where si is not. Suppose si is in the set of outliers then the first case will successfully remove si from the set and recurse on S\{si}. Otherwise, if si is not in the set of outliers then eventually the second case will reached. We refer to the set of positions as correct if {p | s1[p] ≠ s*[p] = s[p]}. It follows from Gramm et al. [13] that one of the d + 1 chosen positions p will be a correct one. Thus, we have shown that either one of the subcases will lead to a smaller subcase containing the solution for S.
The previous result demonstrates the fixed parameter tractability with respect to d and k. We note that a similar modification of the O(n|Σ|O(d)) algorithm of Ma and Sun [16] also gives a fixed parameter algorithm with respect to the parameters Σ, d and k. In the modified algorithm, for any string s with distance greater than d to the current candidate center string x, we again try the subcases where s is an outlier, and is not an outlier. In the former case, we remove s from the set of input strings S and recurse on S and k – 1, and in the latter case, we use the same technique as in the algorithm of Ma and Sun [16] to reduce the distance between x and the final solution. This modification that accounts for the outliers results an extra multiplicative factor of O(2k+logd) to the running time of the original algorithm. Although this algorithm improves upon the running time of the previous result, it requires that Σ is also a parameter. Further, we note that some of the recent improvements [20–22] to the algorithm of Ma and Sun can be modified in a similar manner to obtain fixed parameter algorithms for CSWO with respect to parameters Σ, d and k.
Proposition 2 CSWO is fixed parameter tractable for parameters Σ and n.
Proof. Gramm et al. [13] gave a linear fixed parameter tractable algorithm for CLOSEST STRING with respect to the number of strings and Σ, which we refer to this algorithm as ILP-procedure(S), where S is the set of input strings. Our algorithm enumerates all size-n* subsets of S, and call ILP-procedure on each subset.
CSWO: Intractability Results
We derive the W[1]-hardness result by a series of intermediate steps, aiming at a reduction from Clique to CSWO, showing that CSWO is W[1]-hard for the combination of ℓ, d, and n*, and when the alphabet is unbounded.
Reduction from CLIQUE
As previously described, we let the CLIQUE instance be given by an undirected graph G = (V, E) with a set V = {v1,v2,…,vn} of n vertices, a set E of m edges, and a positive integer t denoting the size of the desired clique. We describe how to generate a set S of strings such that G has a clique of size t if and only if there is a subset of S of size , denoted as S*, where there exists a string x such that d(si,x) ≤ d for all si∈S*. We let ℓ = t and d = t – 2. We assume that t > 2 since t ≤ 1 produces trivial cases.
We begin by describing the alphabet. We assume |Σ| can be infinite and we let Σ be equal to the union of the following sets of symbols:
1.
{vi| for all i = 1,…, |V|}. Hence, there exists one symbol representing each vertex in G.
2.
{ci,j,m|i = 1,…,t; j = 1,…,t; m = 1,…, |E|}. There exists an unique symbol for each 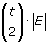strings produced for our reduction.
Hence, we have a total of number of symbols.
Next, we generate a set of strings S = {s1,1,1,…, s1,1,|E|, s1,2,1,…, s1,2,|E|,… ,st–1,t,|E|}. Every string has length t and will encode one edge of the input graph. There will be corresponding for each edge, however, encode the edges in different positions. For string si,j,m we encode edge em = (vr, vs), where 1 ≤ r < s ≤ |V|, but letting position i equal to vr and position j equal to vs and the remaining positions equal to ci,j,m. Hence, a string is given by
To clarify our reduction, we give an example. Let G = (V, E) be an undirected graph with V = v1, v2, v3, v4 and edges E = {(v1, v2), (v1, v3), (v1, v4), (v2, v3)} and let our CLIQUE instance have G and t = 3. Figure 1 illustrates the reduction. Using G, we exhibit the above construction of strings, which we denote as S. We claim that there exists a clique of size 3 if and only if there exists a string s* of length ℓ = t = 3 and subset S* of S of size 3 where d(s,si) ≤ d for all si∈S*. In this example the center string s is equal to v1v2v3 and each string in the set {v1v2c121, v1c132v3, c234v2v3} is such that each string in S* has Hamming distance at most 1 from s.
Figure 1
An illustration of the reduction fromCLIQUEto CSWO Example of the reduction from a CLIQUE instance G with t = 3 to an instance of CSWO with 12 strings with ℓ = t = 3, d = t – 2 = 1, and . In bold we have the set of strings S* = {s121, s132, s234} that corresponds to the clique containing the vertices {v1,v2,v3}. We note that S* is the only set such that |S*| = 3, which have Hamming distance at most d from s*.
Correctness of the Reduction
The following two lemmas establish the correctness of the reduction.
Lemma 1 For a graph with a t-clique, the construction in Subsection produces a CSWO instance with a set S∗ and a string s of length such that for every si∈ S* d(si, s) ≤ d.
Proof Let the input graph have a clique of size t. Let vα1, vα2, …, vαt be the vertices in the clique C of size t and without loss of generality, assume α1< α2<…< αt . Then we claim that the there exists a subset of vertices that have distance at most t – 2 from the string s = vα1vα2 …vαt. Consider the first edge of the clique (vα1, vα2) of the clique then it follows that the string s11r = vα1vα2 [c11r ]t–2, where edge r has endpoints vα1vα2, is contained in the set of strings {s111, s112,…, s11|E|}. Clearly, H(s11r,s) = t – 2. For each edge in C we have we have a string in S that has distance at most t – 2 from s and our lemma follows from this construction.
For the reverse direction, we need to prove that the existence a subset S* of and a string s where d(s, si) ≤ t – 2 for all si∈S* implies the existence of a clique in G with t vertices.
Lemma 2The t symbols of the center string correspond to the t vertices of clique in the input graph
Proof. Let S* be the subset of S of size such that s has distance t – 2 from each string in S*. Since ℓ = t, n* = t, d = t – 2 and for each symbol ci,j,m there exists only a single string i = 1, …,t, j = 1, …,t and m = 1,…, |E| it follows from the Pigeonhole principle that the center string s only contains symbols from {vi| for all i = 1,…,|V|}. Without loss of generality assume s is equal to vα1vα2 …vαt for αv1, αv2,…,αvt∈ {1,…, |V|}. Consider any pair αi, αj for 1 ≤ i < j ≤ t and consider the set of strings Si,j = {si,j,1, si,j,2,…, si,j,|E|}. Recall that Si,j contains a string corresponding to each edge e = (r, s) in E which has vr at the i th position and vs at the jth position and ci,j,m at all remaining positions. Therefore, we can only find a string in Si,j that has distance at most t – 2 from s if vαí is at the i th position and vαj is at the j th position; and such a string exists if and only if there is an edge in G connecting vαí to vαj. Hence, the center string s implies there exists an edge between any pair of vertices in G in the set {vα1vα2 … vαt} and by definition the vertices form a clique.
Our main theorem follows directly from Lemma 1 and Lemma 2. We note that the hardness for the combination of all three parameters also implies the hardness for each subset of the three.
Theorem 1 CSWO with unbounded alphabet is W[1]-hard with respect to the parameters ℓ, d, and n*.
Since there exists a trivial reduction from the CLOSEST STRING problem to CSWO (i.e. simply set k = 0 in CSWO), there cannot exist a fixed parameter tractable algorithm for CSWO with k as a parameter, unless P = NP; such an algorithm would contradict the NP-hardness of CLOSEST STRING.
Fact 1 CSWO is W[1]-hard with respect to the parameter k and when |Σ| ≤ 2, unless P = NP.
Conclusions
We introduced the CSWO problem, and proved with unbounded alphabet size and parameterized by ℓ, d and n* it is W[1]-hard. We also gave fixed parameter algorithms for the problem when parameterized by d and k, and with unbounded alphabet size. In the case of a fixed alphabet size, we showed CSWO is fixed parameter tractable when parameterized by n = n* + k. Table 1 summarizes these tractability and intractability results.
Currently, the fixed parameter tractability of the CSWO problem when parameterized by d, n* and Σ, and by n* and k, remains open (see Table 1). In addition, the existence of efficient, non-trivial approximation algorithms for this problem warrants further investigation.
Table 1
Parameterized tractability of CSWO
Parameter(s)
|Σ| is a parameter
|Σ| is unbounded
ℓ, d, n*
FPT (trivial)
W[1]-hard (*)
ℓ
FPT (trivial)
W[1]-hard (*)
d, n*
Open
W[1]-hard (*)
d, k
FPT (*)
FPT (*)
n*, k
FPT
Open
k
W[1]-hard (trivial)
W[1]-hard (trivial)
An overview of the fixed parameter tractability and intractability of the CSWO. Asterisk denotes the new results found in this paper.
Declarations
Acknowledgement
CB is supported by NSERC Grant OGP0046506, NSERC Grant OGP0048487, Canada Research Chair program, MITACS, and Premier’s Discovery Award. BM is supported by NSERC (RGPIN 238748-2006), China 863 National High-tech R&D Program (2008AA02Z313), and a startup grant at University of Waterloo. We are also grateful to the referees for their many helpful comments.
This article has been published as part of BMC Bioinformatics Volume 12 Supplement 1, 2011: Selected articles from the Ninth Asia Pacific Bioinformatics Conference (APBC 2011). The full contents of the supplement are available online at http://www.biomedcentral.com/1471-2105/12?issue=S1.
Authors’ Affiliations
(1)
David R. Cheriton School of Computer Science, University of Waterloo
References
Dopazo J, Rodríguez A, Sáiz J, Sobrino F: Design of primers for PCR amplification of highly variable genomes. Computer Applications in the Biosciences 1993, 9: 123–125.PubMedGoogle Scholar
Lanctot J, Li M, Ma B, Wang S, Zhang L: Distinguishing string selection problems. Information and Computation 2003, 41–55. 10.1016/S0890-5401(03)00057-9Google Scholar
Lucas K, Busch M, Össinger S: Thompson J: An improved microcomputer program for finding gene-and gene family-specific oligonucleotides suitable as primers for polymerase chain reactions or as probes. Computer Applications in the Biosciences 1991, 7: 525–529.PubMedGoogle Scholar
Proutski V, Holme E: Primer master: A new program for the design and analyiss of PCR primers. Computer Applications in the Biosciences 1996, 12: 253–255.PubMedGoogle Scholar
Deng X, Li G, Li Z, Ma B, Wang L: Genetic design of drugs without side-effects. SIAM Journal on Computing 2003, 32(4):1073–1090. 10.1137/S0097539701397825View ArticleGoogle Scholar
Tompa M, Li N, Bailey TL, Church GM, De Moor B, Eskin E, Favorov AV, Frith MC, Fu Y, Kent WJ, et al.: Assessing computational tools for the discovery of transcription factor binding sites. Nature Biotechnology 2005, 23: 137–144. 10.1038/nbt1053View ArticlePubMedGoogle Scholar
Ben-Dor A, Lancia G, Perone J, Ravi R: Banishing bias from consensus strings. Proc. of 8th CPM 1997, 247–261.Google Scholar
Pavesi G, Mauri G, Pesole G: An algorithm for finding signals of unknown length in DNA sequences. Bioinformatics 2001, 17: S207-S214.View ArticlePubMedGoogle Scholar
Pevzner P, Sze S: Combinatorial approaches to finding subtle signals in DNA strings. Proc. of 8th ISMB 2000, 269–278.Google Scholar
Frances M, Litman A: On covering problems of codes. Theoretical Computer Science 1997, 30(2):113–119.Google Scholar
Fellows M, Gramm J, Neidermeier R: On the Parameterized Intractability of Closest Substring and Related Problems. Proc. of 19th STACS 2002, 262–273.Google Scholar
Fellows M, Gramm J, Niedermeier R: On The Parameterized Intractability Of Motif Search Problems. Combinatorica 2006, 26: 141–167. 10.1007/s00493-006-0011-4View ArticleGoogle Scholar
Gramm J, Niedermeier R, Rossmanith P: Fixed-parameter algorithms for closest string and related problems. Algorithmica 2003, 37: 25–42. 10.1007/s00453-003-1028-3View ArticleGoogle Scholar
Li M, Ma B, Wang L: Finding similar regions in many strings. Journal of Computer and System Sciences 2002, 65: 73–96. 10.1006/jcss.2002.1823View ArticleGoogle Scholar
Ma B: A polynomial time approximation scheme for the closest substring problem. Proc. of 11th CPM 2000, 99–107.Google Scholar
Ma B, Sun X: More efficient algorithms for closest string and substring problems. Proc. of 12th ACM RECOMB 2008, 396–409.Google Scholar
Garey M, Johnson D: Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman; 1979.Google Scholar
Lenstra W: Integer programming with a fixed number of variables. Mathematics of Operations Research 1983, 8: 538–548. 10.1287/moor.8.4.538View ArticleGoogle Scholar
Chen ZZ, Ma B, Wang L: A Three-String Approach to the Closest String problem. Proc. of 16th COCOON (to appear) 2010.Google Scholar
Wang L, Zhu B: Efficient algorithms for the closest string and distinguishing string selection problems. Proc. of 3rd FAW 2009, 261--270.Google Scholar
Zhao R, Zhang N: A more efficient closest string algorithm. Prof. of 2nd BICoB (to appear) 2010.Google Scholar
Marx D: Closest Substring Problems with Small Distances. SIAM Journal on Computing 2008, 38: 1382–1410. 10.1137/060673898View ArticleGoogle Scholar
Gramm J, Guo J, Niedermeier R: On Exact and Approximation Algorithms for Distinguishing Substring Selection. Proc. of 14th FCT 2003, 261–272.Google Scholar
This article is published under license to BioMed Central Ltd. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
) ≤ d where
is a length ℓ substring of s
i
. Fellows et al. [11] showed that CLOSEST SUBSTRING is W[1]-hard with respect to the number of input strings n even for a binary alphabet. When Σ is unbounded the problem is W[1]-hard with respect to the parameters ℓ, d and n[11]. Most recently, Marx [23] proved the problem is W[1]-hard with combined parameters n and d even if the alphabet is binary, which resolved an open problem stated in [11, 12, 24].
strings such that G has a clique of size t if and only if there is a subset of S of size
, denoted as S*, where there exists a string x such that d(s
i
,x) ≤ d for all s
i
∈ S*. We let ℓ = t and d = t – 2. We assume that t > 2 since t ≤ 1 produces trivial cases.
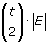strings produced for our reduction.
number of symbols.
strings S = {s1,1,1,…, s1,1,|
E
|, s1,2,1,…, s1,2,|
E
|,… ,s
t–
1,
t
,|
E
|}. Every string has length t and will encode one edge of the input graph. There will be
corresponding for each edge, however, encode the edges in different positions. For string s
i
,
j
,
m
we encode edge e
m
= (v
r
, v
s
), where 1 ≤ r < s ≤ |V|, but letting position i equal to v
r
and position j equal to v
s
and the remaining positions equal to c
i
,
j
,
m
. Hence, a string is given by
strings, which we denote as S. We claim that there exists a clique of size 3 if and only if there exists a string s* of length ℓ = t = 3 and subset S* of S of size 3 where d(s,s
i
) ≤ d for all s
i
∈ S*. In this example the center string s is equal to v1v2v3 and each string in the set {v1v2c121, v1c132v3, c234v2v3} is such that each string in S* has Hamming distance at most 1 from s.
strings, which we denote as S. We claim that there exists a clique of size 3 if and only if there exists a string s* of length ℓ = t = 3 and subset S* of S of size 3 where d(s,s
i
) ≤ d for all s
i
∈ S*. In this example the center string s is equal to v1v2v3 and each string in the set {v1v2c121, v1c132v3, c234v2v3} is such that each string in S* has Hamming distance at most 1 from s.
. In bold we have the set of strings S* = {s121, s132, s234} that corresponds to the clique containing the vertices {v1,v2,v3}. We note that S* is the only set such that |S*| = 3, which have Hamming distance at most d from s*.
vertices that have distance at most t – 2 from the string s = v
α
1v
α
2 …v
αt
. Consider the first edge of the clique (v
α
1, v
α
2) of the clique then it follows that the string s11
r
= v
α
1v
α
2 [c11
r
]
t–
2, where edge r has endpoints v
α
1v
α
2, is contained in the set of strings {s111, s112,…, s11|
E
|}. Clearly, H(s11
r
,s) = t – 2. For each edge in C we have we have a string in S that has distance at most t – 2 from s and our lemma follows from this construction.
and a string s where d(s, s
i
) ≤ t – 2 for all s
i
∈ S* implies the existence of a clique in G with t vertices.
such that s has distance t – 2 from each string in S*. Since ℓ = t, n* = t, d = t – 2 and for each symbol c
i
,
j
,
m
there exists only a single string i = 1, …,t, j = 1, …,t and m = 1,…, |E| it follows from the Pigeonhole principle that the center string s only contains symbols from {v
i
| for all i = 1,…,|V|}. Without loss of generality assume s is equal to v
α
1v
α
2 …v
αt
for α
v
1, α
v
2,…,α
vt
∈ {1,…, |V|}. Consider any pair α
i
, α
j
for 1 ≤ i < j ≤ t and consider the set of strings S
i
,
j
= {s
i
,
j
,1, s
i
,
j
,2,…, s
i
,
j
,|
E
|}. Recall that S
i
,
j
contains a string corresponding to each edge e = (r, s) in E which has v
r
at the i th position and v
s
at the jth position and c
i
,
j
,
m
at all remaining positions. Therefore, we can only find a string in S
i
,
j
that has distance at most t – 2 from s if v
α
í
is at the i th position and v
αj
is at the j th position; and such a string exists if and only if there is an edge in G connecting v
αí
to v
αj
. Hence, the center string s implies there exists an edge between any pair of vertices in G in the set {v
α
1v
α
2 … v
αt
} and by definition the vertices form a clique.