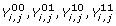- Proceedings
- Open access
- Published:
Efficient algorithms for reconstructing gene content by co-evolution
BMC Bioinformatics volume 12, Article number: S12 (2011)
Abstract
Background
In a previous study we demonstrated that co-evolutionary information can be utilized for improving the accuracy of ancestral gene content reconstruction. To this end, we defined a new computational problem, the Ancestral Co-Evolutionary (ACE) problem, and developed algorithms for solving it.
Results
In the current paper we generalize our previous study in various ways. First, we describe new efficient computational approaches for solving the ACE problem. The new approaches are based on reductions to classical methods such as linear programming relaxation, quadratic programming, and min-cut. Second, we report new computational hardness results related to the ACE, including practical cases where it can be solved in polynomial time.
Third, we generalize the ACE problem and demonstrate how our approach can be used for inferring parts of the genomes of non-ancestral organisms. To this end, we describe a heuristic for finding the portion of the genome ('dominant set’) that can be used to reconstruct the rest of the genome with the lowest error rate. This heuristic utilizes both evolutionary information and co-evolutionary information.
We implemented these algorithms on a large input of the ACE problem (95 unicellular organisms, 4,873 protein families, and 10, 576 of co-evolutionary relations), demonstrating that some of these algorithms can outperform the algorithm used in our previous study. In addition, we show that based on our approach a ’dominant set’ cab be used reconstruct a major fraction of a genome (up to 79%) with relatively low error-rate (e.g. 0.11). We find that the ’dominant set’ tends to include metabolic and regulatory genes, with high evolutionary rate, and low protein abundance and number of protein-protein interactions.
Conclusions
The ACE problem can be efficiently extended for inferring the genomes of organisms that exist today. In addition, it may be solved in polynomial time in many practical cases. Metabolic and regulatory genes were found to be the most important groups of genes necessary for reconstructing gene content of an organism based on other related genomes.
Introduction
Reconstruction of ancestral genomic sequences is a classical problem in molecular evolution. The first algorithm for reconstructing ancestral genomic sequences was suggested around 40 years ago by Fitch [1]. This algorithm was based on the Maximum Parsimony (MP) criteria and was designed for sequences with a binary alphabet. A few years later the algorithm was generalized by Sankoff, for inputs with non-binary alphabets and multiple edge weights [2]. More recently, similar approaches for optimizing the maximum likelihood score (ML; instead of maximum parsimony) emerged [3–8].
Reconstruction of ancestral genomic sequences was employed in many biological and bioinformatical studies in recent years. Specifically, it was used for studying various evolutionary questions [9–18]), for aligning genomic sequences [19], and for inferring ancestral SNPs [20].
In practice, the solution space of the ancestral sequences reconstructing problem, tends to be populated with a large number of local and global maxima, obscuring algorithm accuracy. Thus, the ancestral sequences inferred by the conventional approaches tend to have a relatively large number of errors. Based on the fact that functionally and physically interacting proteins tend to co-evolve [21–25], we have recently suggested the Ancestral Co-Evolver approach, for improving the accuracy of reconstructed ancestral genomes [26, 27]. Our approach was based on utilizing information embedded in the co-evolution of functionally/physically interacting proteins.
The current study includes novel algorithms for the ACE problem. In addition, we generalize our previous approach showing that co-evolution is not only an important statistical force that can be employed to infer ancestral sequences, but it can also be used for inferring the genomes of organisms existing today (i.e. the leaves of the evolutionary tree). Such an approach can be utilized for the analysis of metagenomic data (see, for example, [28]). Furthermore a generalization of this approach can be used for inferring biological networks (e.g. protein-protein interactions and metabolic networks [29, 30]). As we demonstrate in this paper, this approach is also a useful tool for studying genomic and molecular evolutionary.
The rest of the paper is organized as follows. In subsection ’Definitions and Preliminaries’, we define the notations and computational problems studied in the paper. In subsection ’Some Computational Issues’, we deal with the computational hardness of the ACE problem. We show that in many practical cases it can be solved in polynomial time. In subsection ’Methods and Algorithms’, we describe the biological data used in this study, and a new set of algorithms for solving the ACE problem. In addition, we describe a new approach for detecting a part of the genome, which can then be used for inferring the remaining gene content, with the lowest error rate. In the last three subsections, we demonstrate the ACE algorithms’ performance, by analyzing a large dataset (an evolutionary tree, genomes and co-evolutionary relations) corresponding to 95 unicellular organisms [26], and discuss their features. The section ’Conclusions’ includes concluding remarks and a discussion.
Results and discussion
Definitions and preliminaries
For simplicity, we assume a binary alphabet. However, all the results here can be easily generalized to models with more than two characters (see examples in [26]). Each genome is represented by a binary sequence corresponding to the states of all the proteins in the genome. If the value of the i-th bit of the sequence is ’1’, it means that the i-th protein is encoded in the genome; if the i-th bit of the sequence is ’0’, then the i-th protein is not encoded in the genome. As we explain later, there may also be bits with unknown values (i.e. it is not known if the protein appears in the genome or not); we use the label ’?’ for such cases. In the current study, our aim is to in addition infer these missing values.
In this work, neighbor sites in the input sequences evolve independently, when they do not have a known co-evolutionary relation. Thus, the basic components in the model and algorithms are single characters. Our goal is to reconstruct the ancestral states and missing states at the leaves, for a set of organisms  of size
of size  . A phylogenetic tree is a rooted binary tree T = (V(T), E(T)) with a leaf labeling function λ, where V(T) is the set of vertices and E(T) the set of edges.
. A phylogenetic tree is a rooted binary tree T = (V(T), E(T)) with a leaf labeling function λ, where V(T) is the set of vertices and E(T) the set of edges.
In our context, a weight table is attributed to each edge (u, v) = e ∈ E(T). This weight table includes a weight (a positive real number), for each pair of labels of two vertices (u, v) = e.
In this work, we assume that each node in a phylogenetic tree corresponds to a different organism. The leaves in a phylogenetic tree correspond to organisms existing today  , while the internal nodes correspond to organisms that have become extinct
, while the internal nodes correspond to organisms that have become extinct  . Thus, we can name each node after its corresponding organism. Let O
T
(⋅) denote a function that returns the index of the organisms corresponding to each node in T, i.e. for every v ∈ V(T), O
T
(v) is the index of the organism (from
. Thus, we can name each node after its corresponding organism. Let O
T
(⋅) denote a function that returns the index of the organisms corresponding to each node in T, i.e. for every v ∈ V(T), O
T
(v) is the index of the organism (from  ) corresponding to v.
) corresponding to v.
The leaf labeling function is a bijection between the leaf set L(T) and the set of genomic sequences (or subsequences) corresponding to the organisms that exist today,  . In our binary case, each label is a binary sequence with missing entries and all the sequences have the same length. As with conventional ML/MP, we assume an i.i.d. case, where different characters in a sequence evolve independently, thus we can describe an algorithm for sequences of length one (i.e. each sequence is ′1′, ′0′, or ′?′).
. In our binary case, each label is a binary sequence with missing entries and all the sequences have the same length. As with conventional ML/MP, we assume an i.i.d. case, where different characters in a sequence evolve independently, thus we can describe an algorithm for sequences of length one (i.e. each sequence is ′1′, ′0′, or ′?′).
A full labeling of a phylogeny  , is a labeling of all the nodes of the tree such that the labels of the leaves that are not missing are the same as the non-missing values of λ, i.e., for all cases that are not missing values,
, is a labeling of all the nodes of the tree such that the labels of the leaves that are not missing are the same as the non-missing values of λ, i.e., for all cases that are not missing values,  . In the current study, we solve the gene content inference problem; where each character in a label corresponds to a protein in a genome. As previously stated, if the value of a character is ′1′ it means that the protein is coded in the genome and if it is ′0′ it means that the protein is not coded in the genome.
. In the current study, we solve the gene content inference problem; where each character in a label corresponds to a protein in a genome. As previously stated, if the value of a character is ′1′ it means that the protein is coded in the genome and if it is ′0′ it means that the protein is not coded in the genome.
A co-evolving forest F =(S F = {T1, T2, …}, E c (S F )) is a set of phylogenetic trees, S F , with identical topology that correspond to the same organisms [i.e. each tree has the same O(·)], and an additional set of edges, E c (S F ), that connect pairs of nodes in different trees. This set of edges represents the co-evolutionary relations between pairs of protein families. Edges in E c (S F ) must connect pairs of nodes that correspond to the same organism (i. e. (v, u) ∈ E c (S F ), v ∈ V(T1), u ∈ V(T2) ⇒ OT1(v) = OT2(u); Figure 1); we call such pairs of nodes legal co-evolutionary pairs.
The Ancestral Co-Evolution A. A simple example of a co-evolving forest with three trees (each tree corresponds to a different gene family), and one co-evolution edge connecting node x2 in tree T1 and node y2 in tree T2; the weight table corresponding to this co-evolution edge is in red. The weight table corresponding to the tree edge (x1, x2) in T1 is in green. The values at the leaf x5 in tree T1 and the leaf y5 in tree T2 are missing. B. The co-evolutionary graph corresponding to the co-evolving forest in A.
The edges in E c (S F ) are named co-evolution edges, while edges that constitute the evolutionary trees are named tree edges. For example, Figure 1A. includes a co-evolving forest with two trees (the co-evolution edges are dashed with arrows, while the tree edges are continuous). In this work we assume that new co-evolutionary edges do not appear/disappear during evolution. Namely, we assume that if there is a co-evolutionary edge between a legal co-evolutionary pair of nodes in two trees, then all the legal co-evolutionary pairs of nodes in the two trees are connected by co-evolutionary edges. In this study, we also assume that there is no change in the co-evolutionary weight table, across legal co-evolutionary pairs of nodes corresponding to a pair of phylogenetic trees. However, with suitable biological support/data, the co-evolutionary weight tables may differ across a pair of evolutionary trees (reflecting changes in co-evolutionary relations across evolution). Thus, the parsimony score in the case of the ACE problem can capture the evolutionary events of proteins, while considering our belief regarding the dependencies between pairs of proteins.
A full labeling of a co-evolving forest is a full labeling,
is a full labeling,  , of all the nodes of the phylogenetic trees in S
F
, including the missing values at their leaves. The roots of a co-evolving forest are the set of roots of the phylogenetic trees in the co-evolving forest.
, of all the nodes of the phylogenetic trees in S
F
, including the missing values at their leaves. The roots of a co-evolving forest are the set of roots of the phylogenetic trees in the co-evolving forest.
As mentioned, a co-evolving forest also includes a weight table for each co-evolution edge and each tree edge. These weight tables are cost functions, which return a real positive number for each pair of labels at the two ends of the edge. In the case of tree edges, these weights reflect the probability of a mutation along the edge. In the case of co-evolution edges, these weights reflect the distribution of mutual occurrence of the labels of the nodes at the ends of the edge.
This leads us to the formal definition of the problem we are concerned with, the Ancestral Co-Evolution (ACE) problem with missing variables at the leaves, which is a generalization of the problem defined in [27]:
Problem 1 Ancestral Co-Evolution (ACE)
Input: A co-evolving forest, F = (S F , E c (S F )) (possibly with missing labels at the leaves), and a real number, B.
Question: Are there labels for the internal nodes of all the trees in the co-evolving forest, and the missing values at the leaves, such that the sum of the corresponding weights along all the tree edges and the co-evolution edges is less than B?
Note that in general, it is not necessarily required that the solution for each tree separately, will be the most parsimonious. The minimal sum of edge weights corresponding to a co-evolving forest, F (Problem 1) is denoted the cost of F. A co-evolutionary graph is an undirected graph, which describes the co-evolution edges in the co-evolving forest. In such a graph, each node corresponds to a tree in the co-evolving forest, and two nodes are connected by an edge, if there is at least one co-evolution edge between their corresponding trees. A connected component in the co-evolving forest is a sub-set of trees, such that their corresponding nodes in the co-evolutionary graph induce a connected component (see an example in Figure 1B.).
It is easy to see (more details in [26]) that if the optimization criterion is maximum likelihood (see, for example, [4]) for i.i.d models such as Jukes Cantor (JC) [31], Neyman [32], or the model of Yang et al.[33], the problem can be formalized as a maximum parsimony problem with a non-binary alphabet and multiple edge weights [2]. Thus, the Ancestral co-evolution problem without co-evolution edges (|E c (S F )| = 0), can describe a Maximum Likelihood (ML) problem.
In this paper, we also study the problem of finding a sub-set of the genes in a genome (one of the leaves in some of the phylogenetic trees), such that it can be used for reconstructing the rest of the gene content of this genome with minimal error-rate, based on the information embedded in the co-evolutionary forest (see Figure 2). We named this problem the Dominant Co-Evolutionary Set (DCES) problem (more details in section ’Algorithm for the Dominant co-evolutionary set problem’).
The Dominant Co-Evolutionary Set (DCES) problem A. The input to the DCES problem is a phylogenetic forest and a target genome (red) corresponding to a certain leaf in all the phylogenetic trees (the leftmost leaf in this example). The goal is to find a subset of proteins in the target genome such that given this subset of proteins (and the phylogenetic forest), it will be possible to infer the rest of the genome; in this example, proteins from gene families T1, T2, T3, T4, T6, T8 are used to infer the rest of the target genome (the proteins marked with ′?′; proteins T5, T7, T9 in the example). B. The problem can be reduced to a version of the dominant set problem [34] (see details in section ’Algorithm for the Dominant co-evolutionary set problem’). In the reduction we build a graph that includes a node for each gene family and pairs of gene families are connected with edges if they have a strong co-evolutionary relation; we want to find a dominant set in this graph.
Some computational issues
It has been shown that the ACE problem is NP-hard by a reduction from the MAX-2SAT problem [27]. In this section, we describe another simple reduction from/to the ACE problem, and will use it to prove that the hardness of the problem is related to anti-correlative weight tables. In many practical cases the anti-correlative relations are rare; thus, the ACE problem can be solved in polynomial time.
Let (a, b, c, d) denote the notation for a weight table (either a weight table of tree edges or of co-evolutionary edges, see Figure 1), where the costs a, b, c, d are for the labels 00, 01, 10, 11 respectively at the ends of the edge. Assume that the analyzed co-evolutionary forest includes two types of edges: 1) green (”good”) edges of the form (0,1,1, 0) corresponding to a positive correlation between the two proteins along the tree edges (i.e. the two proteins tend to appear/disappear in the same organism); 2) red (”bad”) edges of the form (1, 0, 0, 1), corresponding to a negative correlation between the two proteins (i.e. when one of the proteins appears in a genome, the second usually does not). Note that these two types of edges are the most informative ones (e.g. in terms of entropy). Indeed, such edge weights have been included in previous studies. For example, the classical algorithm of Fitch [1] considers only green edges.
If all the edges are green, the problem becomes a Min-Cut (defined below), which is polynomially solvable. Thus, if all the weight tables are of the form (0, 1, 1, 0) (as in [1]), any topology of the co-evolutionary forest of the ACE problem, can be solved in polynomial time.
Problem 2 Min-weighted Cut
Input: A weighted graph G = (V, E, W(E)).
Solution: A cut C = (S, T) which is a partition of V of the graph G.
Objective: Minimize the total weight of all edges that are in the set {(u, v) ∈ E|u ∈ S, v ∈ T}.
In the following lemma we formally show a reduction from the ACE problem to the min-cut problem, for the case where all the weight tables are of the form (0, 1, 1, 0). A similar reduction can be employed for reducing min-cut to ACE.
Lemma 1 The ACE problem with only weight tables of the form (0, 1, 1, 0) can be reduced to the min-cut problem.
Proof Given a phylogenetic forest as an input to the ACE, problem the instance of the min-cut problem includes a graph G = (V, E), that is reconstructed as follows: V is the set of nodes of the phylogenetic forest (i.e. the nodes of all the phylogenetic trees); E is the set of edges in the co-evolutionary forest (both tree edges and co-evolutionary edges).
Now, we will show that there is a cut of size |C| in G iff the score of the ACE problem is |C|.
⇒ Suppose that there is a minimal cut C = (S, T), such that the size of the cut is |C|. In the ACE problem, label all the nodes in S with ’1’, and all the nodes in T with ’0’. The edges (tree edges or co-evolutionary edges), which increase the score of the ACE problem include only the edges of the cut (other edges have two identical labels at their ends). By the definition of the weight table, each of these edges increases the ACE score by 1. Thus, there exists a labeling for the ACE problem with score |C|.
⇐ Suppose that there is a labeling for the ACE problem with score |C|. In the min-cut problem select all the nodes that have the label ’1’ to be in S, and all the nodes with label ’0’ to be in T. By the definition of the weight tables, only edges with non-identical labels at their ends contribute 1 to the ACE score, and each of these edges is in the cut. Thus, the size of the cut is |C|.
□
However, if all tables are of the form (1, 0, 0, 1), the problem becomes Min-UnCut, which is NP-hard (like Max-Cut) [34].
Problem 3 Min-weighted UnCut
Input: A weighted graph G = (V, E, W(E)).
Solution: A cut C = (S, T) which is a partition of V of a graph G.
Objective: Minimize the total weight of all edges that are not in the cut (i.e. minimize the set {(u, v) ∈ E|((u, v) ∈ S) ∨ ((v, u) ∈ T)}.
In the following lemma we formally show a reduction from the ACE problem, to the min-Uncut problem, for the case that all the weight tables are of the form (1, 0, 0, 1). A similar reduction can be applied for reducing min-Uncut to ACE.
Lemma 1 The ACE problem with all the weight tables of the form (1, 0, 0, 1) can be reduce to the min-UnCut problem.
Proof Given a phylogenetic forest as an input to the ACE problem, the instance of the min-Uncut problem includes a graph, G = (V, E) that is reconstructed as follows: V is the set of nodes of the phylogenetic forest (the nodes of all the phylogenetic trees); E is the set of edges in the co-evolutionary forest (tree edges and co-evolutionary edges).
⇒ Suppose that there is a minimal UnCut C = (S, T) such that the size of the UnCut is |C|. In the ACE problem label all the nodes in S with ’1’, and all the nodes in T with ’0’. The edges (tree edges or co-evolutionary edges) that increase the score of the ACE problem, are only the edges that are not in the cut (other edges do not have two identical labels at their ends and according to the weight table the weight of such edges is 0). By the definition of the weight table, each of these edges increases the ACE score by 1. Thus, there is a labeling for the ACE problem with score |C|.
⇐ Suppose that there is a labeling for the ACE problem with score |C|. In the min-UnCut problem, select all the nodes that have the label ’1’ to be in S, and all the nodes with label ’0’ to be in T. By the definition of the weight tables, only edges with two identical labels at their ends contribute 1 to the ACE score, and each of these edges are is not in the cut. Thus, the size of the UnCut is |C|.
□
Let tu denote the upper bound on the number of possible assignments to the internal nodes, and the missing values at the leaves of a single tree, in the co-evolutionary forest S F (i.e. in a co-evolutionary forest in which the evolutionary trees have n nodes tu = 2n). Let T MinCut (S F ) denote the (polynomial) computational time it takes to solve the min-cut problem corresponding to the co-evolutionary forest S F . It is easy to see that if the co-evolutionary forest includes r red edges, the optimal assignment can be found in O(tu2·r · T MinCut (S F )) = O(22·r·n · T MinCut (S F )), by implementing the min-cut algorithm on all possible assignments to the evolutionary trees at the ends of the red edges. Thus, this is a Fixed-Parameter Tractable (FPT) algorithm with a running time that is exponential with the number of red edges and the size of the evolutionary trees. For example, if we consider only the co-evolutionary information (see, for example, [26]), an input with r red edges can be solved in O(2r · T MinCut (S F )) time complexity.
Finally, it is easy to see that the results reported in this section can be generalized to the case where the edge tables include α instead of 1 and β instead of 0, and β is small relatively to α (i.e. β <α/|E(S F )|; and E(S F ) is the set of edges in the phylogenetic forest).
Algorithms
This section includes a few algorithmic approaches for inferring genomic sequences by co-evolution. The first approach was suggested in our previous paper, whilst the rest are novel.
A FPT algorithm and approximation heuristics
Here we describe very briefly the FPT algorithm and corresponding approximation heuristics that were described in [27]. This heuristic approach has 3 major steps: 1) clustering/dividing the co-evolutionary forest to small enough sub-forests (with relatively many co-evolutionary relations among phylogenetic trees from the same cluster/sub-forests); 2) Using a dynamic programming algorithm (a version of the Sankoff algorithm [2]) for finding exact solutions for each of these sub-forests; 3) Improving the solution found in step 2) greedily. The algorithm that is employed in step 2) finds the exact optimal solution for the ACE problem, but its running time is exponential with the size of the largest connected component in the co-evolutionary graph.
A Quadratic and Linear Programming
In this subsection we demonstrate how the ACE problem can be formulated as a Quadratic Programming (QP), and a Linear Programming (LP) problem. To this end we define several variables that will be used in these formulations. For each node v
i
in the co-evolutionary forest (i.e. one of the nodes in the phylogenetic trees that are in the phylogenetic forest), we define a variable y
i
; In addition, for each edge (v
i
, v
j
) in the co-evolutionary forest, we define four variables, which we name edge variables, one for each possible assignment of the ends of the edge  . Let
. Let  denote the four weights in the weight table of the edge (v
i
, v
j
) (see Figure 3). We will start with a definition of Quadratic Programming (QP). Let x ∈ R
n
denote a set of n variables; let c, x
L
, x
U
∈ R
n
denote vectors of real numbers; let A ∈ R
m
∗
n
be a matrix of real numbers; F is a symmetric positive-definite matrix; let b
L
, b
u
∈ R
m
be vectors of m real numbers. The general formulation of a Quadratic Programming is as follows:
denote the four weights in the weight table of the edge (v
i
, v
j
) (see Figure 3). We will start with a definition of Quadratic Programming (QP). Let x ∈ R
n
denote a set of n variables; let c, x
L
, x
U
∈ R
n
denote vectors of real numbers; let A ∈ R
m
∗
n
be a matrix of real numbers; F is a symmetric positive-definite matrix; let b
L
, b
u
∈ R
m
be vectors of m real numbers. The general formulation of a Quadratic Programming is as follows:
min x f(x) = 0.5 · xt · F · x + ct · x
such that:
-
(1)
x L ≤ x ≤ x U
-
(2)
b L ≤ Ax ≤ b U
In the case of Integer Quadratic Programming (IQP) or integer programming, all the variables are integers (i.e. either ’0’or ’1’).
The ACE problem can be easily defined as an IQP problem (see Figure 3). In this case we consider the y
i
variables defined above. These variables are 0 ≤ y
i
≤ 1 in the case of QP and y
i
= {0, 1} in the case of IQP. Based on these variables and the weights in the weight tables, we define for each edge (v
i
, v
j
) four terms:  (details in Figure 3; in the case of y
i
= {0, 1} only one of these terms is larger than zero). The (Quadratic) optimization function is
(details in Figure 3; in the case of y
i
= {0, 1} only one of these terms is larger than zero). The (Quadratic) optimization function is  . In the case of y
i
= {0, 1}, for each edge only one of the terms in the weight tables is larger than zero.
. In the case of y
i
= {0, 1}, for each edge only one of the terms in the weight tables is larger than zero.
As we show in the next section, solving IQP for large inputs of the ACE is time consuming, and not practical for large inputs. However, for small inputs, such an approach may be useful.
In the rest, of this subsection we will show how to formulate a Linear Programming (LP) relaxation or an Integer Programming (IP) of the ACE problem. The general formulation of a linear programming is as follows:
min x f(x) = ct · x
such that:
-
(1)
x L ≤ x ≤ x U
-
(2)
b L ≤ Ax ≤ b U
The following is the reduction to a LP relaxation of the ACE problem (Figure 3):
A. The variables:
-
(1)
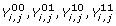
are edge variables, such that each of them hold a value stating whether this corresponding assignment (i.e. the labeling of the two ends of the edge) was chosen for this edge, (in the integer programming case for each i, j only one of the terms is 1 and the rest are 0).
-
(2)
The y i variables. Each of them should hold the value stating the appropriate assignment for node i in the co-evolutionary forest (0 or 1 in the case of integer programming).
B. The target function:
x is a vector that includes all the variables mentioned in A. The costs that are related to the edge variable (i, j) are the corresponding weights in the weight table (Figure 3); i.e. . The cost corresponding to all the variables y
i
is 0.
. The cost corresponding to all the variables y
i
is 0.
C. Constraints on the variables:
(1) All variables must receive a value from [0, 1], i.e.:

0 ≤ y i ≤ 1
(2) Every edge must get exactly one assignment, i.e.:

(3) Every node must have a consistent assignment across all edges touching it. Thus, for every edge (i, j) touching node i, it must hold that  . Thus, in the integer case either y
i
= 0 or y
i
= 1. If y
i
= 0 every edge that includes i gets an assignment where node i is assigned with 0; similarly, for y
i
= 1 the edges that include are assigned such that node i is equal to 1.
. Thus, in the integer case either y
i
= 0 or y
i
= 1. If y
i
= 0 every edge that includes i gets an assignment where node i is assigned with 0; similarly, for y
i
= 1 the edges that include are assigned such that node i is equal to 1.
D. The Size of the problem:
Let E(S F ) and V(S F ) denote the total number of edges and nodes in the co-evolutionary forest respectively. The number of variables in the LP: 4 · |E(S F )| + |V(S F )|; The number of constraints in the LP: 3 · |E(S F )|.
Thus, with the reductions described in this subsection, packages that solve IQP, QP, LP, or IP can be used for solving the ACE problem.
A Min-Cut based heuristic
As we mentioned in section ’Some Computational Issues’, when the input includes only green edges it becomes a Min-Cut and can be solved in polynomial time.
Thus, a possible heuristics based on this phenomenon includes the following steps:
-
1)
Consider only the ”good” edges (round the weight table of these edges to be of the type (0, A, A, 0)) and find the mean cut solution for these edges. We implemented the min-cut algorithm of Stoer-Wagner [35].
-
2)
Start with the min-cut solution found in 1) and run a greedy algorithm based on the entire set of edges (see [27] ).
If the number of ”bad” edges is small one can implement an FPT that is exponential with the number of ”bad” edges ( for each assignment of the bad edges, run max-cut to find the assignment for the ”good” edges; as was mentioned in section ’Some Computational Issues’).
Algorithm for the Dominant co-evolutionary set problem
In this subsection we describe a heuristic for solving the Dominant Co-Evolutionary Set (DCES) problem. The aim is to find a set of gene families (for example, COGs [36]), that we name a ’dominant set’ (DS), such that in a certain organism (i.e. a target genome) the proteins corresponding to this DS can be used for reconstructing the rest of the proteins in the genome, with an error-rate lower than a certain threshold. The missing proteins in the genome are reconstructed based on the DS, co-evolution and evolutionary information.
The central idea of our heuristic is a reduction of the DCES problem to a version of the dominant set problem which is described below. The following is the formal definition of the dominant set problem.
Problem 4 Dominant set
Input: A graph G = (V, E, W(E)).
Solution: A subset D ∈ V such that every vertex not in D is joined to at least one member of D by some edge.
Objective: Minimize the size of D.
Let W1 and W2 denote two thresholds. A gene family is a specific phylogenetic tree in the co-evolutionary forest. The relevant values corresponding to such a gene family in the current context are the labels at the leaves of the gene family tree. Given an input co-evolutionary forest and a target genome j, we perform the following steps (see also figure 4):
-
1.
Set a variable F i for each gene family in the co-evolutionary forest, and generate a graph with a node for each F i . For each F i there is a related binary vector corresponding to the values of the gene family in the different organisms. F i (j) = 1 designates that the gene family is encoded in genome j, F i (j) = 0 designates that the gene family is not encoded in genome j.
-
2.
Set a variable T i for each protein in the target genome (e.g. genome j). This variable represents how well we can infer the value of F i (j) based on the tree structure, and the labels of the other leaves of the tree (i.e. the values of the gene family F i in the rest of the organisms).
-
3.
Let MP(Ti|F i (j) = 0), MP(Ti|F i (j) = 1) denote the parsimony score of the evolutionary tree corresponding to the gene family F i , when setting the values of this gene family in genome j (the target genome) to be F i (j) = 0 and F i (j) = 1 respectively. Connect each T i as a node to the corresponding F i node with an edge weight W(Ti) = |MP(Ti|F i (j) = 0) – MP(Ti|F i (j) = 1)|/(min{MP(Ti|F i (j) = 1), MP(Ti|F i (j) = 0)}). Roughly speaking a larger W(Ti) signifies that with higher probability we can reconstruct F i (j) based on the evolutionary tree of F i .
-
4.
Based on the binary vector related to each F i , compute for each F i its empirical entropy, H(F i ); compute for each pairs of variables F i , F l the empirical mutual information (I(F i , F l )). Connect each pair of variables F i , F l by an edge with weight I(F i , F l ).
-
5.
The result of the previous steps is a weighted graph that represents the relations between all the F i and T i variables defined above (see figure 4). We want to find a minimal set (DS) of F i variables such that each variable, F i not in the DS, either has a strong connection to its T i variable (i.e. its inference strength, based on the evolutionary tree as the edge weight to the T i variable, is above W2) or/and it has strong connections to the other nodes in the DS (i.e. it can be inferred based on the co-evolutionary information – there is a set of nodes F k 1 , F kn , in the DS such that [H(F i ) – (∑ kj ∈ DS I(F i , F kj ))] <W1).
-
6.
All the nodes F i that have weak co-evolutionary relations H(F i ) – (∑ kj I(F i , F kj ) >W1 and their connection to the tree (T i ) is weak <W2 should be in the resultant DS.
-
7.
A DS with the thresholds W1 and W2, is a DS such that for each node F i outside the DS either a. H(F i ) – (∑ kj : kj ∈ DS I(F i , F ki ) <W1 or b. W(T i ) >W2
We used the following greedy algorithm to find the minimal dominant set with the thresholds W1 and W2:
A. Start with all the nodes as a DS.
B. At each stage, remove a node F
j
such that  is minimal.
is minimal.
C. Stop if  .
.
-
8.
Given the DS, the missing values in the target genome (i.e. unknown F k (j)) were reconstructed in the following manner:
A. Start with an initial guess of the missing values (e.g. the one suggested by the DS and/or the T i variables).
B. Based on this initial guess, infer all the labels of the co-evolutionary forest (with one of the algorithms for the ACE problem previously mentioned).
C. Change the labels of the missing values to improve the general parsimony score, given the labels at the ancestral states.
D. Repeat stages B. and C. till convergence (the change in the ACE score is lower than a certain threshold).
Note that we use the following approximation: H(F
i
|F
k
1, F
k
2,..) ≈ H(F
i
) – I(F
i
, F
k
1) – I(F
i
, F
k
2) – … Thus, it may be possible improve the accuracy (albeit increasing the running time) of the algorithm, by removing from the DS in each step the node F
k
, that minimizes  . In addition, if one requires a range of sizes for dominant sets (and error rates) the thresholds W1, W2 may be altered.
. In addition, if one requires a range of sizes for dominant sets (and error rates) the thresholds W1, W2 may be altered.
Comparison of the different algorithms
In this section, we briefly report a comparison of the run times, and the quality of the solutions found by the aforementioned algorithms. The linear, integer, and quadratic programming were implemented in Matlab, using the commercial programming of TOMLAB optimization environment (http://tomopt.com/tomlab/). We used a Xeon 2.6GHz 64bit 2 cores x 4 cpu’s, with 4GB of memory. As can be seen (see Table 1), the linear programming archived a result that is optimal in terms of the quality of the solution (lowest and optimal parsimony score). The solution was similar to the one obtained by the ACE [27] (98.9 % of the inferred sites were identical). In addition, the running time of the FPT heuristic for solving the ACE [27] was shorter than all other algorithms, and the quality of the solutions found by this approach (with and without the greedy stage) is similar (though lightly higher) to the one obtained by the linear programming approach. The integer programming achieved the optimal solution (as the linear programming), but with a long run time. The integer quadratic programming and the min-cut heuristic, though theoretically interesting, were not practical for the large input we analyzed. The IQP failed due to memory problems, and the min-cut heuristic was not near convergence after a week of running.
The results of the linear programming
As mention in the previous section, the linear programming generally returns a solution ∈ [0, 1]. Thus, in general, the result found by the LP is a lower bound on the optimal (minimal) possible solution of the ACE problem. Interestingly, when we implemented the (linear programming) relaxation that was defined in the previous section, on the biological input, the values of all the variables that were assigned by the linear programming were ∈ {0, 1}. Thus, the linear programming found an optimal (and legal) solution for the problem. This result demonstrates, in accordance with subsection ’Some Computational Issues’, that in many practical cases the optimal solution can be found in polynomial time (for example by linear programming). In addition, this result shows that the ACE solutions found by the FPT heuristic in [26], are very near optimal (only 0.060550424/0.06 = 0.92% higher).
Demonstration of the algorithm for the dominant co-evolutionary set problem
We used the procedure for solving the DCES problem to analyze the genomes of six unicellular organisms. The first three bacteria were chosen according to their distance from the closest leaf in the phylogenetic tree: P. aeruginosa, D. radiodurans, and E. coliOHE. Among these three organisms, E. coliOHE has the closest leaf in the phylogenetic tree (other E. coli strains; 0.65% of the gene content is not similar) while P. aeruginosa has the lowest gene content similarity to its closest leaf in the phylogenetic tree (24% of the gene content is not similar). D. radiodurans has 18.3% non-similarity in gene content to its closest leaf in the phylogenetic tree. We analyzed three additional organisms: S. cereυisiae (an eukaryote; 2% dissimilarity to the closets leaf), A. pernix (an archaeon; 7% dissimilarity to the closest leaf), and B. aphidicola (an endosymbiont; 32% dissimilarity to the closest leaf).
The genome of each of these organisms was represented as a binary sequence, with 4873 entries (an entry for each gene families). The aim was to reconstruct parts of the genomes/sequences (i.e. determine the values, ’0’ or ’1’, of parts of the sequences) based on its remainder and the phylogenetic forest.
We modified the thresholds W1, W2 to obtain various dominant set sizes, and computed the error rate when reconstructing the rest of the genome based on the DS. In addition, in each case, we computed the percentage of the reconstructed sites, that were inferred based on co-evolutionary information (i.e. not based on the T i variables; see the algorithm in the previous section). The results are depicted in Figures 5 – 7. The error-rate is represented as the percentage of the total number of reconstructed sites that we correctly inferred. The size of the DS is represented as the percentage of the sites (out of 4873), that were used to reconstruct the remaining sites.
Error-rate results of the DCES problem. Implementation of the procedure for the DCES problem on six genomes: E. coliOHE (A.), D. radiodurans (B.), and P. aeruginosa (C.), A. pernix (D.), B. aphidicola (E.) S. cerevisea (F.). For each organism, the graph includes the error rate (red; % of the sites not in the DS were not reconstructed accurately based on the DS) and the % of sites that were reconstructed based on co-evolutionary relations (blue; i.e. their value cannot be inferred based on their evolutionary tree), for different sizes of the dominant set (% from the total number of proteins in the genome, x-axis).
Running time results of the DCES problem. The figure includes the running time of 90 implementations of the DCES algorithm on the six analyzed organisms (15 samples for each organism), as a function of the size of the DS. The different sizes of the DS are a result of modifying the two thresholds (W1 and W2).
Error rate
As can be seen, large portions of the genomes of organisms, such as P. aeruginosa and D. radiodurans (66% and 79% of the genome respectively), which do not have an evolutionary close neighbor in the co-evolutionary forest, can be reconstructed based on the rest of the corresponding genome, with a relatively low error rate (0.2 and 0.11 respectively). In addition, our results demonstrate that co-evolutionary information (and not only phylogenetic information) was used for the reconstruction of these genomes (up to 20% of the sites were inferred based on co-evolutionary information). It seems that co-evolutionary information is more important when there are no evolutionary close organisms in the co-evolutionary forest; for example, in the case of E. coli and S. cerevisiae, the fraction of sites that was inferred based on co-evolutionary data was relatively low. B. aphidicola is interesting as it undergoes a (’rare’) process of adaptation to a symbiotic lifestyle, where the gene set of the ancestor has been selectively reduced, so as to retain only those genes and pathways required for the new lifestyle [37, 38]. The unique evolution of this endosymbiont challenged our approach, which is based on the statistic of the evolution of ’normal’ (non-endosymbiont) organisms. Indeed the error rate for this organism was slightly higher, but still surprisingly low (e.g. 0.1 for DS of size 35%).
Finally, the algorithm performed well for genomes from all three domains of life (error rate 0.04 and 0.005 for A. pernix and S. cerevisiae respectively).
Running times
Figure 6 includes the running time of the procedure for solving the DCES problem as a function of the size of the DS. It includes the running time of 90 implementations of the DCES algorithm on the six analyzed organisms (15 samples for each organism), as a function of the size of the DS. The different sizes of the DS are a result of modifying the two thresholds (W1 and W2).
The typical running time for the analyzed phylogenetic forest is around 25 minutes (the range is between 8 and 97 minutes). Thus, the approach has practical running times.
As can be seen in the figure, the running time usually increases with the size of the DS. The running time when the DS includes less than 100 gene families is around 19 minutes, whilst the running time for cases with a DS larger than 3500 gene families is around 32 minutes.
Biological analysis of the DS genes
We focused on S. cerevisiae aiming at understanding the properties of the DS genes. We decided to analyze S. cerevisiae as it is one of the most studied organisms in the analyzed dataset, with various public large scale measurements.
We began with studying the cellular function of the DS genes. To this end we performed functional enrichment analysis of the genes in the DS (Methods), based on the biological process ontology [39]. The results appear in Figure 7. As can be seen, the DS is mainly enriched with metabolic genes, genes related to transport, and genes related to various regulatory processes.
We continued with a study of the cellular characteristics of the DS genes. In each case we compared the genes in the DS to the relevant set of genes that are outside the DS (Methods). At the first stage, we checked if the dN/dS (non-synonymous substitution rate divided by synonymous substitution rate) of genes in the DS is significantly different than the dN/dS of other genes. To this end, we used the data of [40]. We found the dN/dS of genes in the DS is significantly higher (0.0566 vs. 0.052; KS-test, p = 1.3913 ∗ 10–5; Figure 8A). Next, we checked if the Protein Abundance (PA) of genes in the DS is significantly different than the PA of other genes. To this end, we used the data of [41]. We found the PA of genes in the DS is significantly lower (1.2 ∗ 104vs. 2.47 ∗ 104; KS-test, p = 4.083 ∗ 10–6; Figure 8B). Next, we checked if the number of PP-interactions (PPI) of genes in the DS is significantly different than the number of PPI of other genes. To this end, we used the data of [26]. We found the number of PPI of the genes in the DS is significantly lower than the number of PPI of genes outside the DS (10.1 vs. 19.2; KS-test, p = 9.98 ∗ 10–12; Figure 8C).
The results presented in this section suggest that the DS genes include many metabolic genes, they have relatively high dN/dS, low protein abundance and low number of protein-protein interactions.
Genes with a high dN/dS tend to change rapidly between organisms, thus can be inferred less well based on other existing genomes. In addition, genes with a relatively low number of protein-protein interactions and protein abundance also tend to appear in a DS. Such genes have less functional constraints and can thus evolve faster. Furthermore, as such genes have less physical interactions and thus less co-evolutionary relations with other genes, their state can not be inferred by most of the other genes, and they should be added to the DS. The fact that most of the genes in the DS are metabolic and regulatory genes, demonstrates that these are the processes that tend to change among the analyzed organisms, supporting previous studies in the field [24, 42–45].
Conclusions
In this study we describe a few computational approaches for inferring genomes based on co-evolutionary relations. The algorithms described in this study are based on reductions to commonly employed approaches, such as linear programming (LP), quadratic programming (QP), and min-cut. As there are many free and commercial packages that solve LP and QP, the reductions describe in this study should be very useful in practice.
Furthermore, the current study also includes new results related to the computational complexity of the ACE problem. We report cases where an exact solution to the ACE problem can be found in polynomial time. As we demonstrate in the main text, such cases are common when analyzing biological data. Thus, in practice many times the optimal solution of the ACE problem can be found in a relatively short time. In addition, we describe a linear programming relaxation that returns a solution that can be used as a lower bound on the possible minimal solution. Thus, it can be used for estimating the quality of a legal solution found by the algorithms mentioned in this paper.
It is important to emphasize that the problem of finding a minimal and maximal cut can be solved more efficiently in graphs with certain properties. Thus, the approach min/max-cut reduction, suggested in this study, may be useful in such cases. For example, it is known that the max-cut problem can be solved in polynomial time in planar graphs [46]. Thus, if the co-evolutionary forest is planer, the ACE with only red edges can also be solved in polynomial time.
Finally, we formally describe for the first time strategies for 1) inferring a genome based on a portion of it, and 2) finding a part (subset of the proteins) of a target genome such that it will be possible to reliably reconstruct the rest of the target genome base on this subset. Thus, by using this strategy one can sequence only a section of a genome of interest, and infer its entire gene content. This approach can be generalized to deal with the inference of cellular networks (e.g. metabolic networks and protein-protein interaction networks). In these cases, the input includes a target organism with a partial cellular network and the cellular networks in other organisms; the aim is to infer the rest of the cellular network of the target organism. One of the major differences in the case of this generalization, is the fact that both the nodes and the edges of the network need be inferred.
Methods
The analyzed co-evolutionary forest
The evolutionary tree, the labeling of the leaves, and the co-evolutionary information were downloaded from [26]. This data includes the gene content (4873 gene families) of 95 unicellular organisms (bacteria, archaea, and eukaryotes). The classification to gene families was based on the COG database [36, 47]. See [26] for more details regarding the input.
The co-evolutionary edges
We used the co-evolutionary data from [26]. These data include pairs of proteins that exhibit various physical and functional interactions. We ranked pairs of proteins (co-evolutionary edges) according to the empirical mutual information between their gene content vectors. For two proteins x, and y let p(x), p(y), be the empirical distribution of the state (’1’ or ’0’; appear or disappear in the genome) of the proteins over the analyzed organisms, and let p(x, y) be the joint empirical distribution of the protein pair. The corresponding empirical mutual information is I(x, y) = Σp(x, y) · log(p(x, y)/p(x) · p(y)). Higher mutual information corresponds to stronger co-evolution. The final co-evolutionary forest included 10, 576 edges (Figure 9). The weight table of a pair of COGs included the –log(·) of the joint empirical distribution of the two COG.
To estimate the number of red and green edges in the co-evolutionary forest we computed the KL distance between the weight table of each edge and the weight tables of the green and red edges that were defined in subsection ’Some Computational Issues’. The empirical KL distance is defined as KL(x||y) = Σp(x) · log(p(x)/p(y)). We found that 142 of the edges were red (KL distance to the red weight table is lower) and the rest of them were green (KL distance to the green weight table is lower).
The red edges relates to pairs of COG that tend to mutually exclude each other (if a gene of one of the COG appear in the organism the second usually does not appear in this organism). For example the edge between COG 1467 (Eukaryotic-type DNA primase, catalytic (small) subunit) and COG 2812 (predicted type IV restriction endonuclease) is red. The first one tend to appear in archaea eukaryotes and the second in bacteria.
GO enrichment analysis and analysis of the cellular features of DS genes
In all the GO enrichment analyzes, the set of S. cerevisiae genes that was mapped to the DS COGs was compared to the S. cerevisiae genes that have a mapping to COGs as a background. Similarly, the PA, PPI, and dN/dS of the set of S. cerevisiae genes that was mapped to the DS COGs was compared to the features of the S. cerevisiae genes that have mappings to COGs.
References
Fitch W: Toward defining the course of evolution: minimum change for a specified tree topology. Syst. Z 1971, 20: 406–416. 10.2307/2412116
Sankoff D: Minimal mutation trees of sequences. SIAM Journal on Applied Mathematics 1975, 28: 35–42. 10.1137/0128004
Barry D, Hartigan J: Statistical analysis of humanoid molecular evolution. Stat. Sci 1987, 2: 191–210. 10.1214/ss/1177013353
Pupko T, Peer I, Shamir R, Graur D: A Fast Algorithm for Joint Reconstruction of Ancestral Amino Acid Sequences. Mol. Biol. Evol 2000, 17(6):890896.
Elias I, Tuller T: Reconstruction of ancestral genomic sequences using likelihood. J Comput Biol 2007, 14(2):216–37. 10.1089/cmb.2006.0101
Felsenstein J: PHYLIP (phylogeny inference package) version 3.5c. Technical report, Department of Genetics, University of Washington, Seattle 1993.
Krishnan NM, Seligmann H, Stewart C, Koning APJ, Pollock DD: Ancestral Sequence Reconstruction in Primate Mitochondrial DNA: Compositional Bias and Effect on Functional Inference. MBE 2004, 21(10):1871–1883. 10.1093/molbev/msh198
Pagel M: The Maximum Likelihood Approach to Reconstructing Ancestral Character states of Discerete Characters on Phylogenies. Systematic Biology 1999, 48(3):612–622. 10.1080/106351599260184
Gaucher E, Thmoson J, Burgan MF, Benner SA: Inferring the palaeoenvironment of ancient bacteria on the basis of resurrected proteins. Nature 2003, 425: 285–288. 10.1038/nature01977
Hillis DM, Huelsenbeck JP, Cunningham CW: Application and accuracy of molecular phylogenies. Science 1994, 264: 671–677. 10.1126/science.8171318
Cai W, Pei J, Grishin NV: Reconstruction of ancestral protein sequences and its applications. BMC Evolutionary Biology 2004, 4: e33. 10.1186/1471-2148-4-33
Tuller T, Girshovich Y, Sella Y, Kreimer A, Freilich S, Kupiec M, Gophna U, Ruppin E: Association between translation efficiency and horizontal gene transfer within microbial communities. Nucleic Acids Res 2011.
Zhang J, Rosenberg HF: Complementary advantageous substitutions in the evolution of an antiviral RNase of higher primates. Proc. Natl. Acad. Sci. USA 2002, 99: 5486–5491. 10.1073/pnas.072626199
Thornton J, Need E, Crews D: Resurrecting the ancestral steroid receptor: ancient origin of estrogen signaling. Science 2003, 301: 1714–1717. 10.1126/science.1086185
Tauberberger J, Reid A, Lourens R, Wang R, Jin G, Fanning TG: Characterization of the 1918 influenza virus polymerase genes. Nature 2005, 437: 889–893. 10.1038/nature04230
Jermann T, Opitz J, Stackhouse J, Benner S: Reconstructing the evolutionary history of the artiodactyl ribonuclease superfamily. Nature 1995, 374: 57–59. 10.1038/374057a0
Ouzounis C, Kunin V, Darzentas N, Goldovsky L: A minimal estimate for the gene content of the last universal common ancestor–exobiology from a terrestrial perspective. Res. Microbiol 2006, 157: 57–68. 10.1016/j.resmic.2005.06.015
Blanchette M, Green ED, Miller W, Haussler D: Reconstructing large regions of an ancestral mammalian genome in silico. Genome Res 2004, 14: 2412–2423. 10.1101/gr.2800104
Hudek AK, Brown DG: Ancestral sequence alignment under optimal conditions. BMC Bioinformatics 2005.
Hacia J, Fan J, Ryder O, Jin L, Edgemon K, Ghandour G, Mayer R, Sun B, Hsie L, Robbins C, Brody L, Wang D, Lander E, Lipshutz R, Fodor S, Collins F: Determination of ancestral alleles for human single-nucleotide polymorphisms using high-density oligonucleotide arrays. Nat. Genet 1999, 22(2):164–7. 10.1038/9674
Juan D, Pazos F, Valencia A: High-confidence prediction of global interactomes based on genome-wide coevolutionary networks. Proc. Natl. Acad. Sci. U. S. A 2008, 105(3):934939.
Sato T, Yamanishi Y, Kanehisa M, Toh H: The inference of proteinprotein interactions by co-evolutionary analysis is improved by excluding the information about the phylogenetic relationships. Bioinformatics 2005, 21(17):3482–3489. 10.1093/bioinformatics/bti564
W J, et al.: Identification of functional links between genes using phylogenetic profiles. Bioinformatics 2003, 19: 1524–1530. 10.1093/bioinformatics/btg187
Tuller T, Kupiec M, Ruppin E: Co-evolutionary Networks of Genes and Cellular Processes Across Fungal Species. Genome Biol 2009, 10.
Felder Y, Tuller T: Discovering Local Patterns of Co-evolution. RECOMB-CG 2008, 55–71.
Tuller T, Birin H, Gophna U, Kupiec M, Ruppin E: Reconstructing Ancestral Gene Content by Co-Evolution. Genome Res 2010, 20: 122–32. 10.1101/gr.096115.109
Tuller T, Birin H, Kupiec M, Ruppin E: Reconstructing ancestral genomic sequences by co-evolution: formal definitions, computational issues, and biological examples. J. Comput. Biol 2010, 17(9):1327–44. 10.1089/cmb.2010.0112
Tringe S, Mering C, Kobayashi A, Salamov A, Chen K, Chang H, Podar M, Short J, Mathur E, Detter J, Bork P, Hugenholtz P, Rubin E: Comparative Metagenomics of Microbial Communities. Science 2005, 308(5721):554–557. 10.1126/science.1107851
Skrabanek L, Saini H, Bader G, Enright A: Computational prediction of protein-protein interactions. Mol Biotechnol 2008, 38: 1–17. 10.1007/s12033-007-0069-2
Forster J, Famili I, Fu P, Palsson B, Nielsen J: Genome-Scale Reconstruction of the Saccharomyces cerevisiae Metabolic Network. Genome Res 2003, 13: 244–253. 10.1101/gr.234503
Jukes T, Cantor CR: Evolution of protein molecules. In Mammalian protein metabolism. Edited by: H. N. Munro. Academic Press, New York; 1969:21–123.
Neyman J: Molecular studies of evolution: A source of novel statistical problems. In Statistical Decision Theory and Related Topics. Edited by: S. Gupta and Y. Jackel. Academic Press, New York; 1971:127.
Yang Z, Kumar S, Nei M: A new method of inference of ancestral nucleotide - and amino acid sequences. Genetics 1995, 141: 1641–1650.
Garey M, Johnson D: Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman; 1979.
Stoer M, Wagner F: A simple min-cut algorithm. J. ACM 1997, 44(4):585–591. 10.1145/263867.263872
T R, et al.: The COG database: an updated version includes eukaryotes. BMC Bioinformatics 2003., 4(41):
Dale C, Moran N: Molecular interactions between bacterial symbionts and their hosts. Cell 2006, 126: 453465.
Pe’rez-Brocal V, Gil R, Ramos S, Lamelas A, Postigo M, Michelena J, Silva F, Moya A, Latorre A: A Small Microbial Genome: The End of a Long Symbiotic Relationship? Science 2006, 314(5797):312–313. 10.1126/science.1130441
Eden E, Navon R, Steinfeld I, Lipson D, Yakhini Z: GOrilla: a tool for discovery and visualization of enriched GO terms in ranked gene lists. BMC Bioinformatics 2009, 10: 48. 10.1186/1471-2105-10-48
Wall D, Hirsh A, Fraser H, Kumm J, Giaever G, Eisen M, Feldman M: Functional genomic analysis of the rates of protein evolution. Proc. Natl. Acad. Sci. USA 2005, 102(15):5483–5488. 10.1073/pnas.0501761102
Ghaemmaghami S, Huh W, Bower K, Howson R, Belle A, Dephoure N, Weissman EOJ: Global analysis of protein expression in yeast. Nature 2003, 425(6959):737–741. 10.1038/nature02046
Zhang X, Kupiec M, Gophna U, Tuller T: Analysis of coevolving gene families using mutually exclusive orthologous modules. Genome Biol Evol 2011, 3: 413–23. 10.1093/gbe/evr030
Jovelin R, Phillips P: Evolutionary rates and centrality in the yeast gene regulatory network. Genome Biol 2009, 10(4):R35. 10.1186/gb-2009-10-4-r35
Fraser H, Hirsh A, Steinmetz L, S C, Feldman M: Evolutionary Rate in the Protein Interaction Network. Science 2002, 296(5568):750–752. 10.1126/science.1068696
Robichaux R, Purugganan M: Accelerated regulatory gene evolution in an adaptive radiation Marianne Barrier. Proc Natl Acad Sci U S A 2001, 98(18):1020810213.
Hadlock F: Finding a Maximum Cut of a Planar Graph in Polynomial Time. SIAM J. Comput 1975, 4(3):221225.
J L, et al.: STRING 8–a global view on proteins and their functional interactions in 630 organisms. Nucleic Acids Res 2009, 37: D412–6. 10.1093/nar/gkn760
Acknowledgements
We would like to thank Hadas Zur, Oded Schwartz, Elchanan Mossel, Eytan Ruppin, and Martin Kupiec for helpful discussions. T.T. was partially supported by a Koshland fellowship at the Weizmann Institute of Science and his travel was supported by EU grant PIRG04-GA-2008-239317.
This article has been published as part of BMC Bioinformatics Volume 12 Supplement 9, 2011: Proceedings of the Ninth Annual Research in Computational Molecular Biology (RECOMB) Satellite Workshop on Comparative Genomics. The full contents of the supplement are available online at http://www.biomedcentral.com/1471-2105/12?issue=S9.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
HB and TT participated in the design and execution of the study; HB and TT analyzed the results; TT participated in the preparation of this manuscript. HB and TT read and approved the final manuscript.
Hadas Birin and Tamir Tuller contributed equally to this work.
Rights and permissions
This article is published under license to BioMed Central Ltd. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Birin, H., Tuller, T. Efficient algorithms for reconstructing gene content by co-evolution. BMC Bioinformatics 12 (Suppl 9), S12 (2011). https://doi.org/10.1186/1471-2105-12-S9-S12
Published:
DOI: https://doi.org/10.1186/1471-2105-12-S9-S12