- Proceedings
- Open access
- Published:
Genome dedoubling by DCJ and reversal
BMC Bioinformatics volume 12, Article number: S20 (2011)
Abstract
Background
Segmental duplications in genomes have been studied for many years. Recently, several studies have highlighted a biological phenomenon called breakpoint-duplication that apparently associates a significant proportion of segmental duplications in Mammals, and the Drosophila species group, to breakpoints in rearrangement events.
Results
In this paper, we introduce and study a combinatorial problem, inspired from the breakpoint-duplication phenomenon, called the Genome Dedoubling Problem. It consists of finding a minimum length rearrangement scenario required to transform a genome with duplicated segments into a non-duplicated genome such that duplications are caused by rearrangement breakpoints. We show that the problem, in the Double-Cut-and-Join (DCJ) and the reversal rearrangement models, can be reduced to an APX-complete problem, and we provide algorithms for the Genome Dedoubling Problem with 2-approximable parts. We apply the methods for the reconstruction of a non-duplicated ancestor of Drosophila yakuba.
Conclusions
We present the Genome Dedoubling Problem, and describe two algorithms solving the problem in the DCJ model, and the reversal model. The usefulness of the problems and the methods are showed through an application to real Drosophila data.
Introduction
Gene duplication is an important source of variations in genomes. Recently, several studies have highlighted biological evidence for abundant segmental duplications that occur around breakpoints of rearrangement events in the evolution of eukaryotes.
In mammals, an evidence for a strong association between duplications, genomic instability and large-scale chromosomal rearrangements in primate evolution was first reported in [1]. Later in [2], a study of all evolutionary rearrangement breakpoints between human and mouse genomes reported that 53% of the breakpoints were associated with segmental duplications, as compared to 18% expected in a random assignment of breaks. In [3], a first study of the human-mouse rearrangement breakpoints, considering only synteny blocks of length larger than 100Kb and duplicated sequences of length larger than 10Kb, showed that 25% (122/461) of the breakpoints contained duplicated sequences of length greater than 10kb.
The association between segmental duplications and regions of breaks of synteny was also reported in the Drosophila species group. In [4], an analysis of the breakpoints of Drosophila yakuba compared to two related species, Drosophila simulans and Drosophila melanogaster, revealed that the breakpoint regions of 59% of the reversals (17/29) were associated with inverted duplications of genes or other nonrepetitive sequences. Further evidences of the recurrent presence of repetitive sequences near breakpoints of rearrangement in the evolution of Drosophila were also reported in [5–7].
A rearrangement event is an operation that modifies the organization of a given genome by cutting the genome at some points called breakpoints to glue the exposed extremities in a different way. The biological phenomenon called breakpoint-duplication results in the presence of the same genomic segment on both extremities of a breakpoint in a rearrangement. Several biological models have been presented to explain the presence of duplicated sequences at rearrangement breakpoint regions. These models are based on DNA breaks repairs that produce duplicated segments because of staggered Single-Strand-Breaks [3, 4], or non-reciprocal genetic exchange in Double-Strand-Breaks [5]. Most of these biological models support a nonrandom model of chromosomal evolution that implicates a predominance of recurrent small-scale duplications and large-scale evolutionary rearrangements within specific fragile regions. Moreover, the genetic instability of such regions is often suggested to be the cause rather than the consequence of duplicated genomic architecture [3, 8]. Interestingly, a growing number of the breakpoint-duplications detected in Supra-primates evolution have also been linked to recurrent chromosomal rearrangements associated with common diseases in the human population [1–3, 8, 9]. In [10], breakpoint-duplications were also identified in humam sex chromosomes, allowing to order rearrangement events in time, based on the degree of divergence of the breakpoint-duplicated sequences.
In this paper, we are interested in using the segmental duplications of a given present-day genome that has undergone breakpoint-duplication rearrangements, in order to reconstruct a non-duplicated ancestral genome. We formally define the breakpoint-duplication phenomenon, and introduce a combinatorial problem called the Genome Dedoublíng problem. Given a genome that has undergone breakpoint-duplication rearrangements, possibly with other rearrangements events, the problem asks to find an ancestral genome such that the number of rearrangement events needed to tranform the ancestor into the given genome is minimal. Note that the Genome Dedoubling problem asks to find a non-dupliated ancestor of a given duplicated genomes, as the Genome Halving problem introduced in [11] that consists of, given a genome that has undergone a whole-genome duplication followed by rearrangement events, finding the ancestral genome that was present right before the whole-genome duplication event. However, the two problems and their solutions are different as they aim at recovering different types of duplication events, breakpoint-duplications and whole-genome duplications. As the Genome Halving problem is motivated by the whole-genome duplication events in molecular evolution, the Genome Dedoubling problem is motivated by breakpoint-duplication events in molecular evolution. Both problems are useful for the comparison of genomes with duplicated segments.
In the following, we study the Genome Dedoubling problem under the Double-Cut-and-Join (DCJ) and the reversal rearrangement models. In Section Methods, we formally present breakpoint-duplication (BD) rearrangements and the Genome Dedoubling Problem. We show that the problem can always be regarded as a Dedoubling Problem on totally duplicated genomes. In Section Genome dedoubling by DCJ, we study the problem under the DCJ model, on multichromosomal then unichromosomal genomes. We prove the NP-completeness of the problems by reduction to an APX-complete problem, and provide algorithms with a linear time complexity, except for an APX-complete part that is 2-approximable. In Section Genome dedoubling by reversal, we study the problem under the reversal model on oriented genomes, making use of some results of the Hannenhalli-Pevzner (HP) theory [12] on sorting by reversal described in [13, 14]. We provide an algorithm with a quadratic time complexity, except for an APX-complete part that is 2-approximabe. In Section Application, an application for the reconstruction of a non-duplicated ancestor of Drosophila yakuba, using data from [4], is presented.
Methods
In this section we give the main definitions and notations of duplicated genomes and rearrangements. Next, we generalize the definitions of rearrangements in order to introduce a formal definition of breakpoint-duplication rearrangements, and the Genome Dedoubling Problem studied in the paper.
Duplicated genomes
A genome consists of linear or circular chromosomes that are composed of genomic markers. Markers are represented by signed integers such that the sign indicates the orientations of markers in chromosomes. By convention, – –x = x. A linear chromosome is represented by an ordered sequence of signed integers surrounded by the unsigned marker ○ at each end indicating the telomeres. A circular chromosome is represented by a circularly ordered sequence of signed integers. For example, (1 2 –3) (○ 4 –5 ○) is a genome composed of one circular and one linear chromosome.
Each genome contains at most two occurrences of each marker. Two copies of a same marker in a genome are called paralogs. If a marker x is present twice, one of the paralogs is represented by  . By convention,
. By convention,  . Here, such markers represent segments duplicated by a breakpoint-duplication rearrangement.
. Here, such markers represent segments duplicated by a breakpoint-duplication rearrangement.
Definition 1 A duplicated genome is a genome in which a subset of the markers are duplicated.
For example,  is a duplicated genome where markers 1, 2, and 5 are duplicated. A non-duplicated genome is a genome in which no marker is duplicated. A totally duplicated genome is a duplicated genome in which all markers are duplicated. For example,
is a duplicated genome where markers 1, 2, and 5 are duplicated. A non-duplicated genome is a genome in which no marker is duplicated. A totally duplicated genome is a duplicated genome in which all markers are duplicated. For example,  is a totally duplicated genome.
is a totally duplicated genome.
An adjacency in a genome is a pair of consecutive markers. Since a genome can be read in two directions, the adjacencies (x y) and (–y –x) are equivalent. For example, the genome  has seven adjacencies,
has seven adjacencies,  , and
, and  .
.
Definition 2 A dedoubled genome is a duplicated genome G such that for any duplicated marker x in G, either , or
, or is an adjacency of G.
is an adjacency of G.
For example,  is a dedoubled genome. The reduction of a dedoubled genome G, denoted by GR, is the genome obtained from G by replacing every pair
is a dedoubled genome. The reduction of a dedoubled genome G, denoted by GR, is the genome obtained from G by replacing every pair  , or
, or  by a single marker x. For example the reduction of
by a single marker x. For example the reduction of  is GR = (1 –2) (○ –3 4 –5 ○).
is GR = (1 –2) (○ –3 4 –5 ○).
Rearrangement
A rearrangement operation on a given genome cuts a set of adjacencies of the genome called breakpoints and forms new adjacencies with the exposed extremities, while altering no other adjacency. In this paper, we consider two types of rearrangement operation called double-cut-and-join (DCJ) and reversal. In the sequel, the breakpoints of a rearrangement operation are indicated in the genome by the symbol ▲, and the new adjacencies are indicated in the genome by dots.
A DCJ operation on a genome G cuts two different adjacencies in G and glues pairs of the four exposed extremities to form two new adjacencies. For example, the following DCJ cuts adjacencies (1 2) and  to produce
to produce  and (–5 2).
and (–5 2).

A reversal on a genome G is a DCJ operation that cuts two adjacencies (a b) and (c d) in a chromosome of G of the form (… a b … c d …) to form two new adjacencies adjacencies (a –c) and (–b d), thus reversing the orientation of the segment of G beginning with marker b and ending with marker c. For example, the following reversal cuts adjacencies  and
and  and reverses the segment
and reverses the segment  .
.

A DCJ (resp. reversal) scenario between two genomes A and B is a sequence of DCJ (resp. reversal) operations allowing to transform A into B. The length of a scenario is the number of rearrangement operations composing the scenario.
The DCJ (resp. reversal) distance between two genomes A and B is the minimum length of a DCJ (resp. reversal) scenario between A and B.
Breakpoint-duplication rearrangements
We now generalize the definitions of rearrangement operations to account for possible duplications at their breakpoints.
A 1-breakpoint-duplication DCJ (1-BD-DCJ) operation on a genome G is a rearrangement operation that alters two different adjacencies (a b) and (c d) of G, by:
-
first adding marker
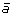 at the appropriate position to produce segment
at the appropriate position to produce segment 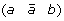 ,
, -
then applying a DCJ operation that cuts adjacencies
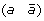 and (c d) to produce either (a d) and
and (c d) to produce either (a d) and 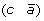 , or (a –c) and
, or (a –c) and  .
.
A 2-breakpoint-duplication DCJ (2-BD-DCJ) operation on a genome G is a rearrangement operation that alters two different adjacencies (a b) and (c d) of G, by:
-
first adding markers
 and
and 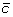 at the appropriate positions to produce segments
at the appropriate positions to produce segments 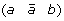 and
and 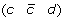 ,
, -
then applying a DCJ operation that cuts adjacencies
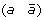 and
and 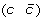 to produce either
to produce either 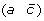 and
and 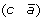 , or (a –c) and
, or (a –c) and 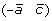 .
.
Definition 3 A breakpoint-duplication DCJ (BD-DCJ) operation on a genome G is either a 1-BD-DCJ operation, or a 2-BD-DCJ operation.
In the sequel, if some markers are duplicated by a BD-DCJ operation, they are indicated in bold font in the initial genome. For example, the following rearrangement is a 2-BD-DCJ operation that acts on adjacencies (–2 –1) and (4 –3), and duplicates markers 2 and 4. The intermediate step resulting in the duplication of markers 2 and 4 is shown above the arrow.

To summarize, a BD-DCJ operation consists of a first step in which one or two markers are duplicated, followed by a second step where a DCJ operation is applied. Similarly, we now define a breakpoint-duplication reversal (BD-reversal) operation.
Definition 4 A breakpoint-duplication reversal (BD-reversal) operation on a genome G is a BD-DCJ operation such that the DCJ operation applied in the second step of the BD-DCJ operation is a reversal.
For example, the following rearrangement is a BD-reversal that is a 1-BD-DCJ operation that acts on adjacencies (2 –1) and (–3 4), and duplicates marker 2.

A BD-DCJ scenario (resp. BD-reversal scenario) between a non-duplicated genome A and a duplicated genome B is a sequence composed of BD-DCJ (resp. BD-reversal) operations and possibly DCJ (resp. reversal) operations allowing to transform A into B.
Definition 5 Given a non-duplicated genome A and a duplicated genome B, the BD-DCJ distance (resp. BD-reversal distance) between A and B is the minimal length of a BD-DCJ (resp. BD-reversal) scenario between A and B.
We now give an obvious, but useful property allowing to reduce a BD-DCJ scenario to a DCJ scenario.
Proposition 1 Given a non-duplicated genome A and a duplicated genome B, for any a BD-DCJ (resp. BD-reversal) scenario between A and B, there exists a DCJ (resp. reversal) scenario of same length between a dedoubled genome D and B such that the reduction of D is A (DR = A).
Proof. Let S be a BD-DCJ (resp. BD-reversal) scenario between A and B. D is the genome obtained from A, by adding, for any marker x duplicated by a BD-DCJ operation in S, the marker  in a way to produce either adjacency
in a way to produce either adjacency  , or
, or  as done in S. Thus, DR = A. The DCJ (resp. reversal) scenario between DR and B having the same length as S, is the sequence of DCJ (resp. reversal) contained in S or in BD-DCJ (resp. BD-reversal) operations of S, with the same order as in S. ■
as done in S. Thus, DR = A. The DCJ (resp. reversal) scenario between DR and B having the same length as S, is the sequence of DCJ (resp. reversal) contained in S or in BD-DCJ (resp. BD-reversal) operations of S, with the same order as in S. ■
For example, in the following, a BD-reversal scenario of length 4 between A = (○ 1 2 3 4 5 ○) and  induces a reversal scenario of length 4 between
induces a reversal scenario of length 4 between  and B.
and B.

Genome dedoubling problem
We now state the genome dedoubling problems considered in this paper.
Genome dedoubling problem: Given a duplicated genome G, the DCJ (resp. reversal) genome dedoubling problem consists of finding a non-duplicated genome H such that the BD-DCJ (resp. BD-reversal) distance between H and G is minimal.
Given a duplicated genome G, we denote by d dcj (G) (resp. d rev (G)), the minimum BD-DCJ (resp. BD-reversal) distance between any non-duplicated genome and G. From Proposition 1, the following proposition is straightforward.
Proposition 2 Given a duplicated genome G, the DCJ (resp. reversal) genome dedoubling problem on G is equivalent to finding a dedoubled genome D such that the DCJ (resp. reversal) distance between D and G is minimal.
The next proposition describes a further reduction of the genome dedoubling problem on a duplicated genome G.
Proposition 3 Given a duplicated genome G, the DCJ (resp. reversal) genome dedoubling problem on G is equivalent to the DCJ (resp. reversal) genome dedoubling problem on the totally duplicated genome GT obtained from G by replacing every maximal subsequence of non-duplicated markers beginning with a marker x by the pair .
.
Proof. See proof in Additional file 1 (Supplemental proofs). ■
For example, solving the DCJ (resp. reversal) genome dedoubling problem on  is equivalent to solving it on
is equivalent to solving it on  . The transformations applied on G to obtain GT are indicated in bold font.
. The transformations applied on G to obtain GT are indicated in bold font.
In the sequel, G will always denote a totally duplicated genome, and we focus in Sections Genome dedoubling by DCJ and Genome dedoubling by reversal on the problem of finding a dedoubled genome D such that the DCJ (resp. reversal) distance between D and G is minimal.
Results
In this section, we first study the Genome Dedoubling Problem under the DCJ model. Next, we study the problem under the reversal model on oriented genomes described in the Hannenhalli-Pevzner (HP) theory on sorting by reversal [12–14].
Genome dedoubling by DCJ
In this section, G denotes a totally duplicated genome. In order to give a formula for the DCJ dedoubling distance of G, d dcj (G), we use a graph called the dedoubled adjacency graph of G.
Dedoubled adjacency graph
Definition 6 The dedoubled adjacency graph of G, denoted by , is the graph whose vertices are the adjacencies of G, and for any marker x there is one edge between the vertices (x u) and
, is the graph whose vertices are the adjacencies of G, and for any marker x there is one edge between the vertices (x u) and , and one edge between the vertices (y x) and
, and one edge between the vertices (y x) and .
.
An example of dedoubled adjacency graph is depicted in Fig. 1. In the following, we will simply refer to dedoubled adjacency graphs as adjacency graphs.
Note that all vertices in  have degree one or two. Thus, the connected components of
have degree one or two. Thus, the connected components of  are only paths and cycles. These paths and cycles are called elements of
are only paths and cycles. These paths and cycles are called elements of  .
.
Given a couple of paralogous markers  , an element of the graph
, an element of the graph  is said to contain the couple
is said to contain the couple  if it contains the edge linking vertices (x u) and
if it contains the edge linking vertices (x u) and  , or the edge linking vertices (y x) and
, or the edge linking vertices (y x) and  . By definition, a couple
. By definition, a couple  can possibly be contained in only one element A of
can possibly be contained in only one element A of  if element A contains both edges
if element A contains both edges  and
and  . In this case, A is said to contain twice the couple
. In this case, A is said to contain twice the couple  , and A is called a duplicated element of
, and A is called a duplicated element of  . If an element A contains no couple
. If an element A contains no couple  twice, then it is called a non-duplicated element of
twice, then it is called a non-duplicated element of  . If the two edges
. If the two edges  and
and  belong to two different elements A and B of
belong to two different elements A and B of  , then A and B will both contain
, then A and B will both contain  . In this case, we say that A and B intersect. If two elements A and B do not intersect, then we say that A and B are independent. For example in Fig. 1 the two paths of the adjacency graph are duplicated, while the three cycles are non-duplicated. The leftmost path and the leftmost cycle intersect because they both contain the couple
. In this case, we say that A and B intersect. If two elements A and B do not intersect, then we say that A and B are independent. For example in Fig. 1 the two paths of the adjacency graph are duplicated, while the three cycles are non-duplicated. The leftmost path and the leftmost cycle intersect because they both contain the couple  , while the two paths are independent. Given an element A of
, while the two paths are independent. Given an element A of  , the set induced by A is the set of couples
, the set induced by A is the set of couples  contained in A.
contained in A.
General sorting
In this section, we prove the following theorem:
Theorem 1 Let n be the number of couples of paralogous markers in G. Let C
i
be the maximum size of a subset of non-duplicated pairwise independent cycles in . The DCJ dedoubling distance of G is d
dcj
(G) = n – C
i
.
. The DCJ dedoubling distance of G is d
dcj
(G) = n – C
i
.
For example, in Fig. 1, the maximum size of a subset of non-duplicated pairwise independent cycles is 2 as there are three cycles, and the two rightmost cycles intersect. The distance would then be d dcj (G) = 8 – 2 = 6. To prove Theorem 1, we use the following properties:
Property 1 Let n be the number of couples of paralogous markers in G.
1. The maximum size C
i
of a set of non-duplicated pairwise independent cycles in the graph
 is n.
is n.
2. If G is dedoubled genome, then contains n non-duplicated pairwise independent cycles, each containing a single couple of paralogous markers, plus possibly other cycles. In this case, C
i
= n.
contains n non-duplicated pairwise independent cycles, each containing a single couple of paralogous markers, plus possibly other cycles. In this case, C
i
= n.
3. A DCJ operation can only alter the maximum size C i of a set of non-duplicated pairwise independent cycles by –1, 0 or +1.
Proof. See proof in Additional file 1 (Supplemental proofs). ■
Algorithm 1 is an algorithm that provides a n – C i length DCJ scenario transforming G into a dedoubled genome.

We now have all the pre-requisites to give the proof of Theorem 1. The proof can be found in Additional file 1 (Supplemental proofs).
Lemma 1 Choosing a maximum size set of non-duplicated pairwise independent cycles in is an APX-complete problem, approximable with an approximation ratio of 2.
is an APX-complete problem, approximable with an approximation ratio of 2.
Proof. See proof in Additional file 1 (Supplemental proofs). ■
From Lemma 1, the complexity of the Genome Dedoubling problem by DCJ follows immediately.
Corollary 1 The Genome Dedoubling problem by DCJ is NP-complete. Algorithm 1 solves the problem in linear time complexity, except for the computation of the set of cycles S i that is 2-approximable.
Sorting between linear unichromosomal genomes
In this section, we search for a minimum length DCJ scenario that transforms a duplicated genome consisting of a single linear chromosome into a dedoubled genome consisting of a single linear chromosome. The results of this section will then be used in the next section for the study of the Genome Dedoubling problem under the reversal model.
In this section and the sequel, G denotes a totally duplicated genome consisting of a single linear chromosome. In this case, the graph  contains exactly one path, and possibly several cycles.
contains exactly one path, and possibly several cycles.
Definition 7 The path in is said to be valid if it contains every couple
is said to be valid if it contains every couple of paralogous markers in G.
of paralogous markers in G.
A DCJ operation that merges a cycle c of  in the path p is a DCJ operation that acts on an adjacency of c and an adjacency of p, thus gathering c and p into a longer path.
in the path p is a DCJ operation that acts on an adjacency of c and an adjacency of p, thus gathering c and p into a longer path.
Note that if G is a dedoubled genome, then the path in  is necessarily valid. We call such a genome a dedoubled linear genome. So, if the path in
is necessarily valid. We call such a genome a dedoubled linear genome. So, if the path in  is not valid, then any DCJ scenario transforming G into a dedoubled linear genome will merge, in the path, cycles containing the couples
is not valid, then any DCJ scenario transforming G into a dedoubled linear genome will merge, in the path, cycles containing the couples  that are not contained in the path.
that are not contained in the path.
In the following, we always denote by m the minimum number of cycles required to make the path of  valid. We also denote by C
i
the maximum size of a subset of non-duplicated pairwise independent cycles. First, we have the following property:
valid. We also denote by C
i
the maximum size of a subset of non-duplicated pairwise independent cycles. First, we have the following property:
Property 2 Let C be the number of cycles in . We have C
i
= C – m.
. We have C
i
= C – m.
Proof. See proof in Additional file 1 (Supplemental proofs). ■
From Property 2, we then have the following lemma.
Lemma 2 Let n be the number of couples of paralogous markers in G. Let C be the number of cycles in . The minimum length d of a DCJ scenario transforming G into a dedoubled genome consisting of a single linear chromosome equals d = n – C + 2m.
. The minimum length d of a DCJ scenario transforming G into a dedoubled genome consisting of a single linear chromosome equals d = n – C + 2m.
Proof. See proof in Additional file 1 (Supplemental proofs). ■
From Property 2 and Lemma 2, we immediately have the following complexity.
Corollary 2 The problem of finding a DCJ scenario transforming G into a dedoubled genome consisting of a single linear chromosome is NP-complete. Algorithm 1, in which we add the line (2’: Merge in the path all the cycles that are not in S i ) between lines 2 and 3, solves the problem in linear time complexity, except for the computation of the set of cycles S i that is 2-approximable.
Genome dedoubling by reversal
We build and use a graph that behaves like the arc overlap graph used in [13] for the Hannenhalli-Pevzner theory of sorting by reversal [12]. The genome G consists of a single linear chromosome.
Dedoubled overlap graph
For any couple  of paralogous markers in G, the segment of
of paralogous markers in G, the segment of  is the smallest segment of G containing both markers x and
is the smallest segment of G containing both markers x and  . For example, in genome
. For example, in genome  , the segment of
, the segment of  is
is  , and the segment of
, and the segment of  is
is  .
.
Definition 8 The dedoubled overlap graph of G, denoted by , is the graph whose vertices are all the couples
, is the graph whose vertices are all the couples of paralogous markers of G, and there is an edge between two vertices
of paralogous markers of G, and there is an edge between two vertices and
and if the segments of u and v overlap.
if the segments of u and v overlap.
An example of dedoubled overlap graph is depicted in Fig. 4.a. In the following, we will simply refer to dedoubled overlap graphs as overlap graphs.
The vertex  of the graph
of the graph  is oriented if x and
is oriented if x and  have different signs in G, otherwise it is unoriented. If the vertex
have different signs in G, otherwise it is unoriented. If the vertex  is oriented then there exists a reversal operation denoted by
is oriented then there exists a reversal operation denoted by  that produces the adjacency
that produces the adjacency  and a reversal operation denoted by
and a reversal operation denoted by  that produces the adjacency
that produces the adjacency  . For example, in genome
. For example, in genome  is an oriented vertex of
is an oriented vertex of  .
.

The overlap graph of G behaves like arc overlap graphs used in [13] for the Hannenhali-Pevzner theory of sorting by reversal [12]. Indeed, given an oriented vertex  of the graph
of the graph  , performing the reversal
, performing the reversal  or
or  complements the subgraph induced by
complements the subgraph induced by  and all its neighbouring vertices, and changes the orientation of all vertices in this subgraph (see Fig. 4.b).
and all its neighbouring vertices, and changes the orientation of all vertices in this subgraph (see Fig. 4.b).
A connected component of the graph  is oriented if it contains at least one oriented vertex, otherwise it is unoriented. A genome is oriented if all connected components of the graph
is oriented if it contains at least one oriented vertex, otherwise it is unoriented. A genome is oriented if all connected components of the graph  are oriented, otherwise it is unoriented.
are oriented, otherwise it is unoriented.
Given an oriented vertex  of the graph
of the graph  , the score of
, the score of  is the number of oriented vertices in the overlap graph of the genome obtained after applying
is the number of oriented vertices in the overlap graph of the genome obtained after applying  on G. Note that the same number of oriented vertices is obtained after applying
on G. Note that the same number of oriented vertices is obtained after applying  on G.
on G.
Property 3
Let
 be an oriented vertex of
be an oriented vertex of
 of maximum score. Performing
of maximum score. Performing
 or
or
 does not create new unoriented connected components in the overlap graph of the genome obtained.
does not create new unoriented connected components in the overlap graph of the genome obtained.
Proof. See proof in Additional file 1 (Supplemental proofs). ■
In the sequel, we focus on sorting oriented genomes using reversal dedoubling scenarios. A totally duplicated genome G consisting of a single linear chromosome is called a valid-path genome if the single path in  is valid. Otherwise, it is called a non-valid-path genome.
is valid. Otherwise, it is called a non-valid-path genome.
Sorting an oriented valid-path genome
In this section, we consider an oriented valid-path genome G. With n being the number of couples of paralogous markers in G, we have the following theorem:
Theorem 2 Let G be an oriented valid-path genome. Let C be the number of cycles in . The reversal dedouhling distance of G is d
rev
(G) = n – C.
. The reversal dedouhling distance of G is d
rev
(G) = n – C.
Proof. See proof in Additional file 1 (Supplemental proofs). ■

Sorting an oriented non-valid-path genome
In this section, G denotes an oriented non-valid path genome. At least m cycles of  have to be merged in the path to make it valid.
have to be merged in the path to make it valid.
An edge  or
or  of the adjacency graph
of the adjacency graph  is called oriented if markers x and
is called oriented if markers x and  have different signs. Note that extracting a cycle from any element of the graph
have different signs. Note that extracting a cycle from any element of the graph  requires this element to contain oriented edges. It is easy to see that given two adjacencies picked in a given element, a reversal acting on these adjacencies will extract a cycle if and only if the path linking these adjacencies contains an odd number of oriented edges. Thus, we have the following lemma:
requires this element to contain oriented edges. It is easy to see that given two adjacencies picked in a given element, a reversal acting on these adjacencies will extract a cycle if and only if the path linking these adjacencies contains an odd number of oriented edges. Thus, we have the following lemma:
Lemma 3
Let G be an oriented non-valid-path genome. Merging a cycle of
 in its path never creates unoriented connected components in the overlap graph of the genome obtained.
in its path never creates unoriented connected components in the overlap graph of the genome obtained.
Proof. See proof in Additional file 1 (Supplemental proofs). ■
Theorem 3 Let G be an oriented non-valid-path genome. Let C be the number of cycles in the graph and m be the minimum number of cycles to merge in the path to make it valid. The reversal dedoubling distance of G is d
rev
(G) = n – C + 2m.
and m be the minimum number of cycles to merge in the path to make it valid. The reversal dedoubling distance of G is d
rev
(G) = n – C + 2m.
Proof. See proof in Additional file 1 (Supplemental proofs). ■
Prom Lemma 1 and Property 2, the complexity of the Genome Dedoubling problem by reversal on oriented genomes follows immediately.
Corollary 3 The Genome Dedoubling problem by reversal on oriented genomes is NP-complete. Algorithm 2 solves the problem in quadratic time complexity, except for the computation of S i that is 2-approximable.
Application
We applied Algorithm 2 to reconstruct an ancestral chromosome for the chromosome 2 of Drosophila yakuba using a dataset obtained from [4] with Drosophila melanogaster used as the outgroup. The results obtained are in good agreement with the biological results explaining the evolution of the chromosome 2 from Drosophila yakuba to Drosophila melanogaster in the litterature [4, 15]. See Additional file 2 (Experimental results) for a description of the dataset and the results of the application.
Conclusion
In this paper, we introduced the genome dedoubling problem in the DCJ rearrangement model, NP-complete in both the multichromosomal and the linear unichromosomal case, by reduction to an APX-complete problem. For both cases, we described an algorithm solving the problems in linear time complexity, except for an APX-complete part that is 2-approximable. We also presented some results on the Genome Dedoubling problem by reversal, providing an algorithm solving the problem on oriented genomes in quadratic time complexity, except for an APX-complete part that is 2-approximable. The case of unoriented genomes in the reversal model will be treated in a future paper. Unsurprisingly, partial results obtained so far tend to show that the general distance formula can be written as d
rev
(G) = n – C + 2m + t, with t corresponding to the cost of genome orientation. However, the cost t here differs from the orientation cost described in the classical reversal theory based on the unoriented component tree [14]. In our case, the structure of the graph  allows to orient components while not decreasing the number of cycles, or even increasing it in some cases. This requires proper identification of different kinds of merging reversals and further extensions on the data structures presented in this paper.
allows to orient components while not decreasing the number of cycles, or even increasing it in some cases. This requires proper identification of different kinds of merging reversals and further extensions on the data structures presented in this paper.
The second obvious extension of the present work, as in the the Genome Halving problem theory [16], is to generalize the Genome Dedoubling problem defined on a single genome, to the Guided Genome Dedoubüng problem, that asks to find a non-duplicated genome that minimizes the breakpoint-duplication distance to a given duplicated genome, plus the distance to a given non-duplicated genome. A further extension of this work consists of taking account of the degree of divergence of the breakpoint-duplicated sequences to order the rearrangement operations in time as done in [10].
References
Samonte R, Eichler E: Segmental duplications and the evolution of the primate genome. Nature Reviews Genetics 2002, 6: 65–72.
Armengol L, Pujana M, Cheung J, Scherer S, Estivill X: Enrichment of segmental duplications in regions of breaks of synteny between the human and mouse genomes suggest their involvement in evolutionary rearrangements. Human Molecular Genetics 2003, 12(17):2201–2208. 10.1093/hmg/ddg223
Bailey J, Baertsch R, Kent W, Haussler D, Eichler E: Hotspots of mammalian chromosomal evolution. Genome Biology 2004, 5(4):R23. 10.1186/gb-2004-5-4-r23
Ranz J, Maurin D, Chan Y, Von Grotthuss M: Principles of genome evolution in the Drosophila melanogaster species group. PLoS biology 2007, 5(6):e152+.
Matzkin L, Merritt T, Zhu CT, Eanes W: The structure and population genetics of the breakpoints associated with the cosmopolitan chromosomal inversion In(3R)Payne in Drosophila melanogaster. Genetics 2005, 170: 1143–1152. 10.1534/genetics.104.038810
Richards S, Liu Y, Bettencourt B, Hradecky P, Letovsky S: Comparative genome sequencing of Drosophila pseudoobscura: Chromosomal, gene, and cis-element evolution. Genome Research 2005, 15: 1–18. 10.1101/gr.3059305
Meisel R: Repeat mediated gene duplication in the Drosophila pseudoobscura genome. Gene 2009, 438(1–2):1–7. 10.1016/j.gene.2009.02.019
Quinlan A, Clark R, Sokolova S, Leibowitz M, Zhang Y, Hurles M, Mell J, Hall I: Genome-wide mapping and assembly of structural variant breakpoints in the mouse genome. Genome Research 2010, 20: 623–635. 10.1101/gr.102970.109
Howarth KD, Pole JCM, Beavis JC, Batty EM, Newman S, Bignell GR, Edwards PAW: Large duplications at reciprocal translocation breakpoints that might be the counterpart of large deletions and could arise from stalled replication bubbles. Genome Research 2011, 21(4):525–534. 10.1101/gr.114116.110
Lemaitre C, Braga M, Gautier C, Sagot MF, Tannier E, Marais G: Footprints of Inversions at Present and Past Pseudoautosomal Boundaries in Human Sex Chromosomes. Genome Biology 2009, 1: 56–66.
El-Mabrouk N, Nadeau J, Sankoff D: Genome Halving. In In proc. of Combinatorial Pattern Matching. LNCS 1448. Springer; 1998:235–250.
Hannenhalli S, Pevzner PA: Transforming Men into Mice (Polynomial Algorithm for Genomic Distance Problem). In In proc. of FOCS 1995. IEEE Press; 1995:581–592.
Bergeron A: A very elementary presentation of the Hannenhalli-Pevzner theory. Discrete Applied Mathematics 2005, 146(2):134–145. 10.1016/j.dam.2004.04.010
Bergeron A, Mixtacki J, Stoye J: Reversal distance without hurdles and fortresses. In In proc. of Combinatorial Pattern Matching. LNCS 3109. Springer-Verlag; 2004:388–399.
Lemeunier F, Ashburner M: Relationships within the melanogaster species subgroup of the genus Drosophila (Sophophora). II. Phylogenetic relationships between six species based upon polytene chromosome banding sequences. Proceedings of the Royal Society of London, Series B, Biological Science 1976, 193(1112):275–294. 10.1098/rspb.1976.0046
Zheng C, Zhu Q, Sankoff D: Genome halving with an outgroup. Evolutionary Bioinformatics 2006, 2: 319–326.
Berman P, Fujito T: Approximating independent sets in degree 3 graphs. In In proc. of Workshop on Algorithms and Data Structures. LNCS 955. Springer-Verlag; 1995:449–460.
Hochbaum DS: Efficient bounds for the stable set, vertex cover and set packing problems. Discrete Applied Mathematics 2004, 6: 243–254.
Acknowledgements
We would like to thank Anne Bergeron for her useful comments on the breakpoint-duplication phenomenon, and the anonymous reviewers of the paper for their useful comments on the first version of the document.
This article has been published as part of BMC Bioinformatics Volume 12 Supplement 9, 2011: Proceedings of the Ninth Annual Research in Computational Molecular Biology (RECOMB) Satellite Workshop on Comparative Genomics. The full contents of the supplement are available online at http://www.biomedcentral.com/1471-2105/12?issue=S9.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
The work was divided in four steps: 1) Formal introduction and reduction of the Genome Dedoubling problem. 2) Design of the study. 3) Study of the Genome Dedoubling problem by DCJ. 4) Study of the Genome Dedoubling problem by reversal on oriented genomes. AT participated in 2) and 3), and carried out 4). JSV participated in 2), 3) and 4). AO carried out 1), 2) and 3), and participated in 4). All authors participated in writing the manuscript, and approved the final manuscript.
Electronic supplementary material
12859_2011_4827_MOESM1_ESM.pdf
Additional file 1: Supplemental proofs Additional file 1 is a PDF file containing the proofs of Proposition 3, Property 1, Lemma 1, and Property 3. (PDF 241 KB)
12859_2011_4827_MOESM2_ESM.pdf
Additional file 2: Experimental results Additional file 2 is a PDF file containing a description of an application of the methods to real Drosophila data. (PDF 163 KB)
Rights and permissions
Open Access This article is published under license to BioMed Central Ltd. This is an Open Access article is distributed under the terms of the Creative Commons Attribution License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Thomas, A., Varré, JS. & Ouangraoua, A. Genome dedoubling by DCJ and reversal. BMC Bioinformatics 12 (Suppl 9), S20 (2011). https://doi.org/10.1186/1471-2105-12-S9-S20
Published:
DOI: https://doi.org/10.1186/1471-2105-12-S9-S20
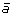 at the appropriate position to produce segment
at the appropriate position to produce segment 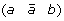 ,
,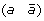 and (c d) to produce either (a d) and
and (c d) to produce either (a d) and 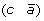 , or (a –c) and
, or (a –c) and  .
. and
and 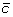 at the appropriate positions to produce segments
at the appropriate positions to produce segments 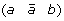 and
and 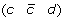 ,
,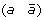 and
and 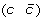 to produce either
to produce either 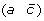 and
and 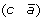 , or (a –c) and
, or (a –c) and 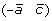 .
.
 .
.
 . Oriented vertices are colored in grey. The graph
. Oriented vertices are colored in grey. The graph  has two connected components, one oriented and one unoriented. b. the overlap graph obtained after applying the reversal
has two connected components, one oriented and one unoriented. b. the overlap graph obtained after applying the reversal  to produce adjacency
to produce adjacency .
.
