- Research article
- Open access
- Published:
Entropy-based gene ranking without selection bias for the predictive classification of microarray data
BMC Bioinformatics volume 4, Article number: 54 (2003)
Abstract
Background
We describe the E-RFE method for gene ranking, which is useful for the identification of markers in the predictive classification of array data. The method supports a practical modeling scheme designed to avoid the construction of classification rules based on the selection of too small gene subsets (an effect known as the selection bias, in which the estimated predictive errors are too optimistic due to testing on samples already considered in the feature selection process).
Results
With E-RFE, we speed up the recursive feature elimination (RFE) with SVM classifiers by eliminating chunks of uninteresting genes using an entropy measure of the SVM weights distribution. An optimal subset of genes is selected according to a two-strata model evaluation procedure: modeling is replicated by an external stratified-partition resampling scheme, and, within each run, an internal K-fold cross-validation is used for E-RFE ranking. Also, the optimal number of genes can be estimated according to the saturation of Zipf's law profiles.
Conclusions
Without a decrease of classification accuracy, E-RFE allows a speed-up factor of 100 with respect to standard RFE, while improving on alternative parametric RFE reduction strategies. Thus, a process for gene selection and error estimation is made practical, ensuring control of the selection bias, and providing additional diagnostic indicators of gene importance.
Background
The study of gene expression patterns is expected to enable significant advances indisease diagnosis and prognosis. The main objectives of a discovery process based on microarray data are the understanding of the molecular pathways of diseases, their early detection, and the development of measures of individual responsiveness to existing or new therapies. In particular, the perspective of providing new targets for therapy and of developing clinical biomarkers has given a strong impulse to methods for ranking genes in terms of their importance as predictor variables in the construction of classification models from arrays [1–6].
In this paper, we address the problem of developing a practical methodology for gene ranking based on the support vector machine classifier (SVM), a machine learning method that is considered particularly suitable in the classification of microarray data [7–9]. A typical prediction task for the methodology would be the identification of patients resistant to a therapy or the definition of a 'terminal signature', a set of genes and a decision rule identifying short-term survivors who might benefit from specific therapies [10, 11]. For example, recent results have shown that the clinical outcomes of high grade gliomas [12] and of cutaneous T cell lymphoma [11] may be better identified by gene expression-based classification than by histological classification or measures of tumor burden.
The methodology described in this paper is designed to obtain a list of candidate genes, ranked for importance in discriminating between classes, and the corresponding SVM classification model. The method also provides an honest estimate of the model accuracy on novel cases (predictive accuracy).
Feature elimination for SVM
We have developed the entropy-based recursive feature elimination (E-RFE) as a non-parametric procedure for gene ranking, which accelerates – without reducing accuracy – the standard recursive feature elimination (RFE) method for SVMs [6]. The RFE procedure for SVM has been evaluated in experimental analyses [13] and it is considered a relevant method for gene selection and classification on microarrays. However, RFE for SVM has high computational costs. At each model building step, a pair (classifier, ranked gene set) is constructed from samples in a training set and evaluated on a test set, where training and test are subsets of the data available for development at this step. The contribution of each variable is defined through a function of the corresponding weight coefficient that appears in the formula defining the SVM model. The elimination of a single variable at each step (as in the basic RFE procedure) is, however, inefficient. In a typical microarray study, thousands of genes have very low SVM weights in the initial steps. An alternative is the simultaneous removal of a fixed fraction of the genes (decimation) or according to a parametric rule (e.g. the square root function). These basic, parametric, acceleration techniques or gradient based methods have been proposed in machine learning studies [6, 14, 15], showing that accuracy close to basic RFE may be obtained.
The aim of our E-RFE procedure is to provide a more flexible feature elimination mechanism in which the ranking is obtained by adaptively discarding chunks of genes which contribute least to the SVM classifier. In our E-RFE method, we cautiously discard, according to the entropy of the weight distribution, several (possibly many) genes at each step to drive the weight distribution in a high entropy structure of few equally important variables (see Methods for details). The procedure should accommodate for the different SVM weight distributions arising from supervised classification tasks on different microarray data.
The selection bias problem
As shown in the Results section, the E-RFE method achieves a speed-up factor of 100 with respect to RFE. It also produces a faster and more flexible gene elimination curve than parametric versions of RFE. Finally, feature elimination with E-RFE does not significantly degrade accuracy with respect to the slower, one-step RFE.
These results have allowed us to adopt E-RFE for SVM as the basis for a complete methodology scheme for gene selection designed to control the "selection bias". This bias causes a methodology flaw which is easily introduced within gene selection procedures that depend on the optimization of a classification rule ("wrapper" algorithms). While this flaw can be reproduced with any wrapper algorithm, the selection bias is a specific risk for RFE-SVM gene selection procedures.
To separate the feature-selection process from the performance assessment, the bias has to be corrected in the estimates of prediction error whenever the selected model is tested on data previously used to find the best features [16]. This occurred in several early studies on microarrays that discovered very few genes yielding classification models with negligible or zero error rates ("perfect" or "near-perfect" classification with very few genes on arrays of dozens of subjects and up to 20 000 genes). The flaw unfortunately leaked into the original work on RFE, and it is still being replicated in different supervised machine learning approaches [17]. A typical contamination pattern is the following. Consider a data set S and its three subsets S0, S1, and S2. Suppose that the best feature set is obtained on S0, e.g. composed by the features of a classification model with minimum cross-validation (CV) error estimated on S0. The correct methodology requires that a model with the optimal features is then trained on S1 and tested on S2 to obtain an error estimate for new cases. But if the test data set S2 overlaps with the S0 used in the selection process, even for disjoint S1 and S2, an over-optimistic error rate will be estimated on S2, possibly leading to the conclusion that a panel of very few genes is adequate to differentiate between classes. In particular, over-optimistic error rates are being produced when the S2 hold-out set is not available and the CV error is computed on a part of S0 ∪ S1.
A flawed scheme can be assessed by developing models on no-information data, i.e., by a random permutation of class labels. Errors on a disjoint test set should result close to the no-information error rate – approximately 50% on a balanced data set in a binary classification task. Instead, whenever the error is estimated on data previously used in the feature selection process, a CV error close to zero can be obtained with a small subset of genes even if a classifier is trained on data with class labels randomly permuted, (see [16, 17] and the synthetic and real examples in the Results section in this paper).
Validation scheme
A more sophisticated experimental design is thus needed to validate the performance of diagnostic methods based on supervised class prediction rules on gene expression data. An unbiased error estimation for models developed on a reduced number of biomarkers must be obtained from an external process operating out-of-sample from the data involved in the selection process [18, 17]. Two strata of processes have to be considered, an external one for performance assessment and an internal one for feature selection. At each level, a resampling and partition method has to be applied, to smooth data variability and balance class cardinalities.
The methodology scheme we propose for the validation of supervised methods belongs to this family of experimental designs and it is summarized in Fig. 1. The scheme can be applied to alternative feature ranking procedures, such as the penalized discriminant analysis (PDA) [19, 11]. It can also be used with SVM in conjunction with other gene filters based on statistical tests (the correlation coefficients [20], and the T-score filters [8, 16, 21, 6, 5, 14]; see implementation in Results).
The methodology scheme. In order to avoid the selection bias, an external resampling scheme (stratified partitioning) is coupled to an internal K-fold cross-validation applied to the ranking method under study. The modeling procedure is replicated on resampled versions of the original data set, with validation always operated on a test set disjoint from the development material (dev) for the current run (VAL procedure). Modeling and feature ranking are computed by the internal OFS-M procedure (e.g. a SVM for each E-RFE or RFE step). Within OFS-M, the procedure ONF is designed to estimated the optimal number of features at the saturation of a Zip's law.
A crucial problem is that this kind of designs requires an intensive replication of classifier builds, leading to a tradeoff between feasible computation times and the level of sophistication in the development of the overall gene selection process.
The availability of such a bias-correcting scheme also has an important implication for gene panel sizes. A monotonic and exponential-like decrease of predictor accuracy is typically found for increasing numbers of genes when the complete method is used, and perfect classification is rarely achieved with very small sets of genes. No intrinsic cutoff for gene selection is thus automatically provided by the classification models. The observation led us to adopt a Zipf's power-law hypothesis for gene selection [22]. We have thus used a strategy for gene selection that is based on a saturation profile derived from an exponential approximation of the classification error, as estimated by the two-strata modeling scheme.
Results
The effect of selection bias on synthetic data
We set up two experiments on synthetic data in order to elucidate the need for a complex methodology scheme, as indicated in [17]. We considered first the dataset f1000–5000, structured as follows: 100 samples described by 5000 features, in which 1000 of them are significant (i.e. generated by 1000 Gaussian distribution centered in 1 and -1, with standard deviation uniformly ranging between 1 and 5), and the remaining are uniform noise in the range [-2,2]. We first applied the RFE feature ranking procedure to the whole dataset. The importance of features for discrimination was then evaluated by creating a sequence of SVM models based on an increasing number of features (every single step at 1–15 genes, every 5 at 15–50, every 10 at 50–200, every 100 at 200–1000; further details are given in Methods). The performance was evaluated by a 10-fold CV procedure (one tenth of the data held out and used for testing in turn, test results averaged).
In Figure 2(a) we represent the average CV error over the ten experiments: the selection bias effect is shown by the f1000–5000 curve (solid line), which reaches a zero CV error with only 9 features. Note that the error raises using 11 variables, and it is definitely zero for 12 or more variables.
Subfigure 2(a): Synthetic data. Subfigure 2(b): Colon cancer. Comparison of leave-one-out error curves for synthetic data and real data sets. The model error is computed on the data previously used for ranking. On synthetic data (a), the RFE-SVM method achieves perfect classification with 9 of the 1000 relevant features (solid line) in data set f1000–5000. Moreover, 20 features are sufficient to reach perfect classification on the purely noisy data set f0–5000 (dashed-dotted line). In the right panel (b) for the Colon cancer data from ref. [23], similar error estimates are obtained for the real data (perfect classification with 8 genes – solid curve) and with randomized labels (dashed curve), for which 14 genes are sufficient to get a zero error estimate.
We set up a second data set of 100 samples described by 5000 uniform noise features in the range [-2,2]. We applied the RFE feature ranking procedure to the whole dataset and then we performed a 10-fold CV with different feature subsets. In Figure 2(a), the f0–5000 curve (dashed-dotted line) displays the average CV error over the 10 experiments. The selection bias effect can be read on the obtained curve which shows a zero CV error with only 20 features. This is an even clearer example of the selection bias effect: the features consist of pure noisy data (and thus not separable at all), nevertheless the classifier indicates some of them as relevant, reaching a 100% accuracy.
The effect of selection bias on real data
The potential for inducing the bias in a class prediction study can be shown for the the colon cancer microarray data set from [23]; the set consists of expression levels of 2000 genes from 62 tissues (22 normal and 40 tumor cases, Affimetrix oligonucleotide arrays). The RFE error curves shown in the right plot of Figure 2(b) were estimated by leave-one-out cross-validation for models trained on feature subsets of increasing size, after a feature ranking performed on all the available data. The same data were used for development and test: as a consequence a zero error was obtained with only 8 genes (solid curve). Surprisingly, when the procedure was applied to the same data after a label randomization, a very similar result was obtained without any class information: 14 genes were sufficient for a zero leave-one-out error estimate (dashed line). This behavior was replicated by using the other ranking methods we describe below.
Entropy-based ranking of microarray data
We tested the E-RFE ranking approach (see below) on three well known data sets: (i) a colon cancer data set [23], (ii) a lymphoma data set of 96 samples (72 cancer and 24 non cancer, cDNA) described by 4026 genes [24], and (iii) a tumor vs. metastases data set, consisting of expression levels of 16063 genes describing 76 samples (64 primary adeno-carcinomas and 12 metastatic adeno-carcinomas, Affimetrix oligonucleotide arrays) [13, 10]. The original public data were subjected to the following preprocessing across genes: the vector of the expression values of every gene was linearly rescaled to mean zero and standard deviation one. We analyzed the properties of E-RFE by considering the effect of recursive feature elimination on the distribution of the weights in the SVM model.
In Figures 3(a)–3(c), referring to the tumor vs. metastases data, we show how the distribution of the SVM weights is modified by the entropy-based selective gene elimination. At the beginning of the feature elimination process, the construction of a SVM on the complete set of features on the tumor vs. metastases data produces a large amount of weights w whose cost function J (α) is concentrated nearby zero (see Methods for the definition of J (α)). The result is displayed in Figure 3(a): the n = 16063 J (α) values, normalized in the unit interval, are plotted in the left panel, and their frequencies are stratified at 1/ bin width in the right panel.
bin width in the right panel.
With the one-step RFE algorithm, just one of the features with negligible weight would be removed, while it would be more efficient to eliminate a chunk of the lowest ranking genes. On the other hand, eliminating genes at fixed steps, or according to a specific parameterization introduces the problem of making assumptions on the SVM weight distribution, which may be specific of the microarray data set. A process based on the entropy measure (defined by Eq. 1 in Methods) allows to eliminate chunks of uninteresting genes until the remaining distribution stabilizes in a higher entropy regime of the weight distribution, adapting to the characteristics of the microarray data at hand.
Speedup of E-RFE
As described below, in E-RFE procedure we apply different strategies for weight removal, according to a comparison of the current entropy H and of the mean M of the weight distribution with two thresholds H t and M t , respectively.
For the low entropy structure with n = 16063 genes in Figure 3(a), 5678 genes are eliminated at Step 1. In 10 reduction steps we obtain a classification model based on 1293 features (Figure 3(b)). The distribution is still characterized by many low weight values, which are selectively removed by E-RFE: at Step 17 (Figure 3(c)) a subset of 315 genes is obtained, with a high entropy and less concentrated distribution. Only 15 genes will be eliminated.
Let us consider also a parametric feature elimination in which the leftmost bin of

features is removed at each step (SQRT-RFE method). In Figure 4 the number of steps required by the E-RFE and SQRT-RFE methods on the tumor vs metastases data set are compared along with the number of undiscarded features at each step. The E-RFE procedure is much faster in this task, as detailed in Table 1 for the three microarray data sets. Similar results were found for the other datasets.
Accuracy of E-RFE
We analyze now the accuracy of the E-RFE and SQRT-RFE methods as compared to the basic RFE procedure on the colon cancer and lymphoma data sets. We also considered two filter ranking methods, the Correlation Coefficients (CC) in the version of [20], and the T-score method (TT), previously applied to these data by different authors [8, 16, 21, 6, 5, 14]. In the tumor vs. metastases data set only the E-RFE and SQRT-RFE methods were employed due to computational feasibility reasons. Classification errors were estimated by a random partition resampling scheme over 50 repeated experiments, with a development-test splitting, in proportion of 3/4–1/4, and preserving the proportion of positive and negative cases for each set. For each resampling, the five ranking methods were applied to each development set, and linear SVMs were trained using the ranked subsets of features. The performance was then estimated on the independent test set, and finally averaged over the runs. A full description of the experimental scheme, designed to correct the effect of the selection bias, is given in Methods.
In Tables 2, 3 and 4 we report the average test errors of SVMs for gene subsets of increasing car-dinality for each data set. Very close errors and standard deviations are estimated for E-RFE and RFE: accuracy is thus preserved even though the E-RFE algorithm is much faster (about 100 steps instead of 2000 on colon cancer, about 120 instead of 4026 on lymphoma and 116 instead of 16063 for the tumor vs. metastases dataset). In general, for gene subsets of fixed size, no significant difference is detected among the RFE-based methods on the three datasets (t-test at 95% confidence level, df = 49). A significant difference is found between the RFE-based methods and the CC or TT methods for less than 300 genes.
An error estimate with a correction of the selection bias is shown in Figure 5(b). Given a development/test split of the data, we considered an internal K-fold cross-validation experiment on the development data only. For K = 3, two thirds of the development data were used at each cross-validation step to build SVM models on feature sets of increasing size ranked by the selected method. Models were then tested on the remaining third of the development data. The error curve in Figure 5(b) is estimated by averaging over the CV test sets. The error does not reach zero, but it exhibits a rapidly decreasing pattern which suggests an exponential behavior (fit shown by a solid line).
Subfigure 5(a): Global model; Subfigure 5(b): Run 40: Estimated 3-fold error curves for E-RFE models trained on feature sets of increasing size and without any use of test data in feature ranking (experimental run 40 of 50 on colon cancer). In each plot, the solid curve is an exponential fit, while the saturating n* is indicated by a dotted line.
Such a pattern can be used to implement a feature selection procedure convenient for microarray studies. We have analyzed the results obtained by applying an optimal number of features (ONF) procedure designed to compute an approximate estimate of the optimal number of features n* for microarray data sets. Based on a K-fold experimental structure, the cross-validation error curve is fitted by an exponential map and n* is chosen as the point where the error difference with the next point along the fit is less than 1/1000 of the error range (see dotted line in Figure 5(b); details are given below).
In Table 5 we show the results of the OFS-M procedure application for a feature selection process where the SVM models were developed for E-RFE and RFE on the complete colon cancer, lymphoma and tumor vs. metastases data sets, respectively. For comparison, the OFS-M procedure was also applied with CC, TT and SQRT-RFE feature rankers and SVM classifiers. For the colon cancer data set, the optimal numbers of features are similar for the RFE-based methods (E-RFE, RFE, SQRT-RFE) and greater than those for CC and TT. On the other two data sets, no significant differences were found.
The complete methodology scheme introduced in Fig. 1 was applied to evaluate the predictive accuracy of the model obtained by the application of the OFS-M procedure. We plugged the previous experiment within the more complex validation (VAL) procedure, detailed below. For each of the three microarray data sets, 50 development/test splits were considered, and the ONF procedure was replicated: on each of the b = 1,...,50 development sets, we used an internal 3-fold cross-validation for feature ranking and estimation of the error curve and of the n*boptimal number of features. In Table 6, we report the average error on the independent test sets, and the average  , the average of the 50 n*b. On the colon cancer data, the optimal number of features was higher for E-RFE, RFE and SQRT-RFE (about 70 against 50 for CC and TT), but more accurate models were obtained. The test error was close to 18% for the three wrapper methods and greater than 20% for the two filter ones. On the lymphoma data, the mean expected number of features resulted 80 for all methods, but with a lower test error for the RFE-based methods. For the tumor vs. metastases data set all the obtained results are similar regardless of the method employed.
, the average of the 50 n*b. On the colon cancer data, the optimal number of features was higher for E-RFE, RFE and SQRT-RFE (about 70 against 50 for CC and TT), but more accurate models were obtained. The test error was close to 18% for the three wrapper methods and greater than 20% for the two filter ones. On the lymphoma data, the mean expected number of features resulted 80 for all methods, but with a lower test error for the RFE-based methods. For the tumor vs. metastases data set all the obtained results are similar regardless of the method employed.
 : average optimal number of features).
: average optimal number of features).Diagnostics of E-RFE
Providing a measure of relative importance of genes in the classification problem is a central product of gene ranking procedures. For each of the genes selected in the optimal feature sets over the total data as produced by E-RFE (80 features for colon cancer and 70 for the other two datasets), we compared the SVM weights with the number of extractions in the optimal gene subsets (gene multiplicity) as resulting from the replicated experiments. Figure 6 shows the number of extractions of the i-th feature in replicated experiments vs the weight function f w (i) = max i (|w i |) - |w i | obtained by the SVM model with optimal number of features. The points in the upper part of the figure indicate variables not chosen in the global model, but extracted in at least one run; the features labeled by a capital Latin letter are those extracted at least 25 times (threshold indicated by the dotted line) in the replicated experiments.
Subfigure 6(a): Colon cancer; Subfigure 6(b): Lymphoma; Subfigure 6(c): Tumor vs. metastases. The accumulated number of extractions (gene multiplicity) in 50 replicated runs is compared to the f w weight ranking function for features selected by the E-RFE model trained on the whole data set at n* features. The groups of isolated points in the upper part of the panels indicate variables in the optimal feature sets for the replicated and not extracted in the global model. The variables labeled by capital Latin letter are those extracted more than 25 times in the replicates. The dotted line marks the 25 extractions threshold.
We performed a simulation to examine the stability of the gene multiplicity rank for E-RFE. We considered two synthetic data sets, each of 100 cases (50 labeled 1 and 50 labeled -1) described by 1000 features: the 1000 features in U1 were all uniformly distributed in the interval [-2,2] and thus not discriminating the classes. The second data set U2 was derived from U1 by keeping unvaried 995 features and introducing 5 features normally distributed with mean 1 or -1 according to class, and variance 1.5.
In Figure 7(A),7(B),7(C) we display the distribution of the feature normalized position for the first 5 variables according to the multiplicity rank computed over 50 replicated runs for datasets U1, U2 and colon cancer, respectively. Let r(v,b) be defined as the rank of v at run b, and n*bthe optimal estimated number of features for the colon cancer microarray at run b. The feature normalized position of feature v at run b is then defined as ν (v, b) = 1 - ((r(v, b) - 1) / n*b), if r ≤ n*b, and ν (v, b) = 0, otherwise. In practice, at run b, ν(v, b) is maximal when v has rank 1, and minimal when v is the last of the  features considered.
features considered.
Subfigure 7(A): U 1 ; Subfigure 7(B): U 2 ; Subfigure 7(C): Colon cancer. A comparison of multiplicity ranks for E-RFE for two synthetic data sets (A: no relevant variables; B: 5 relevant variables) and (C) colon cancer microarray data. In each panel, the boxplots indicate the distribution of the feature normalized position ν (see text for the definition) for the 5 highest rank features.
The first 5 features for the no-information synthetic data set U1 in Figure 7(A) are in the lowest half of the range of ν. High scores may be produced by randomization at single b runs, but the rank is not steadily maintained throughout the 50 replicates. On the contrary, exactly the 5 relevant features of the synthetic data set U2 obtain the first multiplicity E-RFE ranks, with a limited variability, shown in Figure 7(B). Thus the highest ranks are constantly confirmed in the synthetic data set. The top 5 genes for the real data set displayed in Figure 7(C) have a behavior much similar to the 5 relevant variables from U2, with more variability.
In Tables 7 and 8 (respectively for colon cancer and lymphoma data), for each of the labeled points of the Figure 6, we report the gene name (Gene Accession Number for colon cancer and Clone number for lymphoma) and the  weight ranking. We also report the gene multiplicity, i.e. the number of replicated experiments in which the gene was in the optimal feature set. In Table 8, the E-RFE ranking instead of the w
score
function is reported for variables not selected in the global model and indicated by a letter in Figure 6.
weight ranking. We also report the gene multiplicity, i.e. the number of replicated experiments in which the gene was in the optimal feature set. In Table 8, the E-RFE ranking instead of the w
score
function is reported for variables not selected in the global model and indicated by a letter in Figure 6.
Finally, random permutations of class labels were produced as described in Methods to detect additional overfitting effects. The E-RFE procedure was then applied and the mean error was computed for subsets of increasing size. In Figure 8 we report the comparison between test error curves on true and random labels for colon cancer and lymphoma. The error on randomized classes is close to 40% or above; a paired t-test confirmed significant difference (p = 0 for all experiments) between mean accuracy over random and true labels data. It is worth noting that the error is less than 50% because of the unbalanced proportion of classes.
Discussion
The best prediction accuracy on the colon cancer and lymphoma microarray data sets is obtained with more than 50 genes. The estimated error is less than 20% for the colon cancer data, and less than 5% for lymphoma. For the tumor vs. metastases dataset, we obtain an error lower than 14% by using more than 300 variables. These results are consistent with recently published work using a similar experimental schemes [16], while they differ from results of perfect or near-perfect classification with very few genes. Also considering the results of the experiments with no-information data, we may conclude that several promising results on microarray data may be descriptive of the shattering properties of classifiers on the given microarray data sets [18, 16, 17].
The exponentially decreasing behavior we observed after correcting for selection bias is consistent with recent literature proposing that the relationship between cancer classification accuracy and gene ranking from microarray data may be modeled by a power-law function, also called a Zipf's law [22, 25]. The exponential fit in the ONF procedure and the power-law functions are rough but working approximations for microarray data. In our experience, the choice of a cutoff based on a Zipf's law fit was less accurate than applying ONF with the exponential fit.
The ONF procedure defined by the exponential fit allows the identification of a saturating number of genes. The gene-ranking procedure can also be used to select larger or smaller subsets of genes as biomarkers, according to practical considerations. The validation procedure provides an error estimate for the selected subset in these cases. The ONF procedure was developed for the recursive feature elimination with SVM classifiers, and it results less accurate with the basic CC and TT filter approaches. A similar strategy similar to ONF is described in [26].
The VAL procedure allowed the estimation of model accuracy, optimal number of features, and a ranking of the most important features on the three microarray data sets. The entropy-based method E-RFE for the recursive feature elimination process showed results comparable with the more time consuming RFE and SQRT-RFE. The running times for a complete feature ranking process on a Pentium III 1 GHz processor are reported in Table 1 for all data sets. Proportional results were found for computations run on an Open-Mosix cluster. The accelerated E-RFE method therefore allows the standard use of complex model-evaluation and model-selection schemes.
On colon cancer data, all the variables extracted more than 25 times in the replicated experiments are contained in the list obtained by the global model. For the lymphoma data, all genes with multiplicity greater than 25 ranked within the first 165 genes of the global model, and only 8 were not in the selected set of 70 genes. Finally, in the tumor vs. metastases data set, only two features extracted more than 25 times are not included in the 70 genes optimal feature set, but they rank 84th and 89th in the reordered list.
Together with the rank based on SVM weights, gene multiplicity provides an additional measure of importance for the extracted genes. A good correspondence between the two indicators was found for the highest ranked genes. In a simulation study, gene multiplicity allowed the identification of the only relevant genes; moreover, the best ranked genes in simulation and on real data seem to maintain stability in the estimated rank. This property might be exploited in future comparisons of ranked lists produced by different ranking and classification methods.
Comparing Table 7 with other published work on the colon cancer data, two genes (numbered as 20 and 42 in the table) were also cited in the original study [23]. Moreover, twelve genes (5, 9, 10, 21, 25, 34, 37, 44, 46, 56, 71, 73) are also listed as important in [21], four genes (9, 10, 22, 26) in [6], three genes (5, 9, 44) in [2], and 9 genes (5, 9, 21, 22, 28, 34, 44, 57, 71) in [4].
In all our experiments, the use of linear SVM was accurate enough and provided faster performance than kernel-based SVM. Thus we did not introduce methods for kernel-based selection. However the scheme can be used to test models defined by different SVM architectures.
As alternatives to the ranking methods discussed in this paper in association to SVM supervised models, several other procedures are available to researchers. In a similar framework, the PDA based software CLEAVER [27] can be used in a combination of supervised classification and gene ranking. In [11], the authors based a first reduction of the number of genes on the t-test, one of the most used strategies for gene filtering. Variation filters and signal-to-noise ratio, also used together with random permutation testing, are other valid alternatives [12].
While attempting to reproduce results from other authors, we noticed the existence of a "preprocessing bias", also mentioned in [16]. The bias appears to originated with the application of ad-hoc strategies for reducing the effect of outliers. We decided to adopt the standard normalization for all data sets in our experiments. For instance, in the colon cancer example, due to the lack of additional independent data, we choose not to apply any squashing function optimized for outlier control. In developing diagnostic methods for microarray data, an additional adaptation to test data may be hidden in the choice of the normalization procedures and parameters. The methodology scheme implemented for E-RFE might be a candidate system for an unbiased estimate of the optimal preprocessing metaparameter related with the predictive model structure.
Conclusions
The new E-RFE algorithm was designed to estimate the relative importance of genes, with applications for predictive classification on array data. The algorithm is shown to preserve the accuracy achieved by the SVM classifier by using other ranking methods. At the same time it achieves a significant reduction of the computational workload. This result is crucial because high-throughput data analysis must also include the resampling procedures needed to ensure an honest estimate of accuracy and thus to avoid a gene selection process mainly driven by overfitting.
In order to correctly deal with the problem, we have developed an experimental set-up for analysis and prediction on microarray data. This set-up has allowed us to correctly identify the impact of the selection bias on synthetic and real data sets.
By controlling the risk of overoptimistic predictions, which have affected a number of recently published works, this set-up has provided a support for the identification of the function which associates prediction accuracy to the number of genes. On this basis, we have also pointed out a strategy for the individuation of a saturating subset of genes.
A basic advantage of the E-RFE method, within the experimental set-up we have adopted, is the automatic adaptation to the different weight distributions coming from prediction models developed from different DNA chips. Automatic model selection based on an extension of E-RFE may become of further interest for the integrated treatment of all the phases of the array analysis, including the selection of parameters for data normalization purposes.
Finally, it is important to start investigating new diagnostic criteria for the comparison and possibly the combination of ranked lists of genes computed from different supervised methods on the same array data.
Methods
Model selection and assessment
The experimental set-up proposed in this paper is partially similar to those described in [5, 16], and it may be summarized as an external stratified partition resampling scheme coupled with an internal K-fold cross-validation, to be applied to E-RFE or to other feature ranking methods at each run. This intensive double model selection and error estimation process is graphically outlined in Figure 9. The method is composed by three main blocks:
OFS-M procedure (Figure 9(a)): given a training set TR, a feature ranking method produces a list of ranked features RF, from which an optimal feature set OFS of size n* is selected. Based on OFS, a model M is developed by a suitable learning method. The optimal number of features n* is computed by the ONF procedure, while the accuracy of OFS-M is to be validated by the VAL procedure.
ONF procedure (Figure 9(b)): given a training set TR, this procedure is applied to select the optimal number of features based on a ranking method. A resampling procedure is iterated K times, each time producing a (TR
k
, TS
k
) split of TR. A feature ranking method is applied to TR
k
producing a ranked list RF
k
; a family (M
ki
, F
ki
) of models M
ki
is produced, one for each increasing F
ki
feature subsets. The M
ki
models are evaluated on the TS
k
test data, computing test errors TE
ki
, and the average error curve  is obtained. An exponential fit procedure is applied, and the n* value leading to saturation in terms of the exponential curve is returned as the ONF result.
is obtained. An exponential fit procedure is applied, and the n* value leading to saturation in terms of the exponential curve is returned as the ONF result.
VAL procedure (Figure 9(c)): the OFS-M procedure is validated over B replicated experiments (runs) using a resampling scheme. The model with n* features is operated on the test set, in order to minimize risk of data overfitting, obtaining a TEberror. The procedure returns the expected test error  and a resulting feature ranking score RF.
and a resulting feature ranking score RF.
The first step is to build the (SVM) model through the OFS-M procedure on the whole dataset. As a resampling scheme for the ONF procedure, for compatibility with class cardinalities in the microarray data sets, we use a three-fold cross-validation and we obtain the optimal feature set for the data set, as in Figure 5(a). The feature ranking criteria considered are E-RFE, RFE, SQRT-RFE, Correlation Coefficients (CC) and T-score (TT): for proper comparisons, the same datasets (from resampling as well as from the training/test splits) are used for all criteria. For the model validation, we set up B = 50 experiments according to the following guidelines:
-
the resampling scheme used in the VAL procedure consists in splitting the dataset into training and test set with proportion 3/4-1/4; class priors are preserved within the split.
-
the resampling procedure used in ONF is a three-fold cross-validation; class priors are preserved within the folds.
-
the curve representing the cross-validation error versus the number of mostly relevant features given in the previous step is fitted by an exponential map
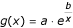
(a, b estimated by least-squares);
-
the optimal number n* of mostly relevant features for the running experiment is chosen as the point where the error difference with respect to the next point is less than 1/1000 of the cross-validation error range (i.e. the difference between the maximum and the minimum cross-validation error); two examples of this fitting procedure are reported in Figures 5(b) and 5(a).
The total number of extractions (multiplicity) of the n selected features from the optimal feature sets over all the B experiments of the VAL procedure additionally provides a measure of relative importance for the selected features.
Finally, a randomization procedure was used to detect design problems. First we built 50 new data sets starting from the colon cancer dataset by randomizing the labels via permutation and then we applied B = 20 times the VAL procedure on each of those no-information data sets. Since a statistical analysis (t-test) revealed that fewer randomizations were sufficient to reach a significant result, a procedure involving only 25 new data sets (built as in the colon cancer case), each undergoing B = 10 VAL runs, was set up for the lymphoma data set. No randomization procedure was carried out for the tumor vs. metastases data set due the heavy workload of the involved computation.
E-RFE
The Recursive Feature Elimination (RFE) is a well-known feature selection method for support vector machines (SVM), firstly introduced in [6]. In brief, a SVM realizes a classification function  , where the coefficients α = (α
i
) and b are obtained by training over a set of examples S = {(x
i
, y
i
}i=1,...,N, x
i
∈
, where the coefficients α = (α
i
) and b are obtained by training over a set of examples S = {(x
i
, y
i
}i=1,...,N, x
i
∈  , y
i
∈ {-1, 1} and K(·, ·) is the chosen kernel. In the linear case, the SVM expansion defines the hyperplane f(x) = <w, x> + b, with
, y
i
∈ {-1, 1} and K(·, ·) is the chosen kernel. In the linear case, the SVM expansion defines the hyperplane f(x) = <w, x> + b, with  . The idea is to define the importance of a feature for a SVM in terms of its contribution to a cost function J(α). At each step of the RFE procedure, a SVM is trained on the given data set, J is computed and the feature less contributing to J is discarded. In the case of linear SVM, the variation due to the elimination of the i-th feature is
. The idea is to define the importance of a feature for a SVM in terms of its contribution to a cost function J(α). At each step of the RFE procedure, a SVM is trained on the given data set, J is computed and the feature less contributing to J is discarded. In the case of linear SVM, the variation due to the elimination of the i-th feature is  ; in the non linear case,
; in the non linear case,  , where Z
i,j
= y
i
y
j
K (x
i
, x
j
). The heavy computational cost of RFE is a function of the number of variables, because a SVM must be trained each time a variable is removed. The removal of chunks of variables at every loop represents a feasible approach, and it was suggested in [6]. However, at the first loops of the RFE algorithm, many weights are generally similar and concentrated nearby zero, as shown in Figure 3(a). In the standard RFE algorithm we would eliminate just one of the many features corresponding to a minimum weight, while it would be convenient to remove all of them at once. Another possible choice is to remove
, where Z
i,j
= y
i
y
j
K (x
i
, x
j
). The heavy computational cost of RFE is a function of the number of variables, because a SVM must be trained each time a variable is removed. The removal of chunks of variables at every loop represents a feasible approach, and it was suggested in [6]. However, at the first loops of the RFE algorithm, many weights are generally similar and concentrated nearby zero, as shown in Figure 3(a). In the standard RFE algorithm we would eliminate just one of the many features corresponding to a minimum weight, while it would be convenient to remove all of them at once. Another possible choice is to remove  ; features at each step, where R is the set of the remaining features, thus obtaining the SQRT-RFE procedure. We developed an ad hoc strategy for an elimination process based on the structure of the weight distribution. This strategy was first described in [28]. We introduce an entropy function H as a measure of the weight distribution. To compute the entropy, we split the range of the weights, normalized in the unit interval, into n
int
intervals (with n
int
=
; features at each step, where R is the set of the remaining features, thus obtaining the SQRT-RFE procedure. We developed an ad hoc strategy for an elimination process based on the structure of the weight distribution. This strategy was first described in [28]. We introduce an entropy function H as a measure of the weight distribution. To compute the entropy, we split the range of the weights, normalized in the unit interval, into n
int
intervals (with n
int
=  ), and we compute for each interval the relative frequencies
), and we compute for each interval the relative frequencies

Entropy is then defined as the following function:

The following inequality immediately descends from the definition of entropy:
-
0
≤ H ≤ log2 n int .
The two bounds corresponds to the situations:
-
H = 0: all the weights lie in one interval;
-
H = log2n int : all the intervals contain the same number of weights.
The new entropy-based RFE (E-RFE) algorithm eliminates chunks of genes at every loop, with two different procedures applied for lower or higher values of H. A scheme is detailed in Figure 10. The distinction is needed to remove many genes that have a similar (low) weight while preserving the residual distribution structure, and also allowing for differences between microarray classification problems. Let {pw
i
}i∈Rbe the projected weights, i.e. the weights linearly projected in the interval [0,1] ; let H be their entropy and H
t
a threshold to discriminate feature importance. We set  to equally split the entropy values range. When H >H
t
the weights are not concentrated: nevertheless, in some cases, many of them have approximately the same low value, as shown in Figure 3(b).
to equally split the entropy values range. When H >H
t
the weights are not concentrated: nevertheless, in some cases, many of them have approximately the same low value, as shown in Figure 3(b).
To take care of the situation where many weights are close to 0, it is necessary to introduce a further discriminating measure. Let M be the mean of the projected weights and M t a suitable threshold for such a measure. This threshold must be chosen to decide which projected weights should be eliminated: in fact, the situations where M ≤ M t are precisely those when many features should be discarded. A meaningful value for the considered datasets is M t = 0.2.
When H >H
t
and M >M
t
(as in Figure 3(c)), the features whose weight lies in the interval  are discarded. In the remaining cases (H >H
t
and M ≤ M
t
, as in Figure 3(b), or H ≤ H
t
, Figure 3(a)), we cautiously discard the features whose weight is in the leftmost quantile through a bisection procedure. The stopping condition is that no more than half of the features with weights in
are discarded. In the remaining cases (H >H
t
and M ≤ M
t
, as in Figure 3(b), or H ≤ H
t
, Figure 3(a)), we cautiously discard the features whose weight is in the leftmost quantile through a bisection procedure. The stopping condition is that no more than half of the features with weights in  should be discarded. We take a conservative approach by reverting to one-step RFE when the number of variables has been reduced below a threshold value R
t
, which has to be chosen as a suitable compromise between the computational cost and the estimated size of supposed optimal features subset. For the three microarray data sets R
t
= 100 was used. As a further caution, the classification methods were compared at a finer resolution for smaller subsets of genes: every single step at 1–15 genes, every 5 at 15–50, every 10 at 50–200, every 100 at 200–1000. The extensive comparisons among methods with the complete validation scheme were run on a Open-Mosix cluster of 38 processing units (1 GHz Pentium).
should be discarded. We take a conservative approach by reverting to one-step RFE when the number of variables has been reduced below a threshold value R
t
, which has to be chosen as a suitable compromise between the computational cost and the estimated size of supposed optimal features subset. For the three microarray data sets R
t
= 100 was used. As a further caution, the classification methods were compared at a finer resolution for smaller subsets of genes: every single step at 1–15 genes, every 5 at 15–50, every 10 at 50–200, every 100 at 200–1000. The extensive comparisons among methods with the complete validation scheme were run on a Open-Mosix cluster of 38 processing units (1 GHz Pentium).
References
Weston J, Mukherjee S, Chapelle O, Pontil M, Poggio T, Vapnik V: Feature selection for SVMs. In Advances in Neural Information Processing Systems (NIPS) 13, 2000 (Edited by: TK Leen, TG Dietterich, V Tresp). MIT Press 2001, 668–674.
Li Y, Campbell C, Tipping M: Bayesian automatic relevance determination algorithms for classifying gene expression data. Bioinformatics 2002, 18: 1332–1339. 10.1093/bioinformatics/18.10.1332
Zhang X, Wong W: Recursive sample classification and gene selection based on SVM: method and software description. Technical report, Department of Biostatistics, Harvard School of Public Health 2001.
Xiong M, Fang X, Zhao J: Biomarker identification by feature wrappers. Genome Research 2001, 11: 1878–1887.
Nguyen DV, Rocke DM: Tumor classification by partial least squares using microarray gene expression data. Bioinformatics 2002, 18: 39–50. 10.1093/bioinformatics/18.1.39
Guyon I, Weston J, Barnhill S, Vapnik V: Gene selection for cancer classification using support vector machines. Machine Learning 2002, 46: 389–422. 10.1023/A:1012487302797
Golub T, Mukherjee S, Tamayo P, Slonim D, Verri A, Poggio T, Mesirov J: Support vector machine classification of microarray data. Technical Report 182/AI Memo CBCL Paper 1676.
Furey T, Cristianini N, Duffy N, Bednarski D, Schummer M, Haussler D: Support vector machine classification and validation of cancer tissue samples using microarray expression data. Bioinformatics 2000, 16: 906–914. 10.1093/bioinformatics/16.10.906
Slonim D: From patterns to pathways: gene expression data analysis comes of age. Nature genetics supplement 2002, 32: 502–507. 10.1038/ng1033
Ramaswamy S, Ross K, Lander E, Golub T: A molecular signature of metastasis in primary solid tumors. Nature Genetics 2003, 33: 1–6. 10.1038/ng1060
Kari L, Loboda A, Nebozhyn M, Rook A, Vonderheid E, Nichols C, Virok D, Chang C, Horng WH, Johnston J, et al.: Classification and prediction of survival in patients with the leukemic phase of Cutaneous T Cell Lymphoma. J Exp Med 2003, 1477–1488. 10.1084/jem.20021726
Nutt CL, Mani D, Betensky RA, Tamayo P, Cairncross JG, Ladd C, Ute Pohl CH, McLaughlin ME, Batchelor TT, Black PM, et al.: Gene expression-based classification of malignant gliomas correlates better with survival than histological classification. Cancer Res 2003, 63: 1602–1607.
Ramaswamy S, Tamayo P, Rifkin R, Mukherjee S, Yeang C, Angelo M, Ladd C, Reich M, Latulippe E, Mesirov J, et al.: Multiclass cancer diagnosis using tumor gene expression signatures. Proc Natl Acad Sci 2001, 98: 15149–15154. 10.1073/pnas.211566398
Weston J, Elisseeff A, Tipping M, Schölkopf B: Use of the zero norm with linear models and kernel methods. Journal of Machine Learning Research 2002, 3: 1439–1461. 10.1162/153244303322753751
Rakotomamonjy : Variable selection using SVM-based criteria. Journal of Machine Learning Research 2002, 1357–1370.
Ambroise C, McLachlan G: Selection bias in gene extraction on the basis of microarray gene-expression data. Proc Natl Acad Sci USA 2002, 99: 6562–6566. 10.1073/pnas.102102699
Simon R, Radmacher M, Dobbin K, McShane L: Pitfalls in the use of DNA microarray data for diagnostic and prognostic classification. J Natl Cancer Inst 2003, 95: 14–18. 10.1093/jnci/95.1.14
Spang R, Blanchette C, Zuzan H, Marks J, Nevins J, West M: Prediction and uncertainty in the analysis of gene expression profiles. In Silico Biology 2002, 2: 0033. [http://www.bioinfo.de/isb/2002/02/0033/]
Hastie T, Tibshirani R, Friedman J: The Elements of Statistical Learning. New York: Springer-Verlag 2001.
Weston J, Pérez-Cruz F, Bousquet O, Chapelle O, Elisseeff A, Schölkopf B: Feature Selection and Transduction for Prediction of Molecular Bioactivity for Drug Design. Bioinformatics 2002, 1: 1–8.
Bø T, Jonassen I: New feature subset selection procedures for classification of expression profiles. Genome Biology 2002, 3: research0017.1–0017.11. 10.1186/gb-2002-3-4-research0017
Li W, Yang Y: Zipf's law in importance of genes for cancer classification using microarray data. Journal of Theoretical Biology 2002, 219: 539–551. 10.1006/jtbi.2002.3145
Alon U, Barkai N, Notterman D, Gish K, Ybarra S, Mack D, Levine A: Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc Natl Acad Sci USA 1999, 96: 6745–6750. 10.1073/pnas.96.12.6745
Alizadeh A, Eisen M, Davis E, Ma C, Lossos I, Rosenwald A, Boldrick J, Sabet H, Tran T, Yu X, et al.: Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature 2000, 403: 503–511. 10.1038/35000501
Furusawa C, Kaneko K: Zipf's law in gene expression. Phys Rev Lett 2003, 90: 088102. 10.1103/PhysRevLett.90.088102
Xing EP: Feature selection in microarray analysis. In Understanding and using Microarray Analysis Techniques: a Practical Guide (Edited by: D Berrar, W Dubitzky, M Granzow). Kluwer Academic Publishers 2003.
Raychaudhuri S, Sutphin P, Chang J, Altman R: Basic microarray analysis: grouping and feature reduction. Trends in Biotechnology 2001, 19: 189–193. 10.1016/S0167-7799(01)01599-2
Furlanello C, Serafini M, Merler S, Jurman G: An accelerated procedure for recursive feature ranking on microarray data. Neural Networks 2003, 16: 641–648. 10.1016/S0893-6080(03)00103-5
Acknowledgments
MS is supported by the FUPAT 'WebFAQ grant'. BJ is supported by the FUPAT post-graduate project 'Algorithms and software environments for microarray gene expression experiments'. We thank T. Poggio, G. Anzellotti and B. Caprile for helpful discussions and comments, and E. Manduchi and J. Reid for reading earlier versions of the manuscript. We are grateful to R. Flor and A. Soraruf for assistance in developing and administrating the computing facility.
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
CF devised the study and drafted the manuscript. MS designed the study methodology and performed the data analysis. SM devised the machine learning methods and contributed to the validation methodology. GJ organized the experimental results and contributed to the study methodology. All authors equally contributed to, read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
About this article
Cite this article
Furlanello, C., Serafini, M., Merler, S. et al. Entropy-based gene ranking without selection bias for the predictive classification of microarray data. BMC Bioinformatics 4, 54 (2003). https://doi.org/10.1186/1471-2105-4-54
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2105-4-54