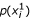- Methodology article
- Open access
- Published:
Feature selection for splice site prediction: A new method using EDA-based feature ranking
BMC Bioinformatics volume 5, Article number: 64 (2004)
Abstract
Background
The identification of relevant biological features in large and complex datasets is an important step towards gaining insight in the processes underlying the data. Other advantages of feature selection include the ability of the classification system to attain good or even better solutions using a restricted subset of features, and a faster classification. Thus, robust methods for fast feature selection are of key importance in extracting knowledge from complex biological data.
Results
In this paper we present a novel method for feature subset selection applied to splice site prediction, based on estimation of distribution algorithms, a more general framework of genetic algorithms. From the estimated distribution of the algorithm, a feature ranking is derived. Afterwards this ranking is used to iteratively discard features. We apply this technique to the problem of splice site prediction, and show how it can be used to gain insight into the underlying biological process of splicing.
Conclusion
We show that this technique proves to be more robust than the traditional use of estimation of distribution algorithms for feature selection: instead of returning a single best subset of features (as they normally do) this method provides a dynamical view of the feature selection process, like the traditional sequential wrapper methods. However, the method is faster than the traditional techniques, and scales better to datasets described by a large number of features.
Background
The DNA sequences of most genes code for messenger RNA (mRNA) that is, in turn, encoding proteins. Whereas in prokaryotes the mRNA is a mere copy of a fragment of the DNA, in eukaryotes the RNA copy of DNA (primary transcript or pre-mRNA) contains non-coding segments (introns) which should be precisely spliced out to produce the mRNA. The border sides of such introns are referred to as splice sites. The splice site in the upstream part of the intron is called the donor site, the downstream site is termed the acceptor site.
During the last years, large datasets containing the sequences of several eukaryotic genomes became available. Such datasets allow us to use supervised machine learning techniques to automate the process of splice site prediction. The identification of these sites constitutes the major subtask in gene prediction and is of key importance in determining the exact structure of genes in genomic sequences. An extensive overview of splice site recognition can be found in [1], while a more general overview and a comparison of gene and splice site prediction is discussed in [2] and [3]. More recent work on splice site prediction for the human genome include methods base on maximum entropy modelling [4] and support vector machines [5].
To increase the probability of including relevant information, machine learning methods are typically provided with many features describing the data. In most cases however, not all of these features will be relevant to the classification task, often decreasing the classification performance of the learning algorithm. Therefore, there is a need to incorporate techniques that search for a "minimal" set of features with "best" classification performance. These techniques are often referred to as feature subset selection (FSS) or dimensionality reduction techniques.
Genetic algorithms (GA) have been applied successfully to the identification of relevant feature subsets in small scale (less than 100 features) domains [6–8]. During the last decade estimation of distribution algorithms (EDA) emerged as a new form of evolutionary computation [9–12]. In previous work [13], the use of EDAs for selecting a constrained subset of features was shown to yield a considerable speed-up in time with respect to the traditional wrapper methods for feature selection.
In this paper we elaborate further on these ideas and demonstrate how an EDA can be used to provide a dynamical view of the feature selection process. This offers new possibilities for identifying how much and which features are minimally needed before classification performance drastically goes down, and provides more insight into the biological problem of splicing. This is demonstrated by the detection of a new, biologically motivated feature, that we refer to as AG-scanning.
Methods
Splice site datasets
We constructed a dataset of splice sites for Arabidopsis thaliana. This was done as follows. We obtained mRNAs from the public EMBL database and aligned them to the BAC sequences that were used during the assembly of the Arabidopsis chromosomes. Afterwards the dataset was cleaned, by removing redundant genes, which resulted in a dataset of 1495 genes. From these genes, only the introns with canonical splice sites (GT for donor and AG for acceptor) were retained and used as positive instances. Negative instances were defined as GT or AG dinucleotides in the interval between 300 nucleotides upstream of the donor of the first intron and 300 nucleotides downstream of the acceptor of the last intron in that gene and that are not annotated as a splice site. More details on the construction of the datasets can be found in [13] and [14].
Feature extraction
Splice site prediction can be divided into two subtasks: prediction of donor sites and prediction of acceptor sites. Each of these subtasks can be formally stated as a two-class classification task: {donor site, non-donor site} and {acceptor site, non-acceptor site}. The features describing the positive and negative instances were extracted from a local context around the splice site. In our experiments we used a window of 50 nucleotide positions to the left (upstream of the splice site) and 50 positions to the right (downstream of the splice site). Features were then extracted from this local context, resulting in three datasets with growing complexity.
Dataset 1 is the most simple dataset, containing only position-dependent nucleotide information. This results in a dataset described by 100 (50 to the left, 50 to the right) features. These features were converted into a binary format using a sparse vector encoding, yielding 400 binary features.
Dataset 2 adds to these position-dependent features also a number of position-independent features, representing the occurrence of trimers (words of length three) in the flanking sequence. An example of such a feature is the occurrence of the word "ATC" in the upstream part of the splice site. This yields another 128 binary features, summing up to 528 binary features for the second dataset version.
Dataset 3 adds another layer of position-dependent information: the position-dependent dimers. This results in an additional set of 1568 features (49 × 16 × 2), summing up to 2096 features for the third dataset. It should be noted that adding position-dependent dimers already captures dependencies between adjacent nucleotides at the feature level. This allows us to still use linear classification models, yet take into account nucleotide dependencies. Another advantage of incorporating the dependencies at the feature level, is the ease to visualise and interpret feature dependencies using feature selection, as will be shown further. Note that these features only model dependencies between pairs of adjacent bases, but not between non-neighbouring bases.
For each of the three datasets, different training and test sets were compiled. This was done as follows. Each dataset was split into a train and a test set, each containing 3000 positive and 18,000 negative instances. This class imbalance was chosen, because it is a more realistic view of real sequences, where the number of pseudo sites also outnumbers the amount of real sites. This process of splitting was replicated five times, resulting in five pairs of training and test sets, allowing us to perform a 10-fold cross-validation (5 × 2). The results described further are all averaged over these 10 folds.
Estimation of Distribution Algorithms
Standard GAs have been criticized in the literature for a number of aspects: the large number of parameters that have to be tuned, the difficult prediction of the movements of the populations in the search space and the fact that there is no mechanism for capturing the relations among the variables of the problem [10, 11]. EDAs try to overcome these difficulties by providing a more statistical analysis of the selected individuals, thereby explicitly modelling the relationships among the variables. Instead of using the traditional crossover and mutation operators as in GAs, the further exploration of the search space is guided by the probabilistic modelling of promising solutions. The main scheme of the EDA approach is shown in Figure 1. In a first step, the initial population is generated. From this population a subset of promising individuals is selected. This is done by calculating an evaluation measure (often called the fitness) for each individual and afterwards selecting a number of individuals (mostly the best half of the population). In the case of feature selection, each individual is a binary feature vector, each bit representing the presence (1) or absence (0) of a particular feature. The evaluation can then be calculated as the classification performance of a machine learning method when using only the features having a 1 in the binary vector. This will be discussed in more detail in the following sections.
An iterative procedure repeating steps 2, 3 and 4 (see Figure 1) is then carried out until a termination criterion is met. Such a criterion can either be quantitative, like a fixed number of iterations, or qualitative, like a lower limit on the evaluation measure that has to be reached. In each iteration, a number of individuals is selected from the population and from these a probability distribution of the encoded variables is estimated. Afterwards, the estimated probability distribution is used to generate the next population. This is done by sampling the probability distribution, i.e. generating individuals according to this distribution.
The actual estimation of the underlying probability distribution represents the core of the EDA paradigm, and can be considered an optimization problem on its own. Depending on the domain (discrete or continuous), different estimation algorithms with varying complexity (modelling univariate, bivariate or multivariate dependencies) were designed [10]. In the most complex case of multivariate dependencies, Bayesian Networks are frequently used. A greedy search algorithm is then used to find a suitable (and often constrained) network that is likely to generate the selected individuals.
The use of EDAs for feature subset selection was pioneered in [12] and the use of EDAs for FSS in large scale domains was reported to yield good results [10, 13].
The Univariate Marginal Distribution Algorithm
As an example of an EDA, we will consider here the Univariate Marginal Distribution Algorithm (UMDA, [15]). The UMDA is a simple estimation algorithm, based on the assumption that all variables are independent. For each iteration l the probability model p
l
(x) that is induced from a selected number of individuals (step 3 in Figure 1) is estimated as 
Here each p
l
(x
i
) (the relative frequency) is estimated from the selected set (Se) of individuals of the previous generation  . A new individual is then generated by sampling a value from the distribution p
l
(x
i
) for each variable x
i
.
. A new individual is then generated by sampling a value from the distribution p
l
(x
i
) for each variable x
i
.
It has to be pointed out that the EDA-UMDA approach is very similar to the compact GA [16] or to a GA with uniform crossover. Although these algorithms assume independence between variables, it has been shown that they are fast and robust for feature selection [17, 10].
Classification methods
Two classification methods were used in our experiments: the Naive Bayes classifier and the Support Vector Machine. These methods are known to perform well in high dimensional spaces. They are supervised classification methods that induce a decision function from the instances in a training set that can then be used to classify a new instance. The Support Vector Machine (SVM, [18, 19]) is a data-driven method for solving two-class classification tasks. In our experiments we used a linear SVM. The Naive Bayes method (NBM, [20]) follows the Bayes optimal decision rule, combining it with the assumption that the probability of the features given the class is the product of the probabilities of the individual features. It is known that the NBM can achieve considerably better results when FSS is applied [21], yet also the SVM can benefit from feature selection, although it already performs an implicit feature weighting based on the maximisation of the margin [22].
Feature subset selection methods
Techniques for FSS are traditionally divided into two classes: filter approaches and wrapper approaches [23]. In the case of filter methods a feature relevance score is calculated, and low-scoring features are removed, providing a mechanism that is independent of the classification method to be used. In the wrapper approach various subsets of features are generated and evaluated, typically using greedy (iterative forward or backward methods) or heuristic search methods (GA, EDA). This approach is used with a specific classification algorithm, as the outcome of the evaluation is used during the search. Additionally one can distinguish a third class of FSS methods where the feature selection mechanism is built into the model [22].
In general, the use of wrapper methods is preferred, as this approach is better able to deal with datasets where many correlations between features exist. On the other hand, wrapper techniques are computationally very demanding, because for each feature subset a classification model has to be trained and evaluated. The technique we describe here is an EDA-based heuristic wrapper approach, that scales better to larger feature sets than the traditional wrapper methods, as will be shown further in this paper. Traditionally, FSS techniques based on GAs or EDAs use the single best subset of features as the result of the search. Here we elaborate further on these ideas and show how the EDA can be used to derive a more dynamic view of the feature selection process.
Feature ranking using EDA-UMDA
The most common usage of GAs/EDAs in feature selection is to search for a subset of features, representing the "best" solution, i.e. one that maximises the classification performance of the classification model on the training (using cross-validation) or holdout set. This is done by evolving a population, where at the end of the iterative process the best scoring individual is regarded as "the solution".
It should be noted that such a single best subset of features provides a rather static view of the whole elimination process. When using FSS to gain more insight in the underlying processes, the human expert does not know the context of the specific subset. Questions about how much and which features can still be eliminated before the classification performance drastically drops down remain unanswered using a static analysis, although these would provide interesting information.
Feature ranking is a first step towards a dynamical analysis of the feature elimination process. The result of a feature ranking is an ordering of the features, sorted from the least relevant to the most relevant. Starting from the full/empty feature set, features can then be removed/added and the classification performance for each subset can be calculated, providing a dynamic view.
A solution to the traditional, static approach lies in the fact that the outcome of an EDA should not be restricted to the single best individual from the population, yet the distribution estimated from the population can be used as a whole to yield better generality than a single solution. To derive a feature ranking from a probability distribution, some sort of importance or relevance score for each feature needs to be calculated. Evidently, a feature i having a higher value for  can be considered more important than a feature j with a lower value for
can be considered more important than a feature j with a lower value for  . The generalized probabilities
. The generalized probabilities  can thus be considered as feature relevance scores, and a list of features sorted by these probabilities returns a feature ranking. The general algorithm to calculate such a ranking (EDA-R) consists of the steps presented below.
can thus be considered as feature relevance scores, and a list of features sorted by these probabilities returns a feature ranking. The general algorithm to calculate such a ranking (EDA-R) consists of the steps presented below.
Algorithm EDA-R
-
1.
Select S individuals from the final population D final
-
2.
Construct the probability model P from
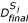 , j = 1... S, using an EDA (UMDA, BMDA, BOA/EBNA)
, j = 1... S, using an EDA (UMDA, BMDA, BOA/EBNA) -
3.
For each variable (feature) X i , calculate the probability
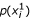
-
4.
Sort the features X1 ,..., X n by their probabilities
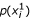
-
5.
List the array of sorted features
The most important step in this algorithm is the extraction of the probabilities

from the model. For models with univariate dependencies like the UMDA, the extraction of these probabilities is trivial, as they can be directly inferred from the model. For higher order EDAs the probabilities  need to be calculated in a forward manner, as they may involve conditional probabilities.
need to be calculated in a forward manner, as they may involve conditional probabilities.
The feature ranking can then be used afterwards to iteratively discard features. It should be noted that this ranking is specific to the classification model that was used during the search. The number of classification models that have to be trained can be easily calculated. For an EDA with a population size P, running for I iterations, the number of model evaluations is P(I+1).
Other techniques
We compared EDA-based feature ranking to two other selection strategies. The first of these is a traditional sequential wrapper approach, known as sequential backward elimination (SBE). SBE starts with the full feature set and iteratively discards features. At iteration l the feature set consists of n
l
features and n
l
models have to be trained, leaving out each feature once in each model. At iteration l+1 the feature set for the model with the best predictive performance is then chosen as the new feature subset. For a feature set of size n the number of classification models to be trained and evaluated when a complete view of the selection process is required is  . One could also use a sequential forward selection procedure, but in general correlated features are better discovered using a backward approach.
. One could also use a sequential forward selection procedure, but in general correlated features are better discovered using a backward approach.
The second method is an advanced filter method, described by Koller and Sahami [24], further referred to as KS. This filter method is based on Markov blankets, being able to discover feature interactions, a property that does not apply for all filter methods. During the first step a correlation matrix is calculated, requiring O(n2(m + log n)) operations, m being the number of instances in the training set. During the second step, the actual feature selection is done. The parameter k in the algorithm represents a small, fixed number of conditioning features, typically set to 0,1 or 2. For this parameter in the algorithm we used the value 1 in all our experiments, requiring an additional O(2n2m) operations for a complete view of the selection process.
Selection criterion
The determination of the classification performance for a specific subset of features greatly influences the feature selection mechanism. In our experiments we used the F-measure as a measure of classification performance, because it is better able to deal with imbalanced datasets than the traditional accuracy measure [25].

TP and TN represent the number of true positives and true negatives, FP and FN the number of false positives/negatives.
Implementation
The methods for feature selection were all implemented in C++, using the SVMlightimplementation for SVMs [26]. Both SBE and EDA are suitable candidates for parallellization, providing a linear gain in speed of the selection process. For parallellization, we made use of the MPI libraries, available at [27]. All experiments ran on a cluster of 5 dual-processor (1.2 Ghz) Linux machines running RedHat Linux 7.2. The source code is available from the authors upon request.
Results and discussion
All results were averaged using 10-fold cross-validation. Using the EDA-approach, the internal evaluation of a feature subset was calculated on a 5-fold cross-validation of the training set. For the different datasets, the C-parameter of the SVM was tuned on the full feature set: C = 0.05 for datasets 1 and 2, C = 0.005 for dataset 3. These values were determined experimentally using a cross-validation procedure. For the EDA-approach, the population size was tuned to 500 individuals, and the number of iterations was set to 20. At each iteration in the EDA, the probability model was estimated using the best half of the distribution. For the largest dataset (2096 features) the SBE approach turned out to be infeasible, due to the large number of models that needs to be evaluated.
Figure 2 compares the results for the three feature selection methods on the three datasets when NBM is used as classifier. At the x-axis the number of features eliminated so far is represented, while the y-axis measures the classification performance (F-measure). Several conclusions can be drawn from these results. A general observation is that many features can be eliminated before the classification performance drastically goes down. This illustrates the fact that the datasets contain many irrelevant or correlated features, as removing these features does not harm the classification performance. Furthermore it can be noted that better results can be obtained using the more complex datasets (adding position-independent trimers and position-dependent dimers), proving the usefulness of including such kind of features. A second observation is that the wrapper methods (EDA-R and SBE) consistently perform better than the filter method (KS), and that EDA-R achieves better results than SBE.
Comparison of feature selection techniques. For each of the three datasets, the different feature selection techniques are compared with NBM used as a classifier. The x-axis denotes the number of features that has been eliminated so far, while the y-axis shows the classification performance (F-measure).
In addition to the comparison of classification performance, an important aspect to consider is the running time. In this respect KS, being a filter approach, is the fastest algorithm for the datasets we used. To compare EDA-R and SBE, the formulas given earlier can be used to calculate the number of model evaluations that is needed. For the datasets containing 528 features, an SBE approach eliminating one feature at the time requires 139,656 model evaluations, while the EDA-R method needs only 10,500 model evaluations, a reduction by approximately one order of magnitude. For the largest dataset (2096 features) the EDA-R method achieves good results, and needed only 10,500 model evaluations, while the SBE approach would need 2,197,656 model evaluations, a reduction by more than two orders of magnitude.
Clearly, the EDA-R method scales better to datasets with many features. Another advantage of EDA-R is the fact that the number of model evaluations needed is not directly dependent on the number of features. It is only indirectly dependent through the classification algorithm that is used in the EDA-process.
As both NBM and SVM scale well in the number of features used, the use of EDA-R with these models provides advantages over SBE and KS, both being quadratic in the number of features. As a consequence, the use of SBE and KS will turn out to be infeasible as the number of features gets larger, while the use of EDA-R will still produce results.
As we already mentioned in the introduction, a key advantage of applying FSS methods is the extraction of knowledge from complex datasets. Using the different datasets mentioned earlier, we now discuss the advantages of the EDA-R approach to gain more insight into the classification of acceptor and donor splice sites.
Acceptor prediction
An important advantage of the EDA-R method, compared to the sequential backward wrapper and the filter method, is the fact that the relative frequencies of the features in the final distribution can be used as an importance measure, or feature weight. As a result, several gradations of the importance of features can be distinguished and visualised, which cannot be done using only a feature ranking.
To visualise the results of the EDA-R feature selection method, the feature weights can be color coded using a so-called heat map. On a heat map, the interval [0,1] is mapped to a color gradient changing from blue (0), over green (0.5) to red (1). The results of such a color coding of the features for acceptor prediction are shown in Figure 3. In this figure, the features for dataset 1 (400 features, Figure 3A), dataset 2 (528 features, Figure 3B) and dataset 3 (2096 features, Figure 3C) are shown when EDA-R is combined with the linear SVM. Figure 3A represents the dataset containing only position-dependent nucleotides. For each of the four nucleotides (shown as four rows), each column represents a position in the local context of the acceptor site (the upstream part is shown on the left and the downstream part is shown on the right). Figure 3B shows the features of the second dataset, containing also the position invariant trimers. For each part of the context (upstream, downstream), the trimers are grouped according to their composition: the first four columns represent trimers with a bias to the respective nucleotides A, T, C and G. The last two columns represent the remaining trimers. In Figure 3C, the position-dependent dimers are included, where each row again represents a specific dimer. The color gradients for each of the three datasets clearly reveal some insightful patterns.
Visualization of EDA-R feature weights for acceptor prediction. For each of the three datasets, the color coded feature weights as a result of the EDA-R feature selection in combination with a linear SVM are shown. (A) The simplest dataset (only position dependent nucleotides, 400 binary features). (B) The extended (position dependent nucleotides + position invariant 3-mers, 528 binary features). (C) The most complex dataset (also including position dependent dinucleotides, 2096 binary features).
For example, the bases flanking the acceptor site turn out to be of key importance in distinguishing true sites from pseudo sites. These features represent the consensus around the acceptor site. Also note the importance of the dimer features in the immediate neighbourhood of the splice site, capturing local dependencies.
The existence of a poly-pyrimidine (nucleotides C and T) stretch in the upstream part (about 20 nucleotides) of the acceptor also appears to be a strong feature. Further, it can be noticed that in this pyrimidine stretch, the nucleotide T is of higher importance than the C. This fits with the current knowledge on spliceosomal splicing first documented in yeast and mammals [28]. Even if T-rich sequences are reported to be spread all over the introns in plants [29], our observation indicates that poly-pyrimidine tracts do play a specific role in acceptor recognition in plants as well. Another feature related to the poly-pyrimidine tract is the importance of TG-dinucleotides upstream of the acceptor (Figure 3C). A position-frequency plot of this dinucleotide is shown in Figure 4, from which we can conclude that the TG is more abundant in true acceptors.
The fact that the acceptor site is a boundary between a non-coding region (intron) and a coding region (exon) is also reflected in the features that are selected. A three-base periodicity in the features, especially for the bases G, T and C, can be observed downstream of the acceptor site, as expected for coding regions. Furthermore, some position invariant features are of great importance, shown by the fact that the periodic pattern becomes less apparent if position invariant features are considered. This illustrates the importance of the position invariant features in capturing codon bias.
AG-scanning feature
In the largest data set (Figure 3C), the dinucleotide "AG" appears as a very strong feature in the region up to about 25 positions upstream of the acceptor site. Naturally, in the local context of true acceptors, this dinucleotide should not appear in this region, because it is known that the acceptor site is usually the first "AG" following the branch point [30]. Selection against AG dinucleotides in the upstream part of true acceptors is shown in Figure 5, where the positional frequencies of the dinucleotide AG is compared for the true and pseudo acceptors. The prominence of this feature in this region points to the fact that in Arabidopsis the branch point should be at least about 25 positions upstream of the acceptor site, which fits with the ± 30 nt distance of branch points to acceptors, previously reported for plants [29].
Donor prediction
A similar analysis was done for donor sites. The results for the most complex dataset (2096 features) are shown in Figure 6. Analogous to acceptor prediction, the strongest features are the ones that represent the consensus sequence around the donor site, both for the position dependent nucleotides and dinucleotides. Also in this case, some of the position invariant features are highly relevant for classification, for example the T-rich trimers TTA and TTT in the downstream part of the context, capturing the T-richness of introns in Arabidopsis.
Visualization of EDA-R feature weights for donor prediction. For the most complex of the three datasets (2096 binary features), the color coded feature weights, resulting from the combination of EDA-R with a linear SVM, are shown. The interpretation is similar to Figure 3.
Another pattern that can be clearly observed is the importance of G immediately downstream of the donor site. A position-frequency plot of the G-percentage in the downstream part of the donor site is shown in Figure 7. From this figure we can learn that the nucleotide G is significantly under-represented in the case of real donor sites, compared to pseudo sites, except at position +3, where a G is over-represented as part of the consensus sequence.
G percentage downstream of the donor site. For both real and pseudo donor sites, the percentage of G nucleotides is shown as a function of the position downstream of the site. The closer to the donor, the less G is tolerated. The only exception occurs at position +3, where a G is clearly over-represented, as part of the donor consensus sequence.
Conclusions
The results discussed in this paper show that feature subset selection using EDA-based ranking provides a robust framework for feature selection in splice site prediction. We presented a method that is easy to implement, can be easily parallellized, and is scalable to larger feature sets. This was obtained at no expense of efficiency. The method can be used for any other optimisation problem where the feature set is sufficiently large, like gene selection in microarray datasets.
An important advantage of our method (EDA-R) is the derivation of feature weights, which is shown to be useful to extract knowledge from complex data. The most prominent example of this was the detection of a new, biologically motivated feature for acceptor prediction, which we termed AG-scanning. Because the knowledge on splicing mechanisms in plants is still limited [29], new findings such as discussed here could both lead to advances in gene prediction and to biologically relevant insights in the mechanisms behind transcription.
Future research on splice site prediction will focus on larger feature sets, including additional information such as structural information to achieve better results. Other future directions we would like to explore are the combination of EDAs with other classification systems, and the development of more complex features that capture other nucleotide dependencies at the feature level.
References
Sonnenburg S: New Methods for Splice Site recognition. Diploma thesis, Humbold-Universität zu Berlin 2002.
Mathé C, Sagot MF, Schiex T, Rouzé P: Current methods of gene prediction, their strengths and weaknesses. Nucleic Acids Res 2002, 30: 4103–4117. 10.1093/nar/gkf543
Zhang MQ: Computational prediction of eukaryotic protein-coding genes. Nat Rev Genet 2002, 3: 698–709. 10.1038/nrg890
Yeo G, Burge CB: Maximum entropy modelling of short sequence motifs with applications to RNA splicing signals. In Proceedings of RECOMB 2003 2003, 322–331.
Zhang X, Heller K, Hefter I, Leslie C, Chasin L: Sequence Information for the Splicing of Human pre-mRNA Identified by Support Vector Machine Classification. Genome Res 2003, 13: 2637–2650. 10.1101/gr.1679003
Kudo M, Sklansky J: Comparison of algorithms that select features for pattern classifiers. Pattern Recogn 2000, 33: 25–41. 10.1016/S0031-3203(99)00041-2
Siedelecky W, Sklansky J: On automatic feature selection. Int J Pattern Recogn 1988, 2: 197–220.
Vafaie H, De Jong K: Robust feature selection algorithms. In Proceedings of the Fifth International Conference on Tools with Artificial Intelligence 1993, 356–363.
Mühlenbein H, Paass G: From recombination of genes to the estimation of distributions. Binary parameters. In Lecture Notes in Computer Science 1411: Parallel Problem Solving from Nature, PPSN IV 1996, 178–187.
Larrañaga P, Lozano JA: Estimation of Distribution Algorithms. A New Tool for Evolutionary Computation Kluwer Academic Publishers 2001.
Larrañaga P, Etxebarria R, Lozano J, Peña J: Combinatorial Optimization by Learning and Simulation of Bayesian Networks. In Proceedings of the 16th Annual Conference on Uncertainty in Artificial Intelligence (UAI-00) Morgan Kaufmann Publishers 2000.
Inza I, Larrañaga P, Etxebarria R, Sierra B: Feature subset selection by Bayesian networks based optimization. Artif Intell 1999, 27: 143–164.
Saeys Y, Degroeve S, Aeyels D, Van de Peer Y, Rouzé P: Fast feature selection using a simple Estimation of Distribution Algorithm: A case study on splice site prediction. Bioinformatics 2003, 19(Suppl 2):II179-II188.
Degroeve S, De Baets B, Van de Peer Y, Rouzé P: Feature subset selection for splice site prediction. Bioinformatics 2002, 18(Suppl 2):S75-S83.
Muhlenbein H: The equation for response to selection and its use for prediction. Evol Comput 1997, 5: 303–346.
Harik GR, Lobo GG, Goldberg DE: The compact genetic algorithm. In Proceedings of the International Conference on Evolutionary Computation 1998, 523–528.
Cantú-Paz E: Feature subset selection by estimation of distribution algorithms. In Proceedings of the Genetic and Evolutionary Computation Conference 2002, 754–761.
Boser B, Guyon I, Vapnik VN: A training algorithm for optimal margin classifiers. In Proceedings of COLT 1992, 144–152.
Vapnik VN: The nature of statistical learning theory. Springer-Verlag 1995.
Duda RO, Hart PE: Pattern Classification and scene analysis New York, NY, Wiley 1973.
Langley P, Sage S: Induction of selective Bayesian classifiers. In Proceedings of the Tenth Conference on Uncertainty in Artificial Intelligence 1994, 399–406.
Guyon I, Weston J, Barnhill S, Vapnik VN: Gene Selection for Cancer Classification using Support Vector Machines. Mach Learn 2002, 46: 389–422. 10.1023/A:1012487302797
Kohavi R, John G: Wrappers for feature subset selection. Artif Intell 1997, 97: 273–324. 10.1016/S0004-3702(97)00043-X
Koller D, Sahami M: Toward optimal feature selection. In Proceedings of the 13th International Conference on Machine Learning 1996, 284–292.
Mladenic D, Grobelnik M: Feature selection on hierarchy of web documents. Decis Support Syst 2003, 35: 45–87. 10.1016/S0167-9236(02)00097-0
Joachims T: Making large-scale support vector machine learning practical. Advances in Kernel Methods: Support Vector Machines (Edited by: Schoelkopf B, Burges C). Cambridge, MA: MIT Press 1998.
MPI libraries[http://www-unix.mcs.anl.gov/mpi/mpich]
Brow DA: Allosteric cascade of spliceosome activation. Annu Rev Genet 2003, 36: 333–360. 10.1146/annurev.genet.36.043002.091635
Lorkovic ZJ, Wieczorek KDA, Lambermon MH, Filipowicz W: Pre-mRNA splicing in higher plants. Trends Plant Sci 2000, 4: 160–167. 10.1016/S1360-1385(00)01595-8
Smith CWJ, Chu TT, Nadal-Ginard B: Scanning and competition between AGs are involved in 3' splice site selection in mammalian introns. Mol Cell Biol 1993, 13: 4939–4952.
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
YS designed the EDA-R procedure and ran the experiments. SD prepared the datasets in this study. DA helped in the mathematical part of the research and PR and YVdP provided the biological interpretation and supervised the research. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
About this article
Cite this article
Saeys, Y., Degroeve, S., Aeyels, D. et al. Feature selection for splice site prediction: A new method using EDA-based feature ranking. BMC Bioinformatics 5, 64 (2004). https://doi.org/10.1186/1471-2105-5-64
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2105-5-64

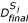 , j = 1... S, using an EDA (UMDA, BMDA, BOA/EBNA)
, j = 1... S, using an EDA (UMDA, BMDA, BOA/EBNA)