- Research article
- Open access
- Published:
An Entropy-based gene selection method for cancer classification using microarray data
BMC Bioinformatics volume 6, Article number: 76 (2005)
Abstract
Background
Accurate diagnosis of cancer subtypes remains a challenging problem. Building classifiers based on gene expression data is a promising approach; yet the selection of non-redundant but relevant genes is difficult.
The selected gene set should be small enough to allow diagnosis even in regular clinical laboratories and ideally identify genes involved in cancer-specific regulatory pathways. Here an entropy-based method is proposed that selects genes related to the different cancer classes while at the same time reducing the redundancy among the genes.
Results
The present study identifies a subset of features by maximizing the relevance and minimizing the redundancy of the selected genes. A merit called normalized mutual information is employed to measure the relevance and the redundancy of the genes. In order to find a more representative subset of features, an iterative procedure is adopted that incorporates an initial clustering followed by data partitioning and the application of the algorithm to each of the partitions. A leave-one-out approach then selects the most commonly selected genes across all the different runs and the gene selection algorithm is applied again to pare down the list of selected genes until a minimal subset is obtained that gives a satisfactory accuracy of classification.
The algorithm was applied to three different data sets and the results obtained were compared to work done by others using the same data sets
Conclusion
This study presents an entropy-based iterative algorithm for selecting genes from microarray data that are able to classify various cancer sub-types with high accuracy. In addition, the feature set obtained is very compact, that is, the redundancy between genes is reduced to a large extent. This implies that classifiers can be built with a smaller subset of genes.
Background
DNA microarrays have become ubiquitous in analyzing the expression profiles of genes in the hope to distinguish between various disease types, such as discriminating between various cancer sub-types. Differential expression of genes is analyzed statistically and genes are assigned to various classes which may (or not) enhance the understanding of underlying biological processes. Alternatively, a reduced set of genes may be singled out and used as biomarkers for diagnosis and prognosis.
Microarray data is typically used both to discover new classes as well as in class prediction. Discovery of new classes [1–4] is usually achieved with the help of clustering techniques such as hierarchical clustering [5], k-means clustering [6] and self organizing maps (SOM) [7]. Class prediction, involving the assignment of labels to samples based on their expression patterns, is typically based on statistical or supervised machine learning methods. These range from the application of simple techniques such as nearest neighbor algorithms [8] to classical methods such as linear discriminant analysis [9] to more advanced techniques such as neural networks [10], support vector machines [11–13], fuzzy logic [14] and decision trees [15]. The challenge in dealing with microarray data lies in the fact that there are orders of magnitude differences between the number of samples (typically less than a hundred) and the number of genes (typically tens of thousands) that are studied. The measurements also typically contain both measurement noise as well as systemic noise. This could have a significant impact on classification accuracy. Classification must therefore be preceded by a step known as feature selection where a subset of relevant features is identified.
There are a number of advantages to feature set selection. The first lies in reducing the cost of clinical diagnosis. It is much cheaper to focus only on the expression of a few genes rather than on thousands of genes for diagnosis [16]. Feature set selection can also lead to a reduction in computational cost as a result of a reduction in problem dimensionality. Furthermore, feature set selection often gives rise to a much smaller and a more compact gene set. This could make it easier to identify genes of particular importance to the problem under study. Moreover, given the disparity in the magnitudes of the numbers of genes and samples, it is difficult to justify the development of a classifier based on a gene set where the number of genes is greater than the number of samples.
One way to categorize feature set selection approaches is to classify them as either filter (such as those based on statistical tests such as t-test, F-test etc.) or wrapper [17] methods. These methods have the advantage of having very low computational complexity as well as better generalization potential since they are uncorrelated to the learning method.
Wrapper type approaches are those in which the feature selection method is bundled together with the learning method. This implies that the usefulness of a feature is validated by the estimated accuracy of the learning method. In consequence, often, a small subset of the feature set with very high prediction accuracy can be obtained because the characteristics of the features match well with the characteristics of the learning method.
Another way of categorizing feature set selection approaches is as univariate or multivariate [18]. Univariate methods [1, 19] consider the contributions of individual genes to the classification independently. In contrast multivariate methods such as recursive feature elimination (RFE) [12], leave one out (LOO) method [13], mutual information based approaches [20] etc., measure the relative contribution of a gene to the classification by taking the effect of other genes into consideration at the same time.
A serious deficiency of currently used multivariate approaches for feature set selection is that they are based on selecting genes which are maximally relevant with respect to the classes. The problem with this approach is that there might still be genes among the selected set that are heavily correlated with each other and thus leading to a redundancy in the selected feature set. Ding et. al. [20] have used mutual information for gene selection that has maximum relevance with minimal redundancy by solving a simple two-objective optimization.
In the study presented here, a similar approach has been followed for feature set selection by trying to maximize the relevance and minimize the redundancy of the selected genes. However, normalized mutual information has been used instead of mutual information. In addition, both Battiti's greedy selection algorithm [21] as well as a simulated annealing based approach [22] have been used. In order to find a more representative subset of features, an iterative procedure was adopted that incorporates an initial clustering followed by data partitioning and the application of the algorithm to each of the partitions. A leave-one-out approach then selects the most commonly selected genes across all the different runs and the gene selection algorithm is applied again to pare down the list of selected genes until a minimal subset that gives a satisfactory accuracy of classification is obtained. The algorithm was applied to three different data sets and the results obtained were compared to work done by others using the same data sets. Additionally the algorithm was also compared to work done by Ding and Peng [20] for three different datasets.
Results
Datasets
Three public microarray data sets were used to assess the performance of the algorithm.
SRBCT data
This data set includes 88 cDNA arrays for 63 training samples and 25 test samples from [10]. All samples were combined together and the 5 non-SRBCT samples were removed. The data set consists of four types of tumors in childhood, including Ewing's sarcoma (EWS), rhabdomyosarcoma (RMS), neuroblastoma (NB), and Burkitt lymphoma (BL). After filtering by [10], 2308 genes remained in the data set. The data was transformed to natural logarithmic values. Finally, each sample was also standardized to zero mean and unit variance.
Breast cancer data
This data set contains expression levels of 7129 genes in 49 breast tumor samples from [23]. The samples were classified according to their estrogen receptor (ER) status. 25 samples were ER positive while the other 24 samples were ER negative. In the pre-processing procedure, the data was thresholded with a floor of 100 and a ceiling of 16000 Affymetrix intensity units. Then those genes with  ≤ 5 or max - min ≤ 500 were excluded. The filtered data was transformed to base 10 logarithmic values. Finally, each sample was standardized to zero mean and unit variance.
≤ 5 or max - min ≤ 500 were excluded. The filtered data was transformed to base 10 logarithmic values. Finally, each sample was standardized to zero mean and unit variance.
Colon cancer data
This data set contains expression levels of 40 tumor and 22 normal colon tissues. Only the 2000 genes with the highest minimal intensity were selected by [24]. The data waspre-processed by transforming the raw intensities to base 10 logarithmic values and standardizing each sample to zero mean and unit variance.
Results
The results of the application of the full algorithm using both the greedy selection algorithm as well as the simulated annealing algorithm for solving Problem 2 are shown in Table 1. The associated clustering dendrograms are shown in Figures 1, 3 and 5, respectively. For all the dendrograms, the samples are presented along the x-axis with the gene-set along the y-axis. Orange reflects up-expression while yellow represents no or little expression.
The results for SRBCT were the best with a 100% accuracy obtained. The number of genes selected in this case was 58 as opposed to the 96 genes selected by Khan et al. [10]. It is interesting to note that when the binary optimization algorithm was used to select genes for the SRBCT data, 50 of the genes selected were the same as those selected with the greedy algorithm. The accuracy rate for breast cancer data was similar for both cases with about 5 samples being misclassified. The final gene set for this data set contained 31 genes. For colon cancer data, there were 6 mis-classifications, with an overall accuracy rate of 90.3%. There were 29 genes in the final selected gene set.
There seems to be no quantitative or qualitative difference when using the greedy selection or the binary optimization algorithm. Moreover, since the simulated annealing procedure requires an inordinate amount of computation time (of the order of days) as compared to the greedy selection algorithm (of the order of a couple of hours), the iterative procedure was implemented with the greedy algorithm. The iterative approach shown in Figure 8 was used for all three data sets and the clustering dendrograms with the reduced feature sets are shown in Figures 2, 4 and 6 respectively. It is interesting to note that the classification accuracy is not affected by using a much reduced feature set. In fact, for colon cancer data, the accuracy improved to 91.9%.
Optimal Feature Set Selection Algorithm. The function CLUSTER uses the k-means clustering approach to partition the initial gene set into the desired number of partitions K, with G genes in each partition. K and G are user-specified. The function SELECT_GENES uses either the greedy approach (Figure 7) or the heuristic simulated annealing approach to solve Problem 2. The function CLASSIFICATION_ERROR uses kNN classification method to assess the discriminant power of the selected genes and returns the classification error.
One of the main concerns while carrying out a multi-objective optimization is the presence of the weight factor β. The selection of β is usually heuristic. Battiti suggested in [21] that the value of β between 0.5 and 1.0 is appropriate for most cases. The effect of changing β was studied by changing its value from 0 to 1 in steps of 0.2. using the colon cancer data set and the classification accuracy calculated (Table 2). A value of (0.5 – 1.0) for β seems appropriate. Also, the order of selection of the first 10 genes was examined (Table 3). It appears that varying β does affect the gene selection order to a certain extent. For example, comparing the gene selection orders for β = 0.6, 0.8 reveals that genes 267 and 513 swap places while genes 1256 (for β = 0.6) and 1727 (for β = 0.8) are not common to both cases. However, it must be kept in mind that the selection order in this case is not indicative of the relative importance of the genes since a greedy algorithm is being used.
We also compared our methodology to that of Ding and Peng [20] for three different datasets. The first dataset is the colon cancer dataset [24]. The second dataset is the leukemia dataset [1]. The third and final dataset used was the NCI dataset [25]. The results are tabulated in Table 4. As can be observed, the Uncertainity-based (UB) method (our method) seemed to do better than the DP (Ding and Peng) method for the colon dataset. On the other hand, for the leukemia dataset, DP proved superior to our method. For the NCI dataset, both methods performed poorly with the DP method having a slight edge. It must however be noted that the NCI dataset consists of 9 classes and only 60 samples. As a result, classifying the dataset with a very small sample size into 9 different classes and using only 15 genes is very difficult.
A further difficulty in comparing different methodologies lies in the fact that the initial pre-processing step could also play a role in classification accuracies. In the absence of a uniformity of preprocessing of the datasets, it is difficult to draw general conclusions regarding the relative performances of two different methodologies.
As commonly observed when analytical algorithms are compared, the performance shows mixed results. While Ding and Peng algorithm outperformed the one presented here (see table 4), it should be noted that the description of methods in their article did not allow us to compare both algorithms on equal terms as no gene ranking was provided, and thus the biological significance of their findings could not be assessed.
A comparison between the accuracies obtained by the original papers (from which the datasets were obtained) and our method is given in Table 5. The list of genes selected for each dataset and their ranks in the original papers are given in the supplementary file.
Discussion
The details of the selected genes and the comparison with the original data are listed in the supplementary material for all three data sets. This section presents a discussion of the comparison of genes selected by the algorithm presented in this work with those presented in earlier work (or as in the case of Breast cancer and SRBCT data, in the original work).
SRBCT data set
There were a total of 41 genes that overlapped between the selection methods presented in this work and those by [10]. The common genes were from all rank levels of the original method. Left out genes coded often, but not always for proteins from a functional system similar to those still selected here, as in the case of no. 233721 insulin-like growth factor binding protein (not selected here) and no. 296448 (insulin- like growth factor 2) and 207274 (insulin-like growth factor 2, exon 7 and additional ORF), which were selected by both methods. Interestingly, two viral oncogene sequences were not selected (nos. 417226 and 812965, v-myc avianmyelocytomatosis viral oncogene homologs), nor were some extra- cellular matrix associated genes (nos: 122159 and 809901, collagens type III and XV) both without replacement from similar genes. The seventeen newly selected genes that were not part of the original selection come from various functional systems. Of interest here is that while the original gene no. 245330 (Human krueppel-related zinc finger protein H-plk) was left out, gene no. 767495 (GLI-Krueppel family member GLI3) was newly selected. Such "nuclear localization signals" have been shown to be involved in processes determining proper nuclear localization [26], but may also be determinants of progression towards cancer [27].
Breast cancer data set
Out of the 31 genes selected here, 16 were not selected in the original publication [23], which selected 60 genes. The 45 genes not selected by the present method covered a large variety of physiological functions, without a specific pattern becoming obvious. Two genes linked to the ILGF were left out (no: s37730 and m62403), with no replacement. ILGF is linked to the development of a number of cancers (review in [28]). The fact that ILGF-linked genes are left out here may be discussed in two diametrically opposite ways. For once, leaving these genes out of the classification set may cause an oversight of the tissue's potential to induce further cancerous growth. More likely, though, it seems like whatever physiological role these genes play in the tissue, they do not contribute to distinguishing between various types of cancer.
Colon cancer data set
Contrary to the other two test sets, in the case of colon cancer, the original publication did not rank the gene set retrieved, so that a direct comparison of results was not possible. The same dataset, however, has been re- analyzed previously by Silvio Bicciato [29], using an auto associative neural network model, which yielded a ranked gene list. With the exception of Tetraspan-1, which heads the rank list with a weight of 0.9391, the top genes found by Bicciato for the reconstruction of the normal class concur with the rank list presented here, while only one gene (Heat shock 60 kD protein 1) is selected by both methods when compared to the gene list in [29] for the reconstruction of the tumor class. This tetraspan family of proteins is involved in cell adhesion processes at the gap junctions and one related protein was enhanced in highly metastatic gastric cancer [30].
Conclusion
Compared to the classification methods described in the original articles or previous third party analysis, the algorithm described here compares favorably in its capacity to select small sets of genes that distinguish between various cancer types. The observation that it leaves out several genes known to be involved in cancer development may indicate that this method's advantage lies more in good classification, but not in the detection of new dysfunctional regulatory mechanisms.
Although preliminary results using a greedy selection algorithm are encouraging, additional work needs to be done in order to develop alternative methodologies for multi-objective optimization that can select a more optimal and representative set of genes for discriminating between various cancer sub-types.
Methods
Algorithms for microarray data analysis typically focus on obtaining a set of genes that can distinguish between the different classes in a given sample set. Thus, the primary concern is to ensure the relevance of the genes to the classes under consideration.
Given a microarray data set with m samples belonging to k known classes and n genes, we want to select out those genes which are able to predict the differences in the gene expression patterns in different sample classes. Define  ; |c| = k, as the vector labeling the classes of samples and
; |c| = k, as the vector labeling the classes of samples and  ; i ∈ n as the gene expression profile of gene i. Let
; i ∈ n as the gene expression profile of gene i. Let  be the feature set of all genes and let S be the set of selected genes. Then, the feature set selection problem can be defined as follows:
be the feature set of all genes and let S be the set of selected genes. Then, the feature set selection problem can be defined as follows:
Problem 1
Select a set S of genes, S ⊂  such that ∀ gene s ∈ S the relevance of s with
such that ∀ gene s ∈ S the relevance of s with  is maximized.
is maximized.
However, the feature set of genes selected will contain a number of redundant genes with sometimes little relevance to the classes. This is due to the fact that the presence of genes that are closely related to each other imply that there is a possibility of genes orthoganal to those in the selected set being left out of the final feature set. Moreover, the presence of genes with little relevance to the classes leads to a reduction in the "useful information".
Ideally, selected genes should have high relevance with the classes while the redundancy among the selected genes is low. Most previous studies emphasized the selection of highly relevant genes. Ding et. al. [20] addressed the issue of the redundancies among the selected genes. The genes with high relevance are expected to be able to predict the classes of the samples. However, the prediction power is reduced if many redundant genes are selected. In contrast, a feature set that contains genes not only with high relevance with respect to the classes but with low mutual redundancy is more effective in its prediction capability.
Problem formulation
To assess the effectiveness of the genes, both the relevance and the redundancy need to be measured quantitatively. An entropy based correlation measure is chosen here. According to Shannon's information theory [31], the entropy of a random variable X can be defined as:

Entropy measures the uncertainty of a random variable. For the measurement of the interdependency of two random variables X and Y, some researchers [20, 21] used mutual information, which is defined as:
I(X, Y) = H(X) + H(Y) - H(X, Y) (2)
In order to ensure that different values are comparable and have similar effects, normalized mutual information is used as a measure and is defined as:

U(X, Y) is symmetrical and ranges from 0 to 1, with the value 1 indicating that the knowledge of one variable completely predicts the other (high mutual relevance) while the value 0 indicates that X and Y are independent (low mutual relevance).
The mutual relevance between

and  can then be modeled by U (
can then be modeled by U (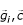 ) while the dependency between two genes is U (
) while the dependency between two genes is U ( ).
).
The total relevance of all selected genes is given by

The total redundancy among the selected genes is given by

Therefore, the problem of selecting genes can be reformulated as follows:
Problem 2
Select a set S of genes, S ⊂  such that ∀ g
i
∈ S, the total relevance of all the selected genes with
such that ∀ g
i
∈ S, the total relevance of all the selected genes with  , J1, is maximized while the total relevance among all the selected genes g
i
∈ S, J2, is minimized.
, J1, is maximized while the total relevance among all the selected genes g
i
∈ S, J2, is minimized.
This is a two-objective optimization problem. To solve it, a simple way is to combine these two objectives into one:

where β is a weight parameter.
subsection* Algorithm
To solve the above problem, Battiti [21] proposed a greedy algorithm. The procedure can be described as follows (see Figure 7):
-
1.
Initialization: F ← allgenes, S ← ∅.
-
2.
First gene: select gene i that has highest relevance U (
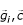 ). g
i
∈ S, F \ i.
). g
i
∈ S, F \ i. -
3.
Remaining genes: From F, select gene j that maximizes
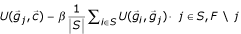 .
. -
4.
Repeat the above step until the desired number of genes are obtained.
The maximization problem (6) can also be re-formulated into a binary optimization problem. Let x i be a binary variable with value 1 for selecting gene i while value 0 for not. Thus, Equation (6) can be rewritten into:

It can be further rewritten into matrix form:
max U c Tx - β xTU p x (8)
where U c is the relevance vector, U p is matrix of pairwise redundancy.
Beasley et al. [32] discussed several heuristic algorithms to solve such binary quadratic programming problems. A heuristic simulated annealing method was employed to solve the problem. The pseudo codes of simulated annealing can be obtained from [32].
There are however limitations to both approaches. There is a possibility that the solution obtained for Problem 2 can lead to a local optimum. This could result in a sub-optimal feature set thereby affecting the prediction accuracy. In order to expand the search space, an iterative procedure was adopted. The data was initially clustered and partitioned into K groups, C1, C2,..., C K by using k-means clustering. The idea was to group genes with similar expression patterns together. The greedy or heuristic simulated annealing procedure was then applied to select a subset of genes, S k , from each partition, k, such that the selected genes had low mutual relevance with respect to each other while at the same having maximal relevance with the different classes. The genes selected from each subset are then combined to obtain a single gene set, that is, S = S1 ⋃ S2 ⋃ S3,..., ⋃S K .
The final set of genes is selected by carrying out a leave-one-out cross validation (LOOCV). For each run, one sample is held out for testing whilei the remaining N - 1 samples are used to train the classifier. The genes are selected by the algorithm using the training samples and then are used to classify the testing sample. The overall accuracy rate is calculated based on the correctness of the classifications of each testing sample. In order to get a deeper understanding of the selected genes, those genes found in common for all the N different runs of the LOOCV experiment are finally listed out for further investigation. The process of gene selection is repeated by selecting a subset of genes from this feature set, that gives a classification error that is below a user defined threshold ε. Nearest neighborhood (k-NN) classification method is used to assess the discriminant power of the selected genes by the method. The process is stopped when the error becomes greater than ε. The full algorithm is presented in Figure 8.
References
Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA, et al.: Molecular classification of Cancer:class discovery and class prediction by gene expression monitoring. Nature 1999, 286: 531–537. 10.1126/science.286.5439.531
Alizadeh AA, Eisen MB, Davis RE, Ma C, Lossos IS, Rosenwald A, Boldrick JC, Sabet H, Tran T, Yu X, et al.: Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature 2000, 403: 503–511. 10.1038/35000501
Bittner M, Meltzer P, Chen Y, Jiang Y, Seftor E, Hendrix M, Radmacher M, Simon R, Yakhini Z, Ben-Dor A, et al.: Molecular classification of cutaneous malignant melanoma by gene expression profiling. Nature 2000, 406: 536–540. 10.1038/35020115
Perou CM, Sorlie T, Eisen MB, van de Rijn M, Jeffrey SS, Rees CA, Pollack JR, Ross DT, Johnsen H, Akslen LA, et al.: Molecular portraits of human breast tumours. Nature 2000, 406: 747–752. 10.1038/35021093
Weinstein JN, Myers TG, O'Connor PM, Friend SH, Fornace AJ, Kohn KW, Fojo T, Bates SE, Rubinstein LV, Anderson NLea: An informatio-intensive approach to the molecular pharmacology of cancer. Science 1997, 275: 343–349. 10.1126/science.275.5298.343
Tavazoi S, Hughes JD, Campbell MJ, Cho RJ, Church GM: Systematic determination of genetic network architecture. Nature Genetics 1999, 22: 281–285. 10.1038/10343
Tamayo P, Slonim D, Mesirov J, Zhu Q, Kitareewan S, Dmitrovsky S, Lander ES, Golub TR: Interpreting patterns of gene expression with self-organizing maps: methods and application to hematopoietic differentiation. National Academy of Sciences 1999, 96: 2907–2912. 10.1073/pnas.96.6.2907
Dudoit S, Fridlyand J, Speed T: Comparison of discriminantion methods for the classification of tumors using gene expression data. In Tech rep. University of Carlifornia, Berkeley; 2000.
Xiong M, Li W, Zhao J, Jin L, Boerwinkle E: Feature (Gene) Selection in Gene Expression-Based Tumor Classification. Molecular Genetics and Metabolism 2001, 73: 239–247. 10.1006/mgme.2001.3193
Khan J, et al.: Classification and diagnostic prediction of cancers using gene expression profiling andartificial neural networks. Nature Medicine 2001, 7(6):673–679. 10.1038/89044
Furey TS, Cristiani N, Duffy N, Bednarski DW, Schummer M, Haussler D: Support vector machine classification of cancer tissue samples using microarray expression data. Bioinformatics 2000, 16: 906–914. 10.1093/bioinformatics/16.10.906
Guyon I, Weston J, Barnhill S, Vapnik V: Gene selection for cancer classification using support vector machines. Machine Learn 2002, 46: 389–422. 10.1023/A:1012487302797
Mukherjee S, Tamayo P, Slonim D, Verri A, Golub T, Messirov JP: Support vector machine classification of microarray data. AI memo. CBCL paper 182. MIT Press, Cambridge, MA; 2000.
Ohno-Machado L, Vinterbo S, Weber G: Classification of gene expression data using fuzzy logic. Journal of Intelligent and Fuzzy Systems 2002, 12(1):19–24.
Cai J, Dayanik A, Yu H, Hasan N, Terauchi T, Grundy W: Classification of gene cancer types by support vector machines using microarray gene expression data. International Conference on Intelligent Systems for Molecular Biology 2000.
Xu M, Setiono R: Gene selection for cancer classification using a hybrid of univariate and multivariate feature selection methods. Applied Genomics and Proteomics 2003, 2(2):79–91.
Kohavi R, John G: Wrapper for feature subset selection. Artificial Intelligence 1997, 97(1–2):273–324. 10.1016/S0004-3702(97)00043-X
Liu H, Motoda H: Feature selection for knowledge discovery and data mining. Boston, Kluwer Acad. Publishers; 1998.
Slonim D, Tamayo P, Mesirov J, Golub T, Lander E: Class prediction and discovery using gene expression data. In 4th Annual International Conference on Computational Molecular Biology (RECOMB), 2000 Apr 8–11; Tokyo, Japan. Tokyo: Universal Academy Press; 2000:263–272.
Ding C, Peng H: Minimum Redundancy feature selection from microarray gene expression data. Computational Systems Bioinformatics 2003.
Battiti R: Using Mutual Information for Selecting Features in Supervised Neural Networks. IEEE transactions on neural networks 1994., 5(4):
Kirkpatrick S, Gelatt C, Vecchi M: Optimization by simulated annealing. Science 1983, 220: 671–680.
West M, et al.: Predicting the clinical status of human breast cancer by using gene expression profiles. Proc Natl Acad Sci USA 2001, 98(20):11462–11467. 10.1073/pnas.201162998
Alon U, et al.: Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissuesprobed by oligonucleotide arrays. Proc Natl Acad Sci USA 1999, 96(12):6745–6750. 10.1073/pnas.96.12.6745
Ross DT, Scherf Ut: Systematic variation in gene expression patterns in human cancer cell lines. Nature Genetics 2000, 24(3):227–234. 10.1038/73432
Quadrini K, Bieker J: Kruppel-like zinc fingers bind to nuclear import proteins and are required for efficient nuclear localization of erythroid Kruppel-like factor. J Biol Chem 2002, 277(35):32243–32252. 10.1074/jbc.M205677200
Zhang F, White R, Neufeld K: Phosphorylation near nuclear localization signal regulates nuclear import of adenomatous polyposis coli protei. Proc Natl Acad Sci 2000, 97(23):12577–12582. 10.1073/pnas.230435597
Renehan A, Zwahlen M, Minder C, O'Dwyer S, Shalet S, Egger M: Insulin-like growth factor(IGF)-I, IGF binding protein-3, and cancer risk. Systematic Review and Meta-Regression Analysis, Lancet 2004, 363(9418):1346–1353.
Bicciato S, Pandin M, Didone G, Bello CD: Pattern Identification and Classification in Gene Expression Data Using an Autoassociative Neural Network Model. Biotechnology and bioengineering 2003, 81(5):594–606. 10.1002/bit.10505
Lee S, Baek M, Yang H, Bang Y, Kim W, Ha J, DK K, DI J: Identification of genes differentially expressed between gastric cancers and normal gastric mucosa with cDNA microarrays. Cancer Letters 2002, 184(2):197–206. 10.1016/S0304-3835(02)00197-0
Shannon CE, Weaver W: The Mathematical Theory of Communication. University of Illinois Press; 1949.
Beasley JE: Heuristic algorithms for the unconstrained binary quadratic programming problem. London, England 1998.
Acknowledgements
The authors would like to thank the anonymous reviewers for their suggestions and critical reviews of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
LXX was responsible for the development and implementation of the algorithm as well as for writing parts of the paper. AK was involved in algorithm development as well as in writing the manuscript. AM was responsible for the analysis of the results as well as manuscript preparation. All authors read and approved the manuscript.
Electronic supplementary material
12859_2004_401_MOESM1_ESM.pdf
Additional File 1: Selected Genes for All Datasets. The file contains the list of selected genes for each of the three datasets used in this study as well as the corresponding ranks of those selected genes in the original papers. (PDF 45 KB)
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
About this article
Cite this article
Liu, X., Krishnan, A. & Mondry, A. An Entropy-based gene selection method for cancer classification using microarray data. BMC Bioinformatics 6, 76 (2005). https://doi.org/10.1186/1471-2105-6-76
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2105-6-76








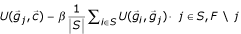 .
.