- Methodology article
- Open access
- Published:
The impact of measurement errors in the identification of regulatory networks
BMC Bioinformatics volume 10, Article number: 412 (2009)
Abstract
Background
There are several studies in the literature depicting measurement error in gene expression data and also, several others about regulatory network models. However, only a little fraction describes a combination of measurement error in mathematical regulatory networks and shows how to identify these networks under different rates of noise.
Results
This article investigates the effects of measurement error on the estimation of the parameters in regulatory networks. Simulation studies indicate that, in both time series (dependent) and non-time series (independent) data, the measurement error strongly affects the estimated parameters of the regulatory network models, biasing them as predicted by the theory. Moreover, when testing the parameters of the regulatory network models, p-values computed by ignoring the measurement error are not reliable, since the rate of false positives are not controlled under the null hypothesis. In order to overcome these problems, we present an improved version of the Ordinary Least Square estimator in independent (regression models) and dependent (autoregressive models) data when the variables are subject to noises. Moreover, measurement error estimation procedures for microarrays are also described. Simulation results also show that both corrected methods perform better than the standard ones (i.e., ignoring measurement error). The proposed methodologies are illustrated using microarray data from lung cancer patients and mouse liver time series data.
Conclusions
Measurement error dangerously affects the identification of regulatory network models, thus, they must be reduced or taken into account in order to avoid erroneous conclusions. This could be one of the reasons for high biological false positive rates identified in actual regulatory network models.
Background
There has been an increasing interest among bioinformaticians in the problem of quantifying correctly gene expression in a given sample. It is well accepted that the observed gene expression value is a combination of the "true" gene expression signal with intrinsic biological variation (natural fluctuation) and a variation caused by the measuring process, also known as measurement error. Studies have documented the presence of sizable measurement error in data collected mainly from microarrays and also by other approaches such as Real Time RT-PCR, Northern blot, CAGE, SAGE, etc [1, 2]. This measurement error can be easily observed when two technical replicates are plotted in a MA (M is the logarithm of the intensity ratio and A is the mean of the logged intensities for a dot in the plot) or scatter plots. Frequently, a considerable dispersion can be observed. This dispersion is due to the measurement error, since, in theory, technical replicates (same samples) must present the same quantifications. In general, these fluctuations are derived from probe sequence, hybridization problems, high background fluorescence, signal quantification procedures (image analysis), etc [3, 4]. In the last few years, a considerable number of reports on the problem of quantifying and separating "true" gene expression signal from noise [5–7] has been published with the main aim to find differentially expressed genes [8, 9]. Despite these results in gene expression analysis and a large amount of research performed in modeling regulatory networks (Bayesian networks [10, 11], Boolean networks [12, 13], Relevance networks [14], Graphical Gaussian models [15], Differential equations [16], etc), only a fraction of the statistical studies use procedures designed for modeling networks taking into account measurement error.
Frequently, Ordinary Least Squares (OLS) and methods related to it, such as Pearson and Spearman correlations [17], ridge, lasso and elastic net regressions [18] are widely used as estimators to quantify the strength of association between gene expression signals and model regulatory network structures. In the time series context, estimation process of Autoregressive (AR) [19–22] models also use OLS to identify which gene is or is not Granger causing another gene. Generally, a regression is carried out between the target gene and its potential predictors in order to test which predictor gene has, at a gene expression level, association with the target gene.
It is well known in the statistical literature that, when the measurement errors are ignored in the estimation process, OLS and its variants become inconsistent (i.e., even increasing the sample size the estimates do not converge to the true values). More precisely, the estimation of the slope parameters is attenuated [23] and consequently, regulatory network models become biased. Moreover, there is no control of type I error since standard OLS was not designed to treat measurement error. In this context, an adequate inference treatment must be considered for the model parameters in order to avoid inconsistent estimators. Usually, measurement equations are added to the model to capture the measurement errors effect, therefore, producing consistent estimators, efficient and asymptotically normally distributed. A careful and deep exposition on the inferential process is presented in [23] and the references therein. Although there are studies referring to problems caused by measurement errors in the statistical literature, there is a gap in the network modeling theory which must be filled in to avoid misinterpretation and distort conclusions from the inferential process. Here, we focus on the development and present some important statistical tools to be applied in OLS-based and VAR network models taking into account the measurement errors effect. We also conduct simulation studies in order to evaluate the impact of the measurement error in the identification of gene regulatory networks using the standard OLS in both conditions, time series and non time series data. Surprisingly, both the simulations and theory described that, in the presence of measurement error, the estimated coefficients are biased even increasing the amount of observations, and the statistical tests are not controlling the rate of false positives properly. These results were also observed in time series context, where the autoregressive coefficients were strongly affected. Thus, a corrected version of the OLS estimator for independent (in the regression context) and dependent (in the autoregressive context) data containing measurement error were developed. Results in both, simulated and actual biological data are illustrated. Moreover, two procedures to estimate measurement error in microarrays are presented.
Results and discussions
In order to evaluate the performance of conventional OLS and VAR methods in practice, simulations were carried out in artificial data with absence and presence of measurement error. Noise was added at different rates, and sample size was increased in order to evaluate the consistence of conventional and proposed approaches.
In the following we give a brief explanation about the usual and proposed methods. Let x and y be variables (gene expression values) with the following relationship y = α + βx + ε, where ε is the random error (intrinsic biological variation) of the model with zero mean and finite variance. In general, we are interested in estimating the parameters α and β to make inferences about them. In practice, we take a sample x i , y i for i = 1,..., n and use these quantities to obtain estimates for the parameters of interest. However, it is not always possible to observe directly the values of x and y because sometimes they are latent values, i.e., they are masked by measurement errors derived by the measurement process in microarrays, for example. Then, instead of observing the true variables, we observe surrogate variables X and Y which carry an error, that is X = x + ϵ1 and Y = y + ϵ2, where ϵ1 and ϵ2 are measurement errors. Generally, what is done in practice is a naive solution, since it simply replaces x with X and y with Y in the regression equation and uses the OLS approach to estimate the parameters. That is, based on the equation Y = α + βX + ε, estimators are built. On the other hand, the proposed approach is slightly different. The latter considers three equations, namely: y = α + βx + ε, X = x + ϵ1 and Y = y + ϵ2 and uses them to estimate the model parameters. This little difference can result great impact in the estimators properties of each approach. Notice that the former produces inconsistent estimators and the latter produces consistent estimators when the data contains measurement error. The same idea can be applied in the time series context.
The corrected versions of the OLS estimators in both independent and dependent data were compared to their conventional forms in order to evaluate the performance under gene expression data containing measurement error. The standard OLS and VAR models are particular cases of the proposed models in the case when the measurement error is absent. Firstly, simulations were performed in regression models. Table 1 illustrates average coefficients estimated by standard OLS in 10,000 Monte Carlo simulations. Notice that increasing the rate of measurement error, more attenuated become the estimated coefficients, i.e., the estimates are shifted towards zero. Table 2 illustrates the percentage of rejected hypotheses in 10,000 Monte Carlo simulations. Analyzing when β1 = 0, i.e., when there is no association between the corresponding covariate and the response variable, Table 2 shows that the OLS approach does not control, at a 5% nominal level, the rate of false positives. The larger the sample size, the worst the OLS performance, as it was expected to be. On the other hand, the coefficients of the corrected OLS are unbiased (Table 1 - values between brackets) and converge to "true" value when sample's size becomes larger. Moreover, the rate of false positives are actually controlled under the null hypothesis (Table 2 - values between brackets).
Analyzing Figure 1A, we conclude that, the standard OLS is not controlling the rate of false positives in the presence of measurement error for any significance level (p-value threshold). On the other hand, Figure 1B describes the consistency of the test performed by the corrected OLS, i.e., the uniform distribution of p-values illustrates that the rate of false positives is actually controlled under any considered threshold, since the uniform distribution emerges for p-values when the distribution of the statistic is correctly specified (otherwise, the p-value distribution may not be uniform).
P-value distribution under the null hypothesis ( β 1 = 0) in independent data with standard deviation of the measurement error equal to 0.6 and sample size equal to 400 (model described in Simulations section, simulation I). This simulation was performed 10,000 times. (A) Standard Ordinary Least Squares (non uniform distribution); (B) Corrected Ordinary Least Squares (uniform distribution).
In the time series case, similar results were observed. The standard VAR estimates produce biased coefficients in the presence of measurement error (Table 3). Moreover, there is no control of the type I error in both, autoregressive and cross-autoregressive coefficients (in all the text, in order to simplify the notation, autoregressive coefficient will denote the auto-loop, i.e., the coefficient related to zi, t-r→ zi, tand cross-autoregressive coefficient will represent the coefficient for zj, t-r→ zi, t, where i ≠ j and r <t) (Table 4). Analyzing the results produced by the proposed VAR model (Table 3 - values between brackets), it is possible to observe that the estimated coefficients converge to the true value as time series length increases. Notice that, the results produced by the standard VAR model indicate that, increasing the sample size does not imply in convergence of the estimates to the true values (Table 3). By observing Table 4, we see that the corrected VAR approach is actually controlling the rate of false positives in the set significance level (p < 0.05). Figure 2 emphasizes this result. Figure 2A and 2B describe the p-value distributions of autoregressive and cross-autoregressive coefficients of standard VAR under the null hypothesis (β0 = 0 (autoregressive) and β1 = 0 (cross-autoregressive)). Notice that when β0 = β1 = 0, the p-value distributions should be uniform in the interval [0,1]. However, there is a high concentration around zero, demonstrating that the rates of false positives are inflated (and consequently not controlled) in both autoregressive or cross-autoregressive cases. In Figures 2C and 2D, the p-value distributions are uniform, i.e., the test under the null hypothesis (β0 = 0 and β1 = 0) using the corrected VAR model is actually controlling the type I error in autoregressive and cross-autoregressive coefficients (uniform distribution). Figures 3 and 4 illustrates the corrected power curves for both, OLS and VAR. The corrected power curve Pc(α) can be defined as
P-value distribution under the null hypothesis in time series data with standard deviation of the measurement error equal to 0.6 and time series length equal to 400 (model described in Simulations section, simulation II). This simulation was performed 10,000 times. (A) Standard VAR p-value distribution of autoregressive coefficient β0 = 0 (non uniform distribution); (B) Standard VAR p-value distribution of cross-autoregressive coefficient β1 = 0 (non uniform distribution); (C) Corrected VAR p-value distribution of autoregressive coefficient β0 = 0 (uniform distribution); (D) Corrected VAR p-value distribution of cross-autoregressive coefficient β1 = 0 (uniform distribution).
Corrected power curve. The full line represents the proposed OLS and the dashed line represents the standard OLS. It was performed 15,000 Monte Carlo simulations (model described in simulation I) for each n where n varied from 300 to 1,000 in steps of 100. n: sample size. P-value and standard deviation of measurement error were set to 0.05 and 0.5, respectively.
Corrected power curve. The full line represents the proposed VAR and the dashed line represents the standard VAR. It was performed 15,000 Monte Carlo simulations (model described in simulation II) for each n where n varied from 300 to 1,000 in steps of 100. n: sample size. P-value and standard deviation of measurement error were set to 0.05 and 0.5, respectively.

where α is the adopted type I error nominal level, P(a(α)) is the power using the true probability of the type I error, namely a(α). Notice that the corrected power is just the power penalized by the distance between a(α) and α. This correction in the power is necessary because under the null hypothesis, the power has to be the nominal level, and for comparing powers from different statistics it must be done using the same nominal level.
For a good statistic, notice that under an alternative hypothesis and when n → ∞, the corrected power Pc(α) converges to one because  and
and  . On the one hand, for a statistic that does not control the rate of false positives, for example, when α is set to 5% and the true probability of the type I error is a(α) = 0.08, since a(α)/α is greater than one, Pc(α) will not converge to one. On the other hand, for a good statistic, the rate a(α)/α converges to one when n → ∞, then Pc(α) will converge to one. Analyzing Figures 3 and 4, it is possible to verify that, for standard OLS and VAR approaches (dashed lines), the ratio a(α)/α increases faster than the corresponding powers P(a(α)), i.e., the dashed lines is decreasing as n increases. Notice on Tables 2 and 4 that the rates of false positives (a(α)) increase as n increases, and consequently, in our specific case, the ratio a(α)/α increases and the corrected power Pc(a(α)) converges to zero. On the other hand, the proposed methods (full lines) keep the false positive rates controlled while the corrected power increases as n increases. It can be observed by the full lines converging to one (Figures 2 and 4) and also on Tables 2 and 4. The variations present in the curves are probably due to variations in Monte Carlo simulations, since these variations decreased (become smoother) when the number of simulations was increased from 5,000 to 10,000 and from 10,000 to 15,000. In order to illustrate the performance of standard and corrected OLS and VAR approaches in actual biological data, firstly, the measurement error was estimated using the method described in the Measurement error estimation section (No technical replicates subsection). Then, the TP53 network was constructed using a dataset composed of 400 microarrays.
. On the one hand, for a statistic that does not control the rate of false positives, for example, when α is set to 5% and the true probability of the type I error is a(α) = 0.08, since a(α)/α is greater than one, Pc(α) will not converge to one. On the other hand, for a good statistic, the rate a(α)/α converges to one when n → ∞, then Pc(α) will converge to one. Analyzing Figures 3 and 4, it is possible to verify that, for standard OLS and VAR approaches (dashed lines), the ratio a(α)/α increases faster than the corresponding powers P(a(α)), i.e., the dashed lines is decreasing as n increases. Notice on Tables 2 and 4 that the rates of false positives (a(α)) increase as n increases, and consequently, in our specific case, the ratio a(α)/α increases and the corrected power Pc(a(α)) converges to zero. On the other hand, the proposed methods (full lines) keep the false positive rates controlled while the corrected power increases as n increases. It can be observed by the full lines converging to one (Figures 2 and 4) and also on Tables 2 and 4. The variations present in the curves are probably due to variations in Monte Carlo simulations, since these variations decreased (become smoother) when the number of simulations was increased from 5,000 to 10,000 and from 10,000 to 15,000. In order to illustrate the performance of standard and corrected OLS and VAR approaches in actual biological data, firstly, the measurement error was estimated using the method described in the Measurement error estimation section (No technical replicates subsection). Then, the TP53 network was constructed using a dataset composed of 400 microarrays.
Table 5 illustrates the results of a multivariate regression using OLS. Four genes known to be direct targets of TP53 were selected, namely, MDM2, FAS, BAX and MAP4, and a multivariate network was constructed using OLS. In fact, these four genes were actually identified as targets of TP53 (high t-statistics). Notice that comparing the standard and corrected OLS estimators, it is possible to conclude that the t-statistics are different probably due to the biased standard OLS estimator in the presence of measurement error.

Table 6 shows the application of both, standard and proposed VAR models in a set of well known five genes related to circadian rhythm, namely, CLOCK, CRY2, PER2, PER3 and DBP. The genes CRY2, PER2, PER3 and DBP are known to be regulated by the complex BMAL1-CLOCK in mammals [24]. A VAR process of order one was adjusted and applied in a multivariate manner. Notice that also in the time series data, the estimators presented different results due to measurement error.

Comparison of the usual and proposed methods in actual biological data is a difficult task since no one knows the "true" values. However, as observed in the simulation results, it is possible to conclude that the corrected approaches provide more reasonable results than biased standard methods.
In order to uncover more details about the performance of both, OLS and VAR, other experiments were conducted. These experiments consist in adding correlation in the residues and testing other null hypothesis (data not shown). The results obtained ignoring the errors by these methods can be compiled as:
-
1.
in both, independent and time series data, standard OLS does not work correctly in the presence of measurement error and correlated residues;
-
2.
in the presence of measurement error and no correlation among all predictors of independent data, the t-test built, under the standard OLS approach, to test H0 : β j = m for j = 1,..., p works perfectly only if m = 0 (for other null hypothesis this t-test does not work correctly). This happens because, under this hypothesis, there is no covariate effect and, consequently, there is no measurement error effect associated with the covariate. The same behavior can be seen in Patriota et al. (2009) [25];
-
3.
in the time series case, the t-test (or Wald's test) does not control the type I error rate in the presence of measurement error, independent whether there is or not correlation between time series;
-
4.
in the presence of measurement error, the estimates obtained by standard OLS are always attenuated.
Therefore, these results demonstrate that improved methods to construct regulatory networks become necessary, since it is known that genes belong to an intrincate network, i.e., the covariates may be correlated and, moreover, gene expression quantification processes such as microarray technology measure with considerable error. If these conditions are ignored, one may obtain distort results and, consequently, conclude that there is a relationship between gene expressions where there is no association.
Construction of large networks is a challenge in bioinformatics. The methods proposed here do not allow the identification of networks when the number of variables is larger than the number of observations. Increasing the number of variables, the estimates become imprecise and the chances of obtaining multicollinearity problems also increases. In the presence of multicollinearity, one may use a feature selection procedure such as a stepwise (forward or backward, for example) in order to choose the optimum set of predictors.
Analyzing Pearson correlation coefficient, one can observe that it is simply a normalized linear regression coefficient (OLS) between -1 and 1. Therefore, Pearson correlation-based methods such as Relevance networks [14] or Graphical Gaussian models [26] need further studies in order to evaluate if they are also super-estimating the rate of false positives and attenuating the coefficients like OLS. Moreover, Pearson correlation is widely used in order to test linear correlation between a certain gene expression signal and another characteristic such as prognostic, phenotype, tumor grade etc. Since these covariates may be measured with error, it is also crucial to develop a corrected Pearson correlation.
In order to develop a corrected Pearson correlation for measurement error, verify that it is possible to use the improved OLS presented in this report. The corrected Pearson correlation (ρ) between two random variables X and Y, both measured with error is given by

where β should be estimated by using the corrected OLS (i.e., by simultaneously considering the three equations: y = α + βx + ε, X = x + ϵ1 and Y = y + ϵ2), σ
X
and σ
Y
are the standard deviations of the observed variables X and Y, respectively, and  and
and  are the standard deviations of the error of measure ϵ1 and ϵ2, respectively. In this way, the estimate of the corrected version of the Pearson correlation is consistent (the larger the sample size, the smaller estimation error tends to be). Notice that, the difference between the corrected and uncorrected version of the Pearson correlation is that we are removing the excess of variability from the estimated variances of the latent x and y, since the sample variances of X and Y always over-estimate them due to the measurement errors ϵ1 and ϵ2 (note that,
are the standard deviations of the error of measure ϵ1 and ϵ2, respectively. In this way, the estimate of the corrected version of the Pearson correlation is consistent (the larger the sample size, the smaller estimation error tends to be). Notice that, the difference between the corrected and uncorrected version of the Pearson correlation is that we are removing the excess of variability from the estimated variances of the latent x and y, since the sample variances of X and Y always over-estimate them due to the measurement errors ϵ1 and ϵ2 (note that,  and
and  ), where
), where  and
and  are the variances of x and y, respectively.
are the variances of x and y, respectively.
Although the examples provided here only treat regulatory network models, the proposed approaches can be applied in a straightforward manner also to estimate linear relationships between random variables measured with error.
Conclusions
Unfortunately, avoiding measurement error in a complete manner is a very difficult task, however, it can be minimized in the measuring (experimental) process and treated during the data analysis step. Here, we have shown evidence that presence of the measurement errors has a high impact in regulatory network models. In order to overcome this problem, approaches in both major data conditions, independent and time series data were proposed in addition to measurement error estimation procedures. Further studies are necessary in order to verify how is the performance of other regulatory networks (Bayesian networks, Structural Equation models, Graphical Gaussian models, Relevance networks, etc) in the presence of measurement error.
Methods
In this section, standard Ordinary Least Squares and Vector Autoregressive models will be described. Furthermore, corrected methods for measurement error will also be presented. Finally, the model used in the simulations will be detailed.
Ordinary least squares
In a multivariate regression model, let x1, x2,..., x p be p predictor variables (genes) possibly being related to a response variable y (gene). The conventional linear regression model states that gene y is composed of an intercept or constant a which is the basal expression level of y, the predictors or gene expressions x j 's (j = 1,..., p) which relationship with y is represented by β = (β1,..., β p )⊤ (the sign of β j represents the relationship between y and x j , i.e., positive or negative association), and a random error ε, which accounts for an intrinsic biological variation (this is not the measurement error).
With n independent observations (microarrays) y and the associated gene expression values of x j , the complete model becomes

for i = 1,..., n. In matrix notation, it is described as

where





The entire vector of error terms, ε i = (εi 1,..., ε iq )⊤, are assumed to be independent and identically distributed as a q-variate normal distribution with zero vector mean and positive definite covariance matrix Σ ε for all i = 1,..., n, where q is the number of response variables. Notice that the proposed method is considering the homoscedastic case, i.e., the covariance matrix Σ ε does not change with i. Let Σ yx , Σ xx and Σ yy be the covariances of (y, x), (x, x) and (y, y), respectively. These covariance matrices could be estimated by:


and

where

and

Then, the intercept α is estimated as

and the estimator for the model's coefficient is given by

The asymptotic variance-covariance matrix of vec( ) and its estimate are given, respectively, by
) and its estimate are given, respectively, by

and

where ⊗ is the Kronecker product and  (non biased estimator). Notice that, the diagonal elements of
(non biased estimator). Notice that, the diagonal elements of  are the variances of the elements of
are the variances of the elements of  , say
, say  for j = 1,..., p.
for j = 1,..., p.
Let  denote the fitted values of y, then, the residuals are
denote the fitted values of y, then, the residuals are

Hypothesis testing
The main interest in a simple regression model (y i = α + β x i + ε i ) lies in testing the strength of the relationship between the predictor variable (gene) x and the response variable (gene) y, in other words, if β is equal to a certain value m (in general, m = 0, i.e., there is or not linear relationship between genes x and y).
The asymptotic distribution of vec( ) is given by
) is given by

and the test is described by:

This test may be performed using the Wald-type statistic expressed as

where C is a matrix of contrasts (usually, C = I). For more details about the matrix of contrasts, see [27]. Under the null hypothesis, (20) has a limit χ2(d) distribution, where d = rank(C) gives the number of linear restrictions.
Ordinary least squares with measurement error
Now, we shall study models of the regression type where one is unable to observe expression values of genes x and y (as described before) directly. Instead of observing x and y, one observes the sum

and

with

where ϵ1 ~ N(0,  ) independent of ϵ2 ~ N(0,
) independent of ϵ2 ~ N(0,  ) with
) with  and
and  known are called as measurement errors, i.e., the variation derived by the measurement process (for example, the measurement error introduced when analyzing microarrays), ε ~ N(0, Σ
ε
) is the random error (intrinsic biological variation) and x ~ N (μ
x
, Σ
xx
), y ~ N(μ
y
, Σ
yy
) with μ
y
= α + βμ
x
and Σ
yy
= β Σ
xx
β⊤ + Σε.
known are called as measurement errors, i.e., the variation derived by the measurement process (for example, the measurement error introduced when analyzing microarrays), ε ~ N(0, Σ
ε
) is the random error (intrinsic biological variation) and x ~ N (μ
x
, Σ
xx
), y ~ N(μ
y
, Σ
yy
) with μ
y
= α + βμ
x
and Σ
yy
= β Σ
xx
β⊤ + Σε.
The matrices  and
and  are given by
are given by

and

i.e., the measurement errors may be different for each variable. Notice that the components of the measurement error's vector may be correlated but the entire vectors are independent.
Let Σ YX , Σ XX and Σ YY be the sample covariances of (Y, X), (X, X) and (Y, Y), respectively. These covariance matrices could be estimated by substituting x and y by X and Y in equations (8-12). Then, the intercept a is estimated as

and the estimator for the model's coefficient is given by

where

Notice that  is estimated using equation (10) and
is estimated using equation (10) and  must be known a priori (it can be estimated using the procedures described in the section "Measurement errors estimation").
must be known a priori (it can be estimated using the procedures described in the section "Measurement errors estimation").
The asymptotic variance-covariance matrix of vec( ) and its estimate are given, respectively, by (the proof is in the Appendix)
) and its estimate are given, respectively, by (the proof is in the Appendix)

and

where I q denotes the q × q identity matrix and

Notice that, in the absence of measurement error, i.e.,  the corrected OLS is exactly equal to standard OLS. Furthermore, it is noteworthy that this asymptotic variance is similar to the one presented by [23] but in a multivariate manner with no correlation in the errors.
the corrected OLS is exactly equal to standard OLS. Furthermore, it is noteworthy that this asymptotic variance is similar to the one presented by [23] but in a multivariate manner with no correlation in the errors.
Hypothesis testing
Similar to the OLS with no measurement error, the interest in a simple regression model (y
i
= α + β x
i
+ ε
i
) lies in testing the strength of the relationship between the predictor gene x and the response gene y. The asymptotic distribution of vec( ) is given by
) is given by

and the test is similar to the previous case (standard OLS) described by:

This test may be performed using the Wald-type statistic expressed as

where C is a matrix of contrasts. Under the null hypothesis, (33) follows a χ2 distribution with rank(C) degrees of freedom.
Vector autoregressive model
Here we define the usual VAR model as defined in Lütkepohl (2006) [28].
Let z t = (z1t,..., z pt )⊤ be a (p × 1) vector of time series variables. The usual VAR(r) model (of order r) has the form

where n is the time series length, β j for j = 1,..., p are (p × p) coefficient matrices and ε t is an (p × 1) unobservable zero mean white noise vector process with covariance matrix Σ ε . Under stationarity conditions, the mean and autocovariance function are given, respectively, by


and

where I p denotes the p × p identity matrix.
The model (34) can be re-written as

where β = (β1β2... β
r
) is a p × pr matrix and  .
.
Therefore, if the white noise (ε) has normal distribution, the conditional Maximum Likelihood (ML) estimators of α, β and Σ ε are equal to the OLS estimators. They are given, respectively by


and

where




and

The consistence of those conditional ML estimators is assured under the stationary conditions [28]. The covariance function of  is given by
is given by

Vector autoregressive model with measurement error
Now, the VAR model with measurement error will be presented.
Let z t be the "true" variables that are not directly observed. Let Z t be the observed surrogate variables which have an additive structure given by

where Z t = (Z1t, Z2t,..., Z pt )⊤ is the surrogate vector and ϵ t = (ϵ1t, ϵ2t,..., ϵ pt )⊤ is the measurement error vector. In most cases, if the usual conditional ML estimator is adopted for the observations subject to errors, i.e., replacing z t with Z t in the equation (34), the estimator of β will be biased as well as its asymptotic variance. Therefore, in order to overcome this limitation the measurement errors should be included in the estimation procedure. Nevertheless, the model (34) plus the equation (48) is not identifiable, since the covariance matrices of ε t and ϵ t are confounded. This problem can be avoided considering known the variance of ϵ t .
Let ϵ t ~ N (0, Σϵ) be the measurement error with Σϵ known (refer to section Measurement error estimation for details about how to estimate Σϵ). Then, the parameters of the model (34) under measurement errors as in (48) have consistent estimators (Patriota et al.: Vector autoregressive models with measurement errors for testing Granger causality, submitted) given by


and

where



Then, the asymptotic distribution of vec( ) is given by [29]
) is given by [29]

where the matrix  is given by
is given by

where

where Σ v = Σ ε + Σϵ + β(I r ⊗ Σϵ)β⊤ and J l is a (r × r) matrix of zeros with one's in the |l|thdiagonal above (below) the main diagonal if l > 0 (l < 0) and J0 is a (r × r) matrix of zeros.
Notice that, if r = 1 we have the VAR(1) model and the asymptotic covariance simplifies to

where

The ithelement of vec( ), is asymptotically normally distributed with standard error given by the square root of ithdiagonal element of
), is asymptotically normally distributed with standard error given by the square root of ithdiagonal element of  . Thus, we can construct hypotheses testing on the individual coefficients, or in more general form of contrasts
. Thus, we can construct hypotheses testing on the individual coefficients, or in more general form of contrasts

involving coefficients across different equations of the VAR model. It may be tested using the Wald statistic conveniently expressed as

where C is a matrix of contrasts (C = I, for instance) and m is usually a (p × 1) vector or zeros.
Under the null hypothesis, (59) has a limiting χ2(d) distribution where d = rank(C) gives the number of linear restrictions. This test is useful to identify, in a statistical sense (controlling the rate of false positives), which gene (predictor variable) is Granger causing another gene (response variable).
Measurement error estimation
Here, two methods to estimate measurement error are proposed. One when technical replicates are available and another one in the case when they are not available.
Technical replicates
When technical replicates are available, measurement error estimation may be performed by applying a strategy extending the methods described by Dahlberg (1940) [30] (more details about Dahlberg's method in the Appendix). For microarray data, it is known that the variance varies along the spots (heteroscedasticity) due to variations in experimental conditions (efficiency of dye incorporation, washing process, etc) [31]. Moreover, it is known that Dahlberg's approach is not suitable in the presence of systematic errors. Therefore, the application of the Dahlberg's formula is not straightforward. In order to overcome this problem, we suggest the following algorithm [32].
Let W and W' be two microarrays, where W' is the technical replicate of W.
-
1.
Perform a non-linear regression such as splines smoothing between log(W) and log(W'), i.e., log(W') = f(log(W)) + ε1. Notice that the logarithm was calculated as a variance stabilizer (due to the high variance observed in microarray data). This is a common practice in microarray analysis;
-
2.
Apply again the splines smoothing between
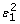 and log(W), i.e.,
and log(W), i.e., 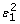 = g(log(W)) + ε2;
= g(log(W)) + ε2; -
3.
Calculate
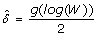 . This is a possible estimate for the standard deviation of the measurement error. Notice that with this process, we obtain one
. This is a possible estimate for the standard deviation of the measurement error. Notice that with this process, we obtain one  for each spot i = 1,..., m, where m is the number of spots in the microarray, also in the presence of heteroscedasticity.
for each spot i = 1,..., m, where m is the number of spots in the microarray, also in the presence of heteroscedasticity.
No technical replicates
However, unfortunately, technical replicates is not always available. To this case, we have developed a strategy based on negative control probes and housekeeping genes frequently provided in commercial microarrays. Technically, housekeeping genes and negative controls should not change their expression levels [33]. Therefore, any variation measured by them can be understood as measurement error. In order to overcome the problem of heteroscedasticity in microarrays, we present a method based on splines smoothing. The main idea of this method consists in estimating how much of the total variance (intrinsic biological variation + measurement error) is due to measurement error. The method is as follows:
-
1.
Let S be the set of all probes in the microarray and H be the set of housekeeping genes and negative controls. Calculate the mean and variance for each probe of S and H;
-
2.
Perform a splines smoothing in both sets of probes separately, i.e., a splines smoothing var(H) = f(mean(H)) + ε1 and var(S\{H}) = g(mean(S\{H})) + ε2, where H is a matrix containing the expression values of each housekeeping gene and negative controls in each row and S\{H} is a matrix containing the expression values of the remaining set of probes in each row. The functions f and g may be represented by a linear combination of spline functions ϕ j (·), i.e., they may be written as
 (60)
(60)
where d is the number of knots used in the spline expansion (d may be obtained by selecting the value that minimizes the Generalized Cross Validation). mean(H) and var(H) (or mean(S\{H}) and var(S\{H})) are vectors containing the mean and variance values of each row of H (or S\{H}), respectively. In this step, the smoothed curves 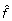 and
and  represent the estimated variance for each probe. Notice that the smoothed curve in housekeeping genes and negative controls
represent the estimated variance for each probe. Notice that the smoothed curve in housekeeping genes and negative controls 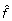 represents the estimated measurement error for each gene expression level. Moreover, the smoothed curve in the remaining set of probes
represents the estimated measurement error for each gene expression level. Moreover, the smoothed curve in the remaining set of probes  represents the total variance (intrinsic biological variance + measurement error) for each gene expression level;
represents the total variance (intrinsic biological variance + measurement error) for each gene expression level;
-
3.
Divide the smoothed curve
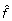 (obtained in step 2) by the other smoothed curve
(obtained in step 2) by the other smoothed curve  . Notice that this ratio (
. Notice that this ratio ( ) is the estimation of measurement error in percentage of the total variance for each probe. With this percentage, it is possible to estimate the variance of the measurement error for each probe.
) is the estimation of measurement error in percentage of the total variance for each probe. With this percentage, it is possible to estimate the variance of the measurement error for each probe.
Simulations
In order to evaluate the behavior of both, standard and proposed methods, we have conducted two simulations in small, moderate and large samples sizes (50, 100, 200 and 400). Computations were performed on the R software (a free software environment for statistical computing and graphics) [34]. For each group of simulation, 10,000 Monte Carlo samples were generated. Simulation I is for independent data and Simulation II for time series data.
Simulation I - independent data
In order to evaluate the performance of both, usual and corrected OLS methods, a controlled structure was defined. Let x and y be gene expression values where one is interested in examining if a certain gene x i (i = 1,..., p; p = 9) is linearly correlated to gene y (q = 1) partialized by other genes. This situation can be represented by the following structure

where

The observed variables X i (i = 1,...,9) and Y are defined by

where x
i
~ N(0, 1), ε ~ N (0, Σ
ε
) is the intrinsic biological random variation and ϵ1 ~ N(0,  ) independent of ϵ2 ~ N(0,
) independent of ϵ2 ~ N(0,  ) are the measurement errors, with
) are the measurement errors, with  =
=  varying from 0 to 0.8. The standard deviation Σ
ε
is defined by
varying from 0 to 0.8. The standard deviation Σ
ε
is defined by

In order to become the simulation more realistic (since actual biological gene expression signals are generally quite correlated), notice that Σ ε is not a diagonal matrix, i.e., there are little correlations between the predictors. The sample's size varied from 50 to 400.
Simulation II - time series data
In the time series case, the data has some peculiarities which are not present in the independent data. Time series data are known to be autocorrelated (past values associated with future values) and also contemporaneously correlated (contemporaneous correlation between time series). Considering these characteristics, a similar structure described in the previous section was designed. Let X t and Y t being gene expression time series data and one is interested in verifying if certain gene xi, t(i = 1,..., p; p = 9) Granger causes gene y t (q = 1). This problem can be modeled by a VAR process of order one as described below:

where

and

The observed variables X t and Y t are defined by

where ε ~ N(0, Σ
ε
) is the intrinsic biological random variation and ϵ1 ~ N(0,  ) independent of ϵ2 ~ N(0,
) independent of ϵ2 ~ N(0,  ) are the measurement errors, where
) are the measurement errors, where  varies from 0 to 0.8. The standard deviation Σ
ε
is defined by
varies from 0 to 0.8. The standard deviation Σ
ε
is defined by

The time series length varied from 50 to 400.
Notice that β0 is the autoregressive coefficient and all time series X i for i = 1,...,9 are autocorrelated and also contemporaneously correlated (Σ ε is not a diagonal matrix).
Actual biological data
The standard and proposed OLS methods were applied to lung cancer gene expression data collected by [35]. This dataset is composed of 400 microarrays, each of which constructed using a different cDNA obtained from a different patient. Standard and corrected VAR approaches were applied to mouse liver time series data collected by [36]. This data is composed by 48 time points distributed at intervals of 1 hour.
Appendix
Proof of the asymptotic variance of β- equation (29)
Here, we proof equation (29), i.e., the asymptotic variance of β in the multivariate case with no correlated errors.
Consider the following model:

where X i and Y i are the observed vectors with dimensions p × 1 and q × 1, respectively, α is the model intercept (q × 1), β is a (q × p) matrix of slope parameters, ε i is a white noise vector with mean zero and covariance matrix Σ ε . The joint distribution of ϵ1i, ϵ2i, ε i and x i is given by

In this section, we investigate the asymptotic distribution of

where

and

The proof idea, similar to presented in [23], has two main steps. The first step consists in showing that vec( ) - vec(β⊤) can be written as linear combinations of a vectorial mean. In the second one, we must demonstrate that this vectorial mean has an asymptotic normal distribution. Therefore, we need some auxiliar results for proving the asymptotic result, which are exposed in two propositions below.
) - vec(β⊤) can be written as linear combinations of a vectorial mean. In the second one, we must demonstrate that this vectorial mean has an asymptotic normal distribution. Therefore, we need some auxiliar results for proving the asymptotic result, which are exposed in two propositions below.
Proposition 1 Under the model (61) under (62) the proposed estimator  has the following relationship
has the following relationship

where

with W
i
= (ε
i
+ ϵ2i- β ϵ1i) ⊗ (x
i
- μ
x
+ ϵ1i) - Ψ, Ψ = (I
q
⊗  )vec(β⊤) and b
n
=
)vec(β⊤) and b
n
=  means that nb
n
is limited in probability when n diverges. It implies that,
means that nb
n
is limited in probability when n diverges. It implies that,  prob
(n-1) goes to zero when n increases.
prob
(n-1) goes to zero when n increases.
Proof: Define β k as the coefficients associated with the kthelement of the vector y i , that is

Thus, we have that vec(β⊤) = ( )⊤ and its estimator can be written as
)⊤ and its estimator can be written as  , where
, where  and
and  for k = 1,..., q. Moreover, the model (61) may be rewritten in terms of the observed variables as
for k = 1,..., q. Moreover, the model (61) may be rewritten in terms of the observed variables as

and for the kthelement of Y i we have

where ϵ2i= (ϵ2,1i,...,ϵ2, qi)⊤.
Then, it follows that

where  . Thus, denoting
. Thus, denoting  we have that
we have that

with  . As a result, we have
. As a result, we have

where  and W
ki
= (x
i
- μ
x
+ ϵ1i)ϑ
ki
- Ψ
k
. Hence, it follows that
and W
ki
= (x
i
- μ
x
+ ϵ1i)ϑ
ki
- Ψ
k
. Hence, it follows that

where

with W
i
= (ε
i
+ ϵ2i- β ϵ1i) ⊗ (x
i
- μ
x
+ ϵ1i) - Ψ and Ψ = (I
q
⊗  ) vec(β⊤).
) vec(β⊤).
Proposition 2 Under all conditions stated in this paper, the mean  of Proposition has an asymptotic distribution given by
of Proposition has an asymptotic distribution given by

where  means "converge in distribution to",
means "converge in distribution to",

and 
Proof: Notice that the expectation of W
i
is equal to zero for all i. Then, defining  , where x
i
= δ⊤W
i
we have that E(x
i
) = 0, Var(x
i
) = δ⊤E(W
i
, where x
i
= δ⊤W
i
we have that E(x
i
) = 0, Var(x
i
) = δ⊤E(W
i
 )δ and
)δ and

with F i = (ε i + ϵ2i- β ϵ1i) (ε i + ϵ2i- β ϵ1i)⊤. Thus, using the fact that the random quantities have independent normal distributions and we have that

That is, x1..., x n is an iid sequence and we can use the central limit theory, which says that

where V = δ⊤ T δ with  . As
. As  is asymptotically normally distributed for all δ ≠ 0
r
then, by the Cramer-Wold device [37], we have that
is asymptotically normally distributed for all δ ≠ 0
r
then, by the Cramer-Wold device [37], we have that

Then, by the Propositions (1) and (2), we have that

where  .
.
Dahlberg's error
Consider the following model:

where Z ij is the measure obtained in one experiment (microarray), i is the sample index i = 1,..., m, m is the number of spost in the microarray, j is the replicate number (j = 1, 2 in the case of duplicates), μ i is the unknown true value of the measure and ϵ ij is the error of measure.
Then, assume that E(ϵ
ij
) = 0 and Var(ϵ
ij
) =  . Thus, one quantification of the quality of measure is the standard deviation of ϵ
ij
, i.e., δϵ. Notice that the lower is the standard deviation of the error of measure (δϵ), the lower is the measurement error.
. Thus, one quantification of the quality of measure is the standard deviation of ϵ
ij
, i.e., δϵ. Notice that the lower is the standard deviation of the error of measure (δϵ), the lower is the measurement error.
Consider

Therefore

Assuming that there is no bias (systematic error), one intuitive estimator for  is
is

The quantity  is exactly the Dahlberg's formula proposed in [30].
is exactly the Dahlberg's formula proposed in [30].
References
Mar JC, Kimura Y, Schroder K, Irvine KM, Hayashizaki Y, Suzuki H, Hume D, Quackenbush J: Data-driven normalization strategies for high-throughput quantitative RT-PCR. BMC Bioinformatics 2009, 10: 110. 10.1186/1471-2105-10-110
Fontaine L, Even S, Soucaille P, Lindley ND, Cocaign-Bousquet M: Transcript quantification based on chemical labeling of RNA associated with fluorescent detection. Anal Biochem 2001, 298(2):246–52. 10.1006/abio.2001.5390
Yuk FL, Cavalieri D: Fundamentals of cDNA microarray data analysis. Trends in Genetics 2003, 19: 649–659. 10.1016/j.tig.2003.09.015
Yang YH, Buckley MJ, Dudoit S, Speed TP: Comparison of methos for image analysis on cDNA microarray data. Journal of Computational and Graphical Statistics 2002, 11: 108–136. 10.1198/106186002317375640
Karakacj TK, Wentzell PD: Methods for estimating and mitigating errors in spotted, dual-coloer DNA microarrays. OMICS 2007, 11(2):186–99. 10.1089/omi.2007.0008
Kim K, Page GP, Beasley TM, Barnes S, Scheirer KE, Allison DB: A proposed metric for assessing the measurement quality of individual microarrays. BMC Bioinformatics 2006., 7(35):
Strimmer K: Modeling gene expression measurement error: a quasi-likelihood approach. BMC Bioinformatics 2003., 4(10):
Liu X, Milo M, Lawrence ND, Rattray M: Probe-level measurement error improves accuracy in detecting differential gene expression. Bioinformatics 2006, 22(17):2107–13. 10.1093/bioinformatics/btl361
Zhang D, Wells MT, Smart CD, Fry WE: Bayesian normalization and identification for differential gene expression data. Journal of Computational Biology 2005, 12: 391–406. 10.1089/cmb.2005.12.391
Dojer N, Gambim A, Mizera A, Wilczński B, Tiuryn J: Applying dynamic Bayesian networks to perturbed gene expression data. BMC Bioinformatics 2006, 7: 249. 10.1186/1471-2105-7-249
Friedman N, Linial M, Nachman I, Pe'er D: Using Bayesian networks to analyze expression data. Journal of Computational Biology 2000, 7: 601–620. 10.1089/106652700750050961
Akutsu T, Miyano S, Kuhara S: Algorithms for identifying Boolean networks and related biological networks based on matrix multiplication and fingerprint function. Journal of Computational Biology 2000, 7: 331–343. 10.1089/106652700750050817
Pal R, Datta A, Bittner M, Dougherty E: Intervention in context sensitive probabilistic Boolean networks. Bioinformatics 2005, 21: 1211–1218. 10.1093/bioinformatics/bti131
Moriyama M, Hoshida Y, Otsuka M, Nishimura S, Kato N, Goto T, Taniguchi H, Shiratori Y, Seki N, Omata M: Relevance network between chemosensitivity and transcriptome in human hepatoma cells. Molecular Cancer Therapeutics 2003, 2: 199–205.
Shchäffier J, Strimmer K: An empirical Bayes approach to inferring large-scale gene association networks. Bioinformatics 2005, 21: 754–764.
Chen KC, Wang TY, Tseng HH, Huang CYF, K CY: A stochastic differential equation model for quantifying transcriptional regulatory network in Saccharomyces cerevisiae. Bioinformatics 2005, 21(12):2283–2890.
Fujita A, Sato J, Demasi M, Sogayar M, Ferreira C, miyano S: Comparing Pearson, Spearman and Hoeffding's D measure for gene expression association analysis. Journal of Bioinformatics and Computational Biology 2009, 7(4):663–684. 10.1142/S0219720009004230
Shimamura T, Imoto S, Yamaguchi R, Fujita A, Nagasaki M, miyano S: Recursive regularization for inferring gene networks from time-course gene expression profiles. BMC Systems Biology 2009., 3(41):
Mukhopadhyay ND, Chatterjee S: Causality and pathway search in microarray time series experiment. Bioinformatics 2007, 23: 442–449. 10.1093/bioinformatics/btl598
Fujita A, Sato J, Garay-Malpartida H, Morettin P, Sogayar M, Ferreira C: Time-varying modeling of gene expression regulatory networks using the wavelet dynamic vector autoregressive method. Bioinformatics 2007, 23(13):1623–1630. 10.1093/bioinformatics/btm151
Fujita A, Sato J, Yamaguchi Garay-MalpartidaR, Miyano S, Sogayar M, Ferreira C: Modeling gene expression regulatory networks with the sparse vector autoregressive model. BMC Systems Biology 2007, 1: 39. 10.1186/1752-0509-1-39
Fujita A, Sato J, Garay-Malpartida H, Sogayar M, Ferreira C, Miyano S: Modeling nonlinear gene regulatory networks from time series gene expression data. Journal of Bioinformatics and Computational Biology 2008, 6(5):961–979. 10.1142/S0219720008003746
Fuller W: Measurement error models. New York: Wiley; 1987.
Edery I: Circadian rhythms in a nutshell. Physiol Genomics 2000, 3(2):59–74.
Patriota AG, Bolfarine H, Castro M: A heteroscedastic structural errors-in-variables model with equation error. Statistical Methodology 2009, 6(4):408–423. 10.1016/j.stamet.2009.02.003
Wille A, Zimmermann P, Vranová E, Fürholz A, Laule O, Bleuler S, Hennig L, Prelić A, von Rohr P, Thiele L, Zitzler E, Gruissem W, Bühlmann P: Sparse graphical Gaussian modeling of the isoprenoid gene network in Arabidopsis thaliana . Genome Biology 2004, 5: r92. 10.1186/gb-2004-5-11-r92
Graybill F: Theory and application of the linear model. Massachusetts: Duxubury Press; 1976.
Lütkepohl H: New introduction to multiple time series analysis. Berlin: Springer; 2006.
Patriota AG, Sato JR, Blas BG: Vector autoregressive models with measurement errors for testing Granger causality. arXiv:0911.5628v1 arXiv:0911.5628v1
Dahlberg G: Statistical methods for medical and biological students. New York: Interscience Publications; 1940.
Fan J, Tam P, Woude GV, Ren Y: Normalization and analysis of cDNA microarrays using within-array replications applied to neuroblastoma cell response to a cytokine. PNAS 2004, 101(5):1135–1140. 10.1073/pnas.0307557100
Fujita A, Sato J, da Silva F, Galvão M, Sogayar M, Miyano S: Quality control and reproducibility in DNA microarray experiments. Genome Informatics, in press.
Eisenberg E, Levanon EY: Human housekeeping genes are compact. Trends in Genetics 2003, 19(7):362–365. 10.1016/S0168-9525(03)00140-9
The R Project for Statistical Computing[http://www.r-project.org/]
Director's Challenge Consortium for the Molecular Classification of Lung Adenocarcinoma S Shedden, Taylor JMG, Enkemann SA, Tsao MS, Yeatman TJ, Gerald WL, Eschrich S, Jurisica I, Giordano TJ, Misek DE, Chang AC, Zhu CQ, Strumpf D, Hanash S, Shepherd FA, Ding K, Seymour L, Naoki K, Pennell N, Weir B, Verhaak R, Ladd-Acosta C, Golub T, Gruid M, Sharma A, Szoke J, Zakowski M, Rusch V, Kris M, Viale A, Motoi N, Travis W, Conley B, Seshan VE, Meyerson M, Kuick R, Dobbin KK, Lively T, Jacobson JW, Beer DG: Gene expression based survival prediction in lung adenocarcinoma: a multi-site, blinded validation study. Nature Medicine 2008, 14: 822–827. 10.1038/nm.1790
Hughes ME, DiTacchio L, Hayes KR, Vollmers C, Pulivarthy S, Baggs JE, Panda S, Hogenesch JB: Harmonics of circadian gene transcription in mammals. PLoS Genetics 2009, 5(4):e1000442. 10.1371/journal.pgen.1000442
Athreya K, Lahiri S: Measure theory and probability theory. Berlin: Springer; 2006.
Acknowledgements
This research was supported by grants from RIKEN and FAPESP.
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
AF has made substantial contributions to the conception, design and implementation of the study, and has also been responsible for drafting the manuscript. AGP has made substantial contributions to the development of the methods. JRS has made contributions to data analysis. SM has discussed the results and critically revised the manuscript. All authors read and approved the final version of the manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fujita, A., Patriota, A.G., Sato, J.R. et al. The impact of measurement errors in the identification of regulatory networks. BMC Bioinformatics 10, 412 (2009). https://doi.org/10.1186/1471-2105-10-412
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2105-10-412




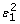 and log(W), i.e.,
and log(W), i.e., 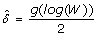 . This is a possible estimate for the standard deviation of the measurement error. Notice that with this process, we obtain one
. This is a possible estimate for the standard deviation of the measurement error. Notice that with this process, we obtain one  for each spot i = 1,..., m, where m is the number of spots in the microarray, also in the presence of heteroscedasticity.
for each spot i = 1,..., m, where m is the number of spots in the microarray, also in the presence of heteroscedasticity.
 ) is the estimation of measurement error in percentage of the total variance for each probe. With this percentage, it is possible to estimate the variance of the measurement error for each probe.
) is the estimation of measurement error in percentage of the total variance for each probe. With this percentage, it is possible to estimate the variance of the measurement error for each probe.