- Methodology article
- Open access
- Published:
Novel domain expansion methods to improve the computational efficiency of the Chemical Master Equation solution for large biological networks
BMC Bioinformatics volume 21, Article number: 515 (2020)
Abstract
Background
Numerical solutions of the chemical master equation (CME) are important for understanding the stochasticity of biochemical systems. However, solving CMEs is a formidable task. This task is complicated due to the nonlinear nature of the reactions and the size of the networks which result in different realizations. Most importantly, the exponential growth of the size of the state-space, with respect to the number of different species in the system makes this a challenging assignment. When the biochemical system has a large number of variables, the CME solution becomes intractable. We introduce the intelligent state projection (ISP) method to use in the stochastic analysis of these systems. For any biochemical reaction network, it is important to capture more than one moment: this allows one to describe the system’s dynamic behaviour. ISP is based on a state-space search and the data structure standards of artificial intelligence (AI). It can be used to explore and update the states of a biochemical system. To support the expansion in ISP, we also develop a Bayesian likelihood node projection (BLNP) function to predict the likelihood of the states.
Results
To demonstrate the acceptability and effectiveness of our method, we apply the ISP method to several biological models discussed in prior literature. The results of our computational experiments reveal that the ISP method is effective both in terms of the speed and accuracy of the expansion, and the accuracy of the solution. This method also provides a better understanding of the state-space of the system in terms of blueprint patterns.
Conclusions
The ISP is the de-novo method which addresses both accuracy and performance problems for CME solutions. It systematically expands the projection space based on predefined inputs. This ensures accuracy in the approximation and an exact analytical solution for the time of interest. The ISP was more effective both in predicting the behavior of the state-space of the system and in performance management, which is a vital step towards modeling large biochemical systems.
Background
In systems biology, it is crucial to understand the dynamics of large and complicated biochemical reaction networks. Recent advances in computing and mathematical techniques mean it is easier for biologists to deal with enormous amounts of experimental data, right down to the level of a single molecule of a species. Such information reveals the presence of a high level of stochasticity in the networks of biochemical reactions. In biochemical reaction networks, stochastic models have made significant contributions to the fields of systems biology [1, 2], neuroscience [3], and drug modeling [4].
In a complex system, biochemical reactions are often modeled as reaction rate equations (RREs) using ordinary differential equations (ODEs). Examples of this kind of work include the biochemical networks of Alzheimer's disease (AD) [5]; the pathways in the fungal pathogen Candida albicans [6]; and the COVID-19 coronavirus pathogen network [7]. In each of these examples, the behavior of different pathways is still largely unknown. All these models only contain species with small copy numbers and widely different reaction rates; the probabilistic descriptions of time evolution of molecular concentrations (or numbers) are more suited for understanding the dynamics of such systems. One probabilistic approach for modeling a biochemical reaction network is to deduce a set of integro-differential equations known as chemical master equations (CMEs) [8, 9]. CMEs describe the evolution of the probability distribution over the entire state-space of a biochemical system that jumps from one set of states to another set of states in continuous time: they are a continuous time version of Markov chains (CTMCs) [8, 10] with discrete states. By defining the Markov chain [10, 11], we can consider the joint and marginal probability densities of the species in a system that changes over time [12].
In such cases, the development of RREs with molecular numbers becomes very important. The biochemical reaction network can be defined in terms of the discrete state\( X\equiv {\left({x}_1,\dots, {x}_{\widetilde{\mathrm{N}}}\right)}^T \) vector of non-negative integers \( {x}_{\widetilde{\mathrm{N}}} \) for the given conditions, where \( \widetilde{\mathrm{N}} \) ≥1. {X(t) : t ∈ K; φ} defines a stochastic process, where K is the indexing scheme and φ is the sample space. Following the derivation in [9], for every reaction, there exists a reaction channel, RM, which determines the unique reaction in the system with a propensity function kM. The specific combinations of the reactant species in RM will react during an infinitesimal [t, t + dt) time interval. The average probability aμ(X(t))dt of a particular RM fires within [t, t + dt) is the multiplication of the numbers of reactant species, denoted by square brackets, by kM. For example,
In the case where the reactants are of the same type, for example \( A+A\overset{k_2}{\to }\ T \), then \( {a}_2:{k}_2\left(\frac{\left[A\right]\left[\left(A-1\right)\right]}{2}\right) \). The set consisting of all the reaction channels, RM, is the union of sets of fast reactions and slow reactions [12]. They are categorized into sets of RM(fs) and RM(sr) reactions, respectively, based on their propensity values. Therefore,
A reaction is faster than others if its propensity is of several orders of magnitude larger than the other propensity values (see the list of abbreviations and notations at the end).
Chemical master equation
In this paper, we consider a network of biochemical reactions at a constant volume. The network consists of \( \widetilde{\mathrm{N}} \) ≥1 different species \( \left\{{S}_1,\dots {S}_{\widetilde{\mathrm{N}}}\right\} \). They are spatially homogeneous and interact through M ≥1 reaction channels in thermal equilibrium. The number of counts of each different species defines the state of the system. If all the species are bounded by S, then the approximate number of states in the system would be \( {S}^{\widetilde{\mathrm{N}}} \) [13]. Each state \( X\equiv {\left({x}_1,\dots {x}_{\widetilde{\mathrm{N}}}\right)}^T \). \( {x}_{\widetilde{\mathrm{N}}} \), denotes the number of molecules (counts) of each species. For every state, X, the probability satisfies the following CME [8],
where P(t)(X) = the probability function, representing the time-evolution of the system, given that t ≥ t0 and the initial probability is, \( {P}^{\left({t}_0\right)}\left({X}_0\right) \),
M = elementary chemical reaction channels R1, … .. RM,
aμ = chemical reaction propensity of channel μ = {1, 2, …. M}, and
vμ = the stoichiometric vector that represents a change in the molecular population of the chemical species due to the occurrence of one RM reaction. The system transitions to a new state: X + vμ records the changes in the number of counts of different species when the reactions occur.
We note that aμ(X − vμ)dt is the probability for state (X − vμ) to transition to state X through chemical reaction, RM, during [t, t + dt), and \( {\sum}_{\mu =1}^M{a}_{\mu }(X) dt \) is the probability for the system to shift from state X as a result of any reaction during dt. If \( {\mathbf{X}}_J=\left\{{X}_1,\dots \dots .{X}_{S^{\widetilde{\mathrm{N}}}}\right\} \) is the ordered set of possible states of the system indexed by {1, 2…K} having \( {S}^{\widetilde{\mathrm{N}}} \) elements, then Eq. (2) represents the set of ordinary differential equations (ODEs) that determines the changes in probability density P(t)= (P(t)(X1), … \( {P}^{(t)}\left({X}_{S^{\widetilde{\mathrm{N}}}}\right)\Big){}^T \). Once XJ is selected, the matrix-vector form of Eq. (2) is described by an ODE:
where the transition rate matrix is A = [ai,j]. If each reaction leads to a different state, \( {X}_{i^{\prime }} \), then the elements in submatrix Ai,j are given as:
This equation represents the infinitesimal generator of the Markov process [10, 14, 15]. Rows and columns are ordered in lowercase letters, i and j respectively. The entry of ai,j of the matrix determines the propensity for the chemical system to transition from one state to another state, given that i ≠ j, are non-negative. The diagonal terms of the matrix are defined by ajj, when i = j and the matrix has a zero-column sum, so its probability is conserved. From Eq. (3) we can derive the \( {P}^{\left({t}_f\right)} \) probability vector at the final time, tf, of interest given an initial density of \( {P}^{\left({t}_0\right)} \):
where the matrix exponential function is defined by the convergent Taylor series as [16, 17]
However, algorithms, such as in [13, 18,19,20] truncate Eq. (6) infinite summation to approximate Eq. (3) at the cost of a truncation error.
Initial value problem
If vμ or vM, for μ or M = {1, 2, …. M} are the stoichiometric vectors for RM reaction channels, then we will define the stoichiometric matrix for the system by Vμ or VM = [v1; v2; ……vμ]T. If φ is the sample space and X0 ∈ φ is the initial state of the system, XJ denotes the only set of states in φ. To solve P(t)(X) in Eq. (2) for X ∈ φ, we define the P(t) vector as(P(t)(X))X ∈ φ or \( {\left({P}^{(t)}(X)\right)}_{X\in {\mathbf{X}}_J} \) for a finite set of states, then \( \frac{\partial {P}^{(t)}}{\partial t} \) is defined as a vector \( {\left(\frac{\partial {P}^{(t)}}{\partial t}\right)}_{X\in \upvarphi} \). Solving the CME involves finding the solution of the initial value problem over a time period using the differential equation Eq. (3) when t > 0, whereas, \( {P}^{\left({t}_0\right)} \) is the initial distribution at t = 0. Here, the sample space φ can be infinite for large biochemical systems. Finding the solution for Eq. (3) for the given parameters with a finite set of states XJ is a major problem for CME’s because in large biochemical systems the size of A will be extremely large.
For example, consider an enzymatic reaction network [13] described by reactions \( {R}_1:S+E\overset{k_1}{\to }\ C \), \( {R}_2:C\overset{k_2}{\to }\ S+E \), \( {R}_3:C\ \overset{k_3}{\to }\ P+E \). This network of reactions involves four species: namely, S− substrate, E− enzyme, C− complex and P− product molecules. The X ≡ (x1, x2, x3, x4)T ≡ (S, E, C, P)T represents any state of the system, with X0 ≡ (S0, E0, C0, P0) given as the initial state. The stoichiometric vectors are given by v1 = (−1, −1, 1, 0), v2 = (1, 1, −1, 0), v3 = (0, 1, −1, 1). Therefore, for (x1, x2, x3, x4) \( {x}_{\widetilde{\mathrm{N}}=4} \), the propensity functions are:
The set of states reachable from X0 is finite in number. With multiple explosions of the number of states in a large model, the size of A increases exponentially.
As seen in Eq. (5), solving Eq. (2) becomes a problem when the model’s dimensions grow due to the increase of species present in the system. This is particularly true for large biochemical models. The approximate estimate of \( {S}^{\widetilde{N}} \) shows how the size of the problem increases. This explosion in size is known as the curse of dimensionality [9, 13]. The CME solution given in Eq. (5) has two major parts: (a) the expansion of the state-space, and (b) the approximation of the series. For the expansion of state-space, Finite State Projection (FSP) [21] and Sliding Windows (SW) [18] are used to find the domain. Methods like Krylov subspace [13] and Runge Kutta [22] are commonly used for approximation (of the series) of the CME Eq. (5).
Although CME has been employed and solved explicitly for relatively small biological systems [13, 18,19,20, 23, 24], computationally complaisant but accurate solutions are still unknown for most significant systems and for large systems which have an infinite (or a very large) number of states. This lack of closed-form solutions has driven the system biology research towards Monte-carlo Algorithms (MC) [25] to capture dynamics. One algorithm, the Stochastic Simulation Algorithm (SSA) by Gillespie [9], has been used in the CME. Although the original FSP state-space expansion has been used in research [21, 26], it has some drawbacks [21]. The FSP [21] and its variants [20, 24, 26, 27] are based on r-step reachability [26]. While SW [18] is also a FSP based method, it employs a stochastic simulation algorithm (SSA) to find the domain. This is more effective than FSP and suitable for stiff problems. Add-on weighting functions like GORDE [28] and likelihoods [24] methods are used to improve the expansion. FSP GORDE [28] removes the states with small probabilities before the calculation of Eq. (5). This practice saves computational time, meaning that FSP GORDE performs faster than conventional FSP r-step reachability. However, removing the probabilities before the calculation of Eq. (5) increases the steps error and affects the accuracy of the final solution at tf regardless of whether the state-space is small or large. If one is interested in solving stiff and/or large systems, it will greatly affect the solution.
The FSP variant, Optimal Finite State Projection (OFSP), [20] based on r-step reachability, performs better in terms of producing optimal order domain. It is faster than both FSP and FSP GORDE. However, it is infeasible to use SW for large CME problems because creating hyper-rectangles is a very difficult task. At least four-times the number of SSA simulations are required to minimize the error by half, because of very low convergence rates of routines in MC . The original SSA takes a long time, because one simulation may have several different RM. Recently, the SSA’s efficiency has been greatly enhanced by researchers through various schemes such as τ leaps (adaptive) [29, 30]. Thus, we compare the OFSP and SSA (τ leaps adaptive) against the ISP in terms of finding the domain, accuracy and computational efficiency. Key to solving the CME remains in finding the right projection size (domain) for large models which would then ensure efficient approximation.
In this paper, we focus primarily on developing the expansion strategy, namely the Intelligent State Projection (ISP) method, to mitigate several problems: the accuracy of the solution, the performance of the method and projection size. The ISP has two variants: the Latitudinal Search (LAS) and the Longitudinal-Latitudinal Search (LOLAS). It treats the Markov chain of a biochemical system as a Markov chain tree structure and states as objects of class node. Based on the dimension of the system, search is performed in a latitudinal way for different model sizes using the ISP LAS method. Whereas, bidirectional search is applied using ISP LOLAS, which quickly expands the state-space up to a specified bound limit. To support the expansion strategy, we also develop the Bayesian Likelihood Node Projection (BLNP) function, based on Bayes’ theorem [31, 32]. It is adjoined with the ISP variants to determine the likelihood of events at any interval at the molecular population level. BLNP provides confidence to the expansion strategy by assigning probability values to the occurrence of future reactions and prioritizing the direction of expansion. The ISP embedding BLNP function inductively expands the multiple states with the likelihood of occurrence of fast and slow reactions [12]. It also defines the complexity of the system by predicting the pattern of state-space updation, and the depth of the end state from the initial state. When used for any size of biological networks, LAS’ memory usage is proportional to the entire width of expansion; it is less than ISP LOLAS. Both methods are feasible and differentiated for various types of biological networks. However, the computational time for both variants depend on the nature of the model and the size of the time step used. At any point, the amount of memory in use is directly proportional to the neighboring states reachable through a single RM reaction. ISP LOLAS uses considerably less memory, even when it retracts to the initial node to track new reactions, then revisiting the depth many times.
Results
Having discussed the CME solution, we now discuss the modeling and integration of the biochemical reaction systems for the ISP methods, as well as the assumptions underlying these methods. Using ISP, we tested its ability to reproduce the model to measure dynamics of the key parameters in the models. The ISP method is a novel, easy-to-use, technique for modeling and expanding the state-space of biochemical systems. It features several improvements in modeling and computational efficiency.
The computational experiment (initializing and solving the model) was conducted on the carbon-neutral platform of Amazon® Web Service Elastic Computing (EC2), instance type large (m5a), running on HVM (hardware virtual environment) virtualization with variable ECUs. We used multicore environment 16vCPU @ 2.2GHz, AMD EPYC 7571 running Ubuntu 16.04.1 with relevant dependencies, and 64GB memory with 8GB Elastic Block Storage (EBS) type General Purpose SSD (GP2) formatted with Elastic File System (EFS). The performance mode was set to General Purpose with input-output per second (IOPS = 100/3000). We used the type bursting throughput mode (see Supplementary Information (SI) 1).
Intelligent state projection
The main aim of the proposed algorithm is to expand the XK iteratively, such that XK contains a minimum number of states carrying the maximum probability mass of the system. To create the sample space for ISP, a Markov chain tree Ѭ [33] was used to visualize a biochemical system to exhibit the transition matrix as directed trees [10, 11] of its associated graph. Additionally, the Markov chain tree Ѭ generates sample space of the system to represent Markov processes associated with the Markov chain and the transition matrices of biochemical reaction networks. In following section, we visualize the Markov chain of the biochemical system as a Markov chain graph (tree) for ISP compatibility.
Markov chain as a Markov chain tree
We define the Markov chain tree, Ѭ, [33] as infinite and locally finite. It is a special type of graph with a prominent vertex called a parent node without loops or cycles. If graph Gmc is a state-space of the finite state Markov chain with \( \left\{P\left({X}_i,{X}_{i^{\prime }}\right)\ \right|\ {X}_i,{X}_{i^{\prime }}\in {G}_{mc}\Big\} \) transition probabilities meeting the condition \( \sum \limits_{X_{i^{\prime }}}P\left({X}_i,{X}_{i^{\prime }}\right)=1 \), then the induced Markov chain tree is a combination of valued Gmc random variables with the distributions inductively defined from \( P\left({X}_i,{X}_{i^{\prime }}\right) \) with an initial state, Xi ∈ Gmc. That being the case, it is easy to expand this class of Markov random field through a Markov chain tree structure for biochemical systems. Furthermore the Markov chain tree and the Markov processes can be equated as explained in [34] for the stochastic analysis.
Since we are interested in aperiodic states in the expansion of state-space, we shall assume the reducibility or simplification of the Gmc; namely for each \( {X}_i,{X}_{i^{\prime }}\in {G}_{mc} \) through Ѭ. Therefore, let us concentrate on the case where Gmc is considered as a locally finite connected graph. The transition probabilities of each state are not equal due to the propensities and parameters of different reactions in the biochemical system. Consequently, a Markov chain tree, Ѭ, can be used to visualize a biochemical system process to exhibit a transition matrix as directed trees of its associated graph [10, 11]. It can also be used to generate a sample space for the system to represent the Markov processes and the transition matrices of biochemical reaction networks. We discuss the details needed to represent Markov models on trees and working with graphs for state-space later.
If XJ is the finite set of cardinality {1, 2……. K} of a Markov chain Ѫc, then A is the transition probability matrix associated with XJ. A state-space is, substantially, a class of a set of states containing the unique state of the system. The arcs between the states represent the transitions from the initial state to the end state. This transition is defined as transient and communicating class in graphs. When all the transitions are combined, every state-space takes the form of a graph and creates the state-space of the system, as shown in Fig. 1 below.
We can now associate chain Ѫc with the directed graph Gmc = (XJ, Vμ), where Vμ = [v1; v2; ……vμ]. vμ defines the transition from state Xi to \( {X}_{i^{\prime }} \) and is denoted as \( {v}_{\upmu}=\left\{\left({X}_i,{X}_{i^{\prime }}\right);{a}_{i,j}>0\right\} \). For every transition \( \left({X}_i,{X}_{i^{\prime }}\right)\in {\mathbf{X}}_J \), then weight \( \omega \left({X}_i,{X}_{i^{\prime }}\right) \) is ai, j.
Suppose Gmc has a cycle, which starts and terminates at some state, Xi ∈ XJ. If there is a transition from Xi to \( {X}_{i^{\prime }} \), we add a unique transition by creating a cycle from Xi back to itself and then consider the original transition from Xi to \( {X}_{i^{\prime }} \). This contradicts the uniqueness of the walk in tree [35]. In terms of the CTMC of a biochemical system process, the change in molecular population is defined by a stoichiometric vector, so, in Gmc, there must be at least one intermediate state that will send the system back to the previous state to create the cycle. This process categorizes the forward and backward reactions given the initial state, X0, of the system. The transient class of the transition leads the system to a unique state that defines the forward reaction in the system. In contrast, the communicating class of a transition defines the reversible reaction in the system. We define such systems as transient class systems and communicating class systems. Large biochemical systems are usually a combination of both classes.
A biochemical system is visualized as a tree Ѭ [33] to enable the expansion of the state-space. A tree, Ѭ, is a special form of graph in data structure constituting a set of nodes and a collection of edges (or arcs), each of which connects to an ordered pair of nodes. Gmc is considered a directed tree, Ѭ. It is rooted with N0 = (X0, ƌl) if it contains a unique walk to Ni = (Xi, ƌl + 1) and does not contain any cycles. Meanwhile, if Xi ∈ XJ\{X0} has exactly one outgoing transition away from X0 it is called an arborescence. If it makes its transition towards N0 = (X0, ƌl) it is called an anti-arborescence. An arborescence is a subset ⊆Vμ that has one edge out of every node that contains no cycles and has maximum cardinality. For example, if set U = {5, 7, 8, 10} contains 4 elements, then the cardinality of ∣U∣ is 4.
If Xi and \( {X}_{i^{\prime }} \)are the states other than the initial X0 state, there is a transition from Xi to \( {X}_{i^{\prime }} \), so Xi has at least one transition. Now, suppose Xi has two walks, (Xi, Xi + 1) and (Xi, Xi + 2). Concatenating these walks to the walks (Xi + 1, \( {X}_{i^{\prime }} \)) and (Xi + 2, \( {X}_{i^{\prime }} \)), respectively, we have two distinct changes in state from Xi to \( {X}_{i^{\prime }} \) in Gmc. However, in Ѭ, this concatenation is not considered, which makes them Directed Acyclic Graphs (DAG) (see Fig. 2). Most of the biochemical models Gmc can be visualized as DAGs irrespective of the nature of the reactions present in the model. Figure 2 shows the equivalent Gmctree of shown in Fig. 1. The trees are less complex as they have no cycles, no self-loops. Yet they are still connected, meaning they can depict the state-space.
Equivalent tree of a Markov chain graph, as shown in Fig. 1. This is a special form of graph which has no cycle and no self-loops. It depicts the state-space of the system in the form of a tree (DAG)
The weight of the tree containing all e edges is defined by  , where \( \omega (e)=\omega \left({X}_i,{X}_{i^{\prime }}\right)={a}_{i,j} \) is the weight of an edge starting from Xi and ending at \( {X}_{i^{\prime }} \) when
, where \( \omega (e)=\omega \left({X}_i,{X}_{i^{\prime }}\right)={a}_{i,j} \) is the weight of an edge starting from Xi and ending at \( {X}_{i^{\prime }} \) when  [36]. For systems which have both forward and backward reactions, if nJ is the total number of nodes indexed by {1, 2…K} the same as states, then nK is the set of nodes carrying XK, and \( {\mathbf{n}}_K^{\prime } \) is the set of nodes carrying \( {\mathbf{X}}_K^{\prime } \) given N0 root node of the tree Ѭ, then the walk from one node to another node is given by:
[36]. For systems which have both forward and backward reactions, if nJ is the total number of nodes indexed by {1, 2…K} the same as states, then nK is the set of nodes carrying XK, and \( {\mathbf{n}}_K^{\prime } \) is the set of nodes carrying \( {\mathbf{X}}_K^{\prime } \) given N0 root node of the tree Ѭ, then the walk from one node to another node is given by:
Ѭ is formed by superimposing the forward transitions between the states Xi and \( {X}_{i^{\prime }} \), with the reverse orientation. Where \( {X}_{i^{\prime }} \) and Xi, indicate backward reactions, these are graphically denoted as an individual edge from Ni = (Xi, ƌl) to Ni' = (Xi, ƌl + 11) to Ni = (Xi, ƌl + 2) in a tree. The Ni of ƌl + 2 can be renamed as a new node. Ni + 1, remains as it is at a different depth from the Ni of ƌl but contains the same state Xi. In the expansion, repeated states are not considered in the domain; therefore, any node which carries a similar state is considered the same, regardless of the level and indexing. Consideration of trees for the state-space expansion in ISP not only helps to reduce the complexity but also improves the accuracy of the solution of Eq. (5) by identifying nodes which carry probable states. If the Markov chain graph starts in state Xi ∈ XJ, then the mean number of transits to any state \( {X}_{i^{\prime }} \) converging to \( \overline{a_{X_i,{X}_{i^{\prime }}}} \) is given by the (i, i′)th value of
U is the set of all arborescences. Let \( {U}_{X_i,{X}_{i^{\prime }}} \) is the set of all arborescences which have a transition from Xi to \( {X}_{i^{\prime }} \) and \( \left\Vert {U}_{X_i,{X}_{i^{\prime }}}\right\Vert \) is the sum of the weights of the arborescences in \( {U}_{X_i,{X}_{i^{\prime }}} \) then according to the Markov chain tree theorem [33],
\( \overline{a_{X_i,{X}_{i^{\prime }}}} \) is probabilistic in nature. This nature is not only restricted to the systems which have irreducible Markov chains, in which graph Gmc is strongly connected while carrying probable state-spaces, but also for the systems that can be simplified by converting to a Markov chain tree and then by reducing that tree by ignoring the states which have low probabilities in space φ.
Expansion criterion for state space
As previously mentioned, the states are indexed using {1, 2……. K} in the domain denoted by set XJ. To derive the time, based on the state-space expansion conditions, the probability exponential form of the CME Eq. (5) is evaluated for approximation up to the desired final time tf in steps. To focus on the probable states that contribute most to the probability mass in the domain, we first define the set of non-probable states (those which have the least probability mass) as \( {\mathbf{X}}_K^{\prime } \), which are to be bunked. The number of states will usually be infinite, without selecting probable states for the domain. By doing this we can avoid recalculating the probabilities and decrease the computational efforts by keeping the domain small. This bunking can also be applied to the initial distribution of the system at t0. If submatrix \( {A}_j^{\prime } \) contains the non-probable set \( {\mathbf{X}}_K^{\prime } \) of states, then the probability of set will be,
The criterion for defining the non-probable states is determined by the τm tolerance value. \( {A}_j^{\prime } \) will only be considered to have non-probable states if,
Similarly, submatrix Aj has a probable set XK of states if P(t)(XK) ≥ τm otherwise, the states from XK are bunked to \( {\mathbf{X}}_K^{\prime } \) if P(t)(XK) < τm. For any iteration, if \( {P}^{(t)}\left({\mathbf{X}}_K^{\prime}\right)\ge {\tau}_m \) then (from Eq. (11)) some states from \( {\mathbf{X}}_K^{\prime } \) return to XK in the next iteration to increase the accuracy of the approximate solution (Ӕ). The column sum of the approximate solution (Ӕ) of these states is defined as:
where, I = (1, …1)T is of an appropriate length. Declaring some states as non-probable and removing them before calculating the probabilities as seen in [28] will decrease the accuracy of Ӕ with the cumulative step errors. This can be validated from the state probabilities that have been ignored in the domain:
We define the step error in terms of the probabilities bunked. If \( {e}_{rror}\propto {P}^{(t)}\left({\mathbf{X}}_K^{\prime}\right) \) then,
Every expansion step explores at least one new state and change {XK} but not necessarily \( \left\{{\mathbf{X}}_K^{\prime}\right\} \) if:
is satisfied. For ideal systems with a given initial probability of \( {P}^{\left({t}_0\right)}\left({X}_0\right) \), the \( \left\{{\mathbf{X}}_K^{\prime}\right\} \) should be null and so \( {P}^{\left({t}_f\right)}\left({\mathbf{X}}_K^{\prime}\right)=0 \). For such systems \( \left\{{\mathbf{X}}_K\right\},\left\{{\mathbf{X}}_K^{\prime}\right\}\ \epsilon\ \left\{{\mathbf{X}}_J\right\} \) for final projection and,
\( {P}^{\left({t}_f\right)}\left({\mathbf{X}}_J\right) \) in Eq. (18) is the solution of Eq. (3) after the state-space is expanded to XK. However, for large biochemical systems, Eq. (18) may not hold completely true, due to the nature ((fast (RM(fs)) and slow (RM(sr))) of some reactions present in the system; therefore, the condition in Eq. (11) will pass the states from \( {\mathbf{X}}_K^{\prime } \) to XK. The states with the lowest probabilities will be bunked when:
This improves the solution. Removing without calculating the probabilities of some states is one of the lags of the current methods [18, 20, 21, 24, 26,27,28]; it is a result of achieving the truncated domain and saving computation time. To address this, we set a \( {P}^{(t)}\left({\mathbf{X}}_K^{\prime}\right) \) leakage point based on:
where, τm(leak) for systems will reform Eq. (16) as:
which would then zip the \( {\mathbf{X}}_K^{\prime } \) further by leaking the highest probabilities to XK so that the probability sum is no longer conserved. The motivation of setting this ration is to reconsider (up to 40% of \( {\mathbf{X}}_K^{\prime } \)) the bunked states to improve the Ӕ solution and decrease the expansion step error. While modeling the biochemical system, if the slow and fast reaction [12] criterion is considered during expansion, then τm(leak) will be defined as,
We consider Eq. (21) criterion for all the computational experiments in this study. The conditions in Eqs. (21) and (22) will lead to an optimal set of states as,
at td in the domain. When XK is updated at every tstep before reaching tf, this creates several intermediate domains which we define as Bound. At t0, the domain only has the initial state of the system; therefore, we define the Bound as:

After a single tstep of expansion, if XK is updated with a new state or set of states, it creates:

at td. Here, ƌl denotes the depth level of the latest state or set of states that has been added in the domain to form Boundupper. This Boundupper is re-labeled and considered as Boundlower for the next tstep of the expansion. If the expansion is to be limited in the number of Bounds, then every count(ƃlimit) leads to:

where, ƃlimit is the bound limit. For example, if ƃlimit = 2, then the count(ƃlimit) will be from \( 0\overset{\mathrm{to}}{\to }1\overset{\mathrm{to}}{\to }2 \). If the count(ƃlimit) is increased to ƃlimit for Itrth iterations, then Boundupper in the current iteration will be Boundlower for the next iteration. Every Boundlower state will be the strict subset of every consecutive Boundupper given as:
and the upper bound as:
where Z is the number of Bounds (or intermediate domains). The 2D pyramid domain in Fig. 3 graphically illustrates the increase in the population of states in the domain with the increase in iterations (Itr). The apex of the pyramid represents the initial state X0 of the system at Boundlower(1) at t0, whereas the base represents the deepest level where the system ends with the final domain carrying set XK with the maximum probability mass.
For large biochemical systems, the number of created Bounds are based on Itr. They have million/billions of states. Expansion can be terminated by defining time tf at which the solution is required. To have an auto break-off point in the expansion, it is first necessary to define the criteria that limits Itr or when no more new states can be searched. Therefore, we define this criterion in the following section. This criterion also applies to biochemical systems which have fast and slow reactions [12].
Cease of criterion after updating
In every expansion step, the domain is validated by Eq. (21) and new states are added in XK as long as:
is satisfied for probable states and stops if Eq. (29) is not satisfied. This leads to a point at tf where error < τm, but the expansion can be extended to meet accuracy requirements by re-considering the criteria as:
before steps to tf. However, the size of XK obtained through Eqs. (30), (31) and (32) at tf will be greater compared to the size of XK obtained by Eq. (29) at tf, as the latter will have fewer states. In Eqs. (30), (31) and (32), with the increase in the size of Aj, the value of the left-hand side will also increase, resulting in an improvement in Ӕ. When considering any Markov process of a biochemical system of any size in which the probability density expands according to Eq. (3) then Eqs. (30), (31) and (32) will approximate the solution within \( {\tau}_m\ast \frac{\left(\mathrm{no}.\mathrm{of}\ {R}_{M(sr)}\right)}{\left(\mathrm{no}.\mathrm{of}\ {R}_{M(fs)}\right)} \), \( {\tau}_m\ast \frac{\left(\mathrm{no}.\mathrm{of}\ {R}_{M(fs)}\right)}{\left(\mathrm{no}.\mathrm{of}\ {R}_{M(sr)}\right)} \) and τm(leak), respectively, of the true solution of the CME, which is Eq. (3).
Computational experimental results
The ISP method is initialized and parameterized using the initial conditions of the models. Due to a large number of mathematical operations and equations, simultaneous parameter predictions with a limited number of experimental values is often complicated for dynamic systems. Therefore, the consistency with the available experimental data was ensured at each step of the ISP. This method has led to the successful development of several functions that integrate large number of processes supporting extensive expansion of the state-space.
To demonstrate the ISP LAS algorithm, we first consider the catalytic reaction system [37] defined by the reactions
depicted as a network in Fig. 4 as:
Catalytic reaction network with five \( \widetilde{\mathrm{N}}=5 \) species S, B, C, P, and E in a network defining reaction, as given in Eq. (33)
In this biochemical system (dimension = 5), reactant P will transform into product E via complex B when reactant S acts as a catalyst for the reaction and produces C. We rewrite this catalytic reaction system as a network of three reactions:
with the initial copy counts S0= 50, P0= 80, B0 = C0 = E0 The reaction rate parameters are k1= 1, k2= 1000, k3= 100. These species counts are used as a state-space to define the model and these copy counts are tracked as \( \left(\left[S\right],\left[B\right],\left[C\right],\left[P\right],\left[E\right]\right)\in \widetilde{N}:= \left({x}_0,{x}_1,{x}_2,{x}_3,{x}_4\right) \).
In reaction R1, the copy count of S is reduced by 1, which increases the copy count of B by 1. In reaction R2 the copy count of B is reduced by 1, which increases the copy count of C by 1. In contrast, reaction R3 decreases the B and P counts by 1 and increases the B and E counts by 1. As in R3, B acts as a catalyst to convert P to E and B is retained in the same reaction. We can now define the transitions associated with R1, R2, R3 in the stoichiometric vector VM matrix as:
For LAS method compatibility, the associated Markov chain of this model is converted into a Markov chain tree with the states in terms of the nodes with additional information such as the number of RM reactions required to reach the state. In the growing Markov chain tree, the transition between the nodes:
is defined in the typical form of the dictionary Dict. We express the propensity functions of the three reactions in terms of the states \( \left(\left[S\right],\left[B\right],\left[C\right],\left[P\right],\left[E\right]\right)\in \widetilde{\mathrm{N}} \). Node N1 = (X0, ƌ1) carries the initial state X0 of the system at an initial depth of level 1. Further, nJ = (XK, ƌ1, 2, …) is expanded and the states updated by following the LAS order. The corresponding propensities ∆ai,j are updated in the Ai,j matrix in every iteration, based on the LAS updating trend (for example, see SI 2). The system began with S0= 50, P0= 80. Gradually all the reactants are transformed to products, E and B. The system ends in nJ = (X1, 2, ……14666, ƌl).
Figure 5 shows the LAS method’s response when solved with τm = 1e − 6 for tf = 0.5 sec. Due to the nature of the model reaction rates, small steps tstep = 0.01 sec are taken to capture the moments based on non-negative, non-zero states for the domain. LAS successfully creates the domain of an optimum order, with 14666 states at tf, by introducing the new states to the domain with time, as shown in Fig (a) in Fig. 5. This pattern demonstrates that the frequency (the number of states at any time t) of expansion increases in depth when the number of active reactions increase in the system. With the addition of probable states, the domain contains enough probability mass to approximate the solution up to tf. The states are updated in sets as seen in Fig (b) of Fig. 5, for the catalytic system after every iteration.
Expansion and updation of the states and set of states explored for the catalytic reaction system using the LAS method. (a) demonstrates that state-space expansion increases the number of new states in the domain. The size and colour of  shows the increase in the size of the domain with the states’ population. In (b), LAS unfolds the state-space pattern to update the states in the domain and expands 14666 probable states in 0.5 secs
shows the increase in the size of the domain with the states’ population. In (b), LAS unfolds the state-space pattern to update the states in the domain and expands 14666 probable states in 0.5 secs
The state-space pattern in Fig (b) of Fig. 5 can be used as a blueprint of the catalytic systems’ state-space to compare with other model’s blueprints for their characteristics and occurrence of reactions. Such a pattern can be used to predict the behavior of large network state-space expansions when the set of occurrences of the initial reactions are similar in different systems. The solution of Eq. (5), up to tf, for the domain created by LAS, is shown in Table 1. The system’s conditional probabilities based on its species are shown in Fig. 6.
In three test runs, the ISP LAS run time for the catalytic system was 4677 secs when solving Eq. (5) with 14666 states. The probability of the species in Figure SI 17 (see SI 9) shows the nature of the reactions affecting each species’ count in the system. The involvement of species B in all the reactions results in its highest probability at tf. Species B also acts as a catalyst for R3, converting species P to E; therefore, both have equal probabilities at the time of solution.
Figure 6 shows the total probability bunked at t′ while progressing with the expansion. Bunking produces an error (w.r.t approximation), with time when the number of states increases with the expansion. LAS produces minimal error of order 10−5, as given in Table 1.
To demonstrate the ISP LOLAS algorithm, we consider the coupled enzymatic reactions defined by the reactions
depicted as a network in Fig. 7 as:
This biochemical system (dimension = 6) describes two sets of enzymatic reactions transforming species S into species P and transforming species P back into S. We rewrite C reactions system as a network of six reactions:
with initial copy counts S= 50, E1= 20, E2= 10, C1 = C2 = P= 0 and reaction rate parameters of k1 = k4= 4, k2 = k5= 5, k3 = k6= 1. These species counts are used as a state-space to define the model. These copy counts are tracked as:
As in the previous example, we can now define the transitions associated with R1, R2, R3, R4, R5, R6 in the stoichiometric vector VM matrix as:
For the LOLAS method, the associated Markov chain of this model is converted to a Markov chain tree with the states in terms of nodes with additional information, such as the number of RM reactions required to reach the state. In growing Markov chain tree, the transition between the nodes:
is defined in the typical form of the dictionary Dict. We express the propensity functions of the six reactions in terms of the states \( \left(\left[S\right],\left[{E}_1\right],\left[{C}_1\right],\left[P\right],\left[{E}_2\right],\left[{C}_2\right]\right)\in \widetilde{\mathrm{N}} \).
Node N1 = (X0, ƌ1) carries the initial state X0 of the system at the initial depth (level 1). Then nJ = (XK, ƌ1, 2, ……) is further expanded and the states updated by following the LOLAS order. The corresponding propensities ∆ai,j are updated in the Ai,j matrix in every iteration, based on the given LOLAS updation trend (for example, see SI 2). Initially, the system started with S= 50, E1= 20, E2= 10. Gradually all reactant species were transformed into products resulting in the system ending in nJ = (X1, 2, ……8296, ƌl).
Figure 8 shows the LOLAS method response when solved with τm = 1e − 6 for tf = 2.0 sec. Due to the nature of the model reaction rates, small steps tstep = 0.01 sec are taken to capture the moments. These are based on non-negative, non-zero states for the domain. LOLAS successfully creates the domain of an optimum order with 8296 states at tf by introducing the new states to the domain with time, as shown in Fig (a) of Fig. 8. In Fig (b) of Fig. 8, demonstrates that the frequency (the number of states at any time t) of expansion increases in depth when the number of active reactions increases in the system. With the addition of probable states, the domain contains enough probability mass to approximate the solution up to tf.
Fig (a) of Fig. 8 depicts state-space expansion which increases the number of additions of new states in the domain. In Fig (b) of Fig. 8, ISP LOLAS unfolds the state-space pattern to update states in the domain and expands 8296 probable states in 2.0 sec. As a blueprint of the dual enzymatic reaction network, the state-space pattern in Fig (b) of Fig. 8 can be compared with other model blueprints in terms of its characteristics and reactions. Such a pattern is considered to predict the behavior of a large network state-space expansion when the set of occurrences of the initial reactions are similar in different systems. The solution of Eq. (5), up to tf, for the LOLAS-created domain is shown in Table 2. The system’s conditional probabilities based on species are shown in Figure SI 18 (see SI 10)
In three test runs, ISP LOLAS′ run time for the dual enzymatic reaction network was ≈1614 secs when solving Eq. (5) with 14666 states. The probability of the species in Figure SI 18 (see SI 10) shows the nature of the reactions which affect each species’ count in the system. At tf, the probabilities of E2 and C2 remain high compared to E1 and C1 at different molecular counts. This results in a low probability of P compared to S. We know that this network transforms species S into species P and then transforms species P back into S. Based on the current probabilities of the species at tf, the future probability of P will increase. S will remain the same or decrease. With this change, the probabilities of E2 and C2 decrease in comparison to E1 and C1.
Figure 9 shows the total probability bunked at t′ while progressing with the expansion. The bunking produces an error (w.r.t approximation) with time when the number of states increases with the expansion and provided that, LOLAS produces a minimal error of order, 10−5, as given in Table 2.
We extend the application of our ISP method to simulate a large model of the G1/S network [38] under the condition of DNA-damage. We want to determine the number of states at different points in time and predict the conditional probabilities of the protein species based on events leading to the formation of different complexes in the system.
The G1/S model (dimension = 28) with a DNA-damage signal transduction pathway is considered to be very stiff in nature, so while some molecular counts of certain proteins increase very rapidly others do so slowly. This makes it tough to solve, even for a short time period. The model is solved for tf = 1.5 sec with ƃlimit = 1, τm = 1e − 6, tstep = 0.1. The systematic exploration of nodes carrying probable states are undertaken in a similar way as discussed in Table SI 4 of SI 3 and depicted (see Figure SI 7 of SI 3) in six stages (denoted as \( \hat{\mathrm{S}} \)), representing RM reactions with propensity, aμ, with the arcs as transitions.
The nodes are expanded up to tf to enable identification of the reaction channels responsible for variations in the proteins. From the transitioning factor of the 2nd-tier, we can see that every node has an average of at least ≈97 possible child nodes carrying states. Further, Dict is expanded for n-tiers of the child nodes to add more states to the domain. Additionally, nJ = (XK, ƌl = 1,2,……) is expanded and updated, as per the ISP LOLAS trend (see Table SI 5 of SI 3).
The ISP LOLAS method response for the number of states in the domain and time, t, is shown in Fig. 10. The initial response suggests that only a few reactions were active until t= 0.4 sec. After that time, more reactions triggered that explosively take the exploration above 0.5 million states in 0.5 sec. For such a large model, this combination of explosion states was expected as proteins undergo several excursions due to the number of reactions in fractions of time, t. The second explosion of states occurs after 1.0 secs when almost all the reactions (involving the species, given in SI 4.1) become active in the network. The size and colour of the 2D pyramid in Fig (a) of Fig. 10 shows the increase in the size of the domain with the state explosions. The number of sets of states that create the bounds at t are shown in Fig (b) of Fig. 10. With the exploration of the set of 517584 states, the Bound(3)upper = {X0, 1, 2…..604677} is formed at 0.5 sec carrying 604677 states. Some states were bunked at 0.5 secs resulting in approximation errors that reach 2.42e − 06 at 0.6 sec. At tf, the LOLAS ends up with a domain defined by Bound(4)upper = {X0, 1, 2…..3409899} carrying 3409899 states with 3.52e − 06 approximation errors.
Fig (a) of Fig. 10 demonstrates that the state-space expansion increases the number of additions of new states in the domain. ISP LOLAS quickly expands the state-space up to ≈3.5 million states in 1.5 secs. In Fig (b) of Fig. 10, ISP LOLAS unfolds the state-space pattern to update states in the domain and expands 3409899 states up to tf.
The corresponding propensities, ∆ai, j, are updated in the Ai, j matrix in every iteration, based on the ISP LOLAS update trend. The system started with the initial state of the protein species and gradually, as protein levels change in the system, it exploits the copy counts that shift the system to a new state. The change in protein levels causes the system to transform into new states: here we see the manifestation of the Markov process of the system. The ISP LOLAS captures this process and defines several bounds of the domain at different time intervals, as indicated by the pyramid in Fig. 3. To investigate the expansion of states more closely, the order of bounds at different time intervals, and the number of states present in the bounds, are provided in Table 3. The size of bound created in each duration reveals that for every step, the growth of the domain is eight-to-ten times the previous size of the domain.
The set of nodes N1, N2, . . …N3409900 carries unique states representing the set of state(n3409900) = (X0, 1, 2, …3409899) that forms the state-space of the model. It is important to note that some proteins are synthesized and promoted by the network itself, as evidenced by some reactions of the pathway, which increase the frequency of the repeated states. However, ISP LOLAS validation does not consider them for the domain. Equation (5)’s solution, up to tf for the domain, created by ISP LOLAS, is shown in Table 4.
Over three test runs, the ISP LOLAS′ run time for the G1/S model was 1372 secs for solving Eq. (5), with the optimal domain having 3409899 states. The ISP LOLAS response given in Fig. 11, shows the system’s probabilities bunked at t′ during the expansion (w.r.t approximation), when the number of states increases with the expansion, and provided that ISP LOLAS produces minimal errors of the order of 10−6, as given in Table 4 and Fig (a) of Fig. 11. We set the checkpoint to examine the initial state’s probability over time. The response in Fig (a) of Fig. 11 indicates that the probability of the system remaining in the initial (normal) state decreases with time in the presence of DNA damage, which triggers the change in protein levels.
The ISP LOLAS′ response for total probability bunked at t′ from the domain and checkpoint for examining the initial state probability over time. (a) shows how ISP maintains accuracy by keeping low errors. (b) shows the decline in the probability of the system remaining in the initial state in the presence of DNA damage
The conditional probabilities of the species’ systems are given in Fig. 14 and SI 8. In the case of DNA-damage, large numbers of the most notable parameters increase, compared to normal conditions (in cell cycle progression). The increase is predominantly related to x14 (p21) having a high initial probability, see Fig(14) of Figure SI 19 (see SI 11). The feedback (negative) of x24 (p53) increases its probability, see Fig(24) in Figure SI 19 (see SI 11), such as the association rate of x16 (p21/CycE/CDK2 − P), the rate of synthesis of x14 (p21) by x24 (p53), the rate of degradation of x14 (p21), and the rate of synthesis of x24 (p53) by DNA-damage signal. The conditional probabilities of the two key proteins, x10 (p27) and x1 (CycE), are affected by the change in the cell’s response to the level of the DNA-damage signal, see Fig (10) and Fig (3) in Figure SI 19 (see SI 11). The parameters related to x10 (p27), as well as x1 (CycE), greatly affect the probability of x21 (E2f) with time, see Fig (21) in Figure SI 19 (see SI 11). The impact of x1 (CycE) involves additional parameters related to CycA, because the release of supplementary x21 (E2f) depends on x20 (Rb − PP/E2f) hyperphosphorylation by the activation x7 (CycE/CDK2 − P), which affects the probability of x21 (E2f).
When the release of x21 (E2f) is affected, the probability of x1 (CycE) increases, see Fig (3) in Figure SI 19 (see SI 11). This leads to the progression to the S-phase, followed by the temporary suspension of cell cycle progression. The increase in probability of x24 (p53) shows cell support to repair the DNA damage. The parameters and the probabilities relating to x14 (p21) and x24 (p53) become important in the case of DNA damage. When combined, the conditional probability of these parameters indicates the involvement of the DNA-damage signal in the transition of G1/S.
Discussion
In this section, we discuss ISP performance, focusing specifically on the speed and accuracy of the expansion, domain size and accuracy of the solution in comparison with other methods.
Comparison with other methods
An approximation of 10−5 is used to find the approximate number of realizations required by the SSA for the 10−4 global error. Realizations were computed until the difference was less than 10−4 between the known distribution and the empirical distribution.
Approximately 106 and 105 runs were required to obtain the right distribution for the catalytic and dual enzymatic reaction networks, respectively. In the catalytic system, we observe (see Table 5) that both versions of ISP are faster than the OFSP of r-step reachability and the SSA of sliding windows. We attribute this greater efficiency to LOLAS having fewer states and less computational time than the OFSP method. LOLAS has better accuracy at tf. Similary, the ISP was much faster than the SSA, and the total number of realizations required from the SSA to have an error at tf still large than that of LOLAS is 106. In the dual enzymatic network, we observe (see Table 5) that both versions of ISP are faster than the OFSP of r-step reachability and the SSA of sliding windows; we attribute the improvement to both ISP variants having an efficient domain with a small approximation error and less computational time than that of the OFSP method and better accuracy at tf. Similarly, both ISP variants were much faster than SSA, as the total number of realizations required to have an empirical distribution with the error at tf is ≈12 times more than the domain produced by ISP.
We also compared the error at tf to determine the solution’s efficiency. As seen in the results, the increase in the step error in OFSP affected the solution at tf. Figure 12 (see Fig (a) and (b)), compares the ISP (LAS and LOLAS) with OFSP on the basis of the approximation error at t during the expansion of the catalytic and dual enzymatic reaction networks, respectively. Addressing the step error in ISP and the selection of the probable states results in a more efficient solution at tf compared to OFSP.
The typical firing nature of reactions in the catalytic system makes them stiff. Therefore, the selection of states becomes difficult to approximate. While some species in the system increase abruptly, others do so very slowly because the kinetic parameters (k1= 1, k2= 1000, k3= 100) have large differences: this triggers reactions at different rates. Reaction R1, is categorized as a slow reaction in the network: it affects the fast reaction, R2. As the computation results of Table 5 show, the ISP found that only 13089 probable states were required to solve the system up to tf. This not only saves computational time (see Fig. 13) compared to OFSP and SSA, and improves the solution’s accuracy. In OFSP, applying the compression at every step or after a few steps is still computationally expensive for a model like the catalytic reaction system, as seen in Table 5 and Fig (a) of Fig. 13.
The network shown in Fig. 7 consists of two interlinked enzymatic reaction systems. These systems transform species S and P into each other via the other species, making the system stiff in nature. The selection of states thus becomes difficult for approximation. This is due to some species (S and E1) in the system increasing abruptly, while others take longer to increase. Some of the kinetic parameters (k1 = k4= 4, k2 = k5= 5) have large differences from other kinetic parameters (k3 = k6= 1): this triggers reactions at different rates. Categorized as the fastest reaction in the network, R affects species S, C, E. It is followed by other reactions involving other species. As the computation results in Table 5 show, the ISP LAS indicated that only 8282 probable states are required to solve the system up to tf. Likewise, ISP LOLAS identified that only 8296 probable states are required to solve the system up to tf This saves computational time (see Fig. 13), compared to OFSP and SSA, and improves the solution’s accuracy. In OFSP, applying the compression at a defined step or after a few steps is still computationally expensive for models like the dual enzymatic reaction system, as seen in Table 5 and Fig (b) of Fig. 13.
The total computation effort required at every step, when compressing the number of states up to tf, is approximately equal to the total computation effort required when the compression is applied in the gaps in some steps on a set of states up to tf. Moreover, the state-space will remain the same at tf , regardless of when the compression is applied.
A comparison of the computational times in Table 5 shows that both versions of ISP are significantly faster than other methods. Figure 14 shows the CPU utilization (%) of LOLAS and OFSP with respect to run-time (minutes). The dedicated throughput (see SI 1.1) between EC2 and EBS was not used to solve the model. The average CPU exertion is about 60%, which is a considerable workload for a given model. The expansion and approximation began when CPU use was at ≈1.6422% in the catalytic reaction system and ≈1.23% in the dual enzymatic reaction system, at t= 0 sec. It increases up to 60.0% and then drops down to zero at tf.
AWS® CPU utilization percentage, when the catalytic reaction system is solved up to tf= 0.5 sec, and the dual enzymatic reaction system solved up to tf= 2.0 sec, using OFSP and LOLAS. The performance analysis was carried out using CloudWatch® (Statistic: Average, Time Range: Hour, Period: 5 Minutes)
Theoretical interpretation of methods
Although, SSA recognizes the support and wastes no time in searching for the right domain and creating independent realizations which can be run parallel on multi-core environment, solving the system via Eq. (5) is quicker than creating realizations via stochastic simulation [39,40,41]. This is because the N-term approximation [42, 43] of the probability distribution to create the required number of realizations is always less than, or equal to, the minimal support approximation up to same error. These realizations were computed until the difference was less than the prescribed approximation between the known distribution and the empirical distribution. In terms of the system dimension, which is usually defined by the number of species in the system, the approximation of Eq. (5) in ISP becomes smaller problem to solve compared to approximation through SSA. This enables ISP to perform better.
In contrast, OFSP creates a hyper-rectangle and applies truncation to guarantee the minimal order domain for the approximation. OFSP truncates the state space after every few steps to ensure the minimum size of the domain and enable greater computational speed. However, differences in reaction firing changes the probability of some states at a later stage; therefore, truncating the state space in OFSP after every few steps or at every step would remove probable states from the domain, which in turn would affect the accuracy of the solution. As a result of this, OFSP′s overall performance is compromised. In contrast, ISP first explores the states based on guided exploration through the BLNP function (see method section (a)) and then leaks the set of states \( {\mathbf{X}}_K^{\prime } \) which have the lowest probabilities in the bunker at t′ without removing them (see Eq. (20)). It recalls these sets of states when the probabilities of these states increase at later time.
In ISP, the time and space complexity (refer to SI 7) of removing and accessing the states in the bunking and recalling process is optimum, compared to the overall time and space complexity of the truncation step in OFSP [20]. As seen in Table 5, the number of states present in the domain for the catalytic reaction network in ISP LAS is approximately equal to number of states present in the domain produced by OFSP. Additionally, the number of probable states in the domain for the dual enzymatic reaction system in ISP LAS is quite more as compared to the domain produced by OFSP. However, better complexity and the guided selection of probable states for the domain produces low approximation errors and means that ISP LAS performs better overall than OFS. Similarly, ISP LOLAS outperforms OFSP in finding the optimum domain due to its bi-directional exploratory nature (see methods section (c)). This feature helps ISP LOLAS to achieve a more accurate solution (see Table 5 and Fig. 12) as well as a quicker computational time (see Fig. 13). These benefits are also due to fact that ISP visualizes the state-space as a Markov chain graph or a tree (see Markov chain as a Markov chain tree section) which ultimately decreases the complexity in the expansion phase.
Conclusions
This paper has introduced a novel approach, ISP,to model biochemical systems. This new approach addresses both performance and accuracy problems in CME solutions. Provided all probable states are not added into the domain, up to the desired tf, variants of ISP (LAS and LOLAS) provide systematic ways of expanding the state-space. We have demonstrated the effectiveness of our methods with several experiments using real biological models: the catalytic reaction system, the dual enzymatic reaction system, and the G1/S model (large model). The results and the algorithm’s responses reveal improvements in how different sized biological networks can be modeled: even state-spaces with 3409900 nodes (see Table 3) carrying states up to ≈3.5 million can be explored within a reasonable time. The results also show that the domain laid out by ISP had an optimal order and was successful in finding probable system states, all the while maintaining high levels of accuracy and efficient computational timing.
We have compared the ISP results against two popular methods: OFSP (r-step reachability) and SSA (τ leaps adaptive). ISP outperformed the other methods, in computational expense, accuracy and projection size. The ISP was more effective in terms of predicting the behavior of the state-space of the system and in performance management, which is a vital step in modeling large biochemical systems. Unlike other methods, the ISP keeps the lowest states probabilities in the bunker without removing (as removed in OFSP) them, before calculation (as removed without calculation in FSP GORDE). It computes the probabilities at t without computing large numbers of realizations (as done in SSA).
The diverging nature of the ISP response, with respect to OFSP in Fig. 19, also shows that the solution improved with t and at a higher tf. For example, in the large model (case study 2), the computation time was 1372 sec and the solution was 3.52e − 06 at tf, which was lower than the small model results (the catalytic reaction system). These results show ISP’s compatibility with the distinct size of biochemical models.
These examples have demonstrated that ISP is a very promising technique for system’s biology. For stiff models, such as the G1/S and Candida albicans models, the ISP yielded plenty of information. Likewise, it provided opportunities for stochastic analysis of large models. ISP can be used to compute the probabilities of the species up to the required time. One could also use ISP to conduct robustness and sensitivity analysis on the dynamics of biochemical systems and to keep track of what reactions are more active in the system at a particular time. ISP is also able to determine the complexity of the system by defining the bounds with number states and keep track of the nested state-space patterns (called the ISP model blueprint) that were updated at the end of each step. Outlining the patterns of expansion of states to predict the projection folds can be used for updating the new states.
We anticipate that the current structure of the ISP variants can be employed for different classes and varieties of biological systems. Additionally, they can be used to compute the configurations with many reactions, as long as the notable part of the state-space density is present between Bound(Z)lower and Bound(Z)upper. When there was a high probability of the molecular population of the species undergoing several excursions in a fraction of time, then the ISP uses a small tstep to capture these moments. While such computations were still challenging in the expansion phase for typical models they can be addressed more closely in combination with the second part of the CME solution: that is, the approximation phase. There are several methods which can be used to address these challenges.
Approximation methods, such as the Krylov sub-space, can be used to effectively compute the matrix exponential times of a vector. While it was mathematically attractive to aggregate the states or decompose the large sparse matrix into a small dense matrix using the Krylov sub-space, this method may not be computationally efficient in the absence of an efficient domain. Performance can also be enhanced by employing the fast math functions, compatible with the multicore environment. We have clearly outlined the core ideas behind the ISP variants. We have highlighted the differences and similarities between them and other methods that cover the computational and theoretical considerations that are essential before any of the approximation methods becomes feasible for an efficient CME solution.
Methods
To understand and predict the dynamics of the state-space response in biochemical systems, we have developed an analytical numerical method called ISP. This method integrates the reactions’ propensities describing the Markovian processes through set of nodes governing set of states of the system. The two variants of ISP, named LAS and LOLAS, consist of several modules that incorporate sets of inputs and functions within several compartments. Figure 15 depicts all the ISP modules. The integrated form is discussed later in Tables 7 and 8.
Comprehensive ISP method flow chart. A description of the modules (steps), sub-modules and the list of components are discussed in SI 5
These modules and sub-modules constitute the ISP method. They track key changes in the components that follow changes in the reaction propensities by population and activation of the species. The modules also describe the dynamics of the biochemical system. The method also permits the time form quantification of state-space based on the size and model dimension.
The ISP states expansion strategy is based on the Artificial Intelligence (AI) standards [44,45,46,47], state-space search and relative successor (Suc) operator or function which perform operations on inputs. AI refers to the study of intelligent agents [48] of a system that perceives and takes action to successfully achieve goals. Most of the problems can be formulated as searches. They can be solved by reducing to one of searching a graph or a tree. To use this approach, we must specify the successor operator which defines the sequence of actions leading from initial to goal state at different time intervals, that lead to the solution.
In terms of AI, we define the state-space as a set of states in the system we can get to by applying Suc to explore new states of a biochemical network. Suc can be applied explicitly, which maps the current state to the output states, or defined implicitly, in that it acts on the current state and transforms it into a new state. In the state-space graph for biochemical networks, we do not define the goal state (or end state) explicitly. Instead, it is defined by Suc implicitly in intervals based on the nature (fast, slow, reversible and irreversible) of the reactions in the system, the duration of expansion and the introduction of stochasticity into the system. This should systematically expand the state-space from XK at t to XK + 1 at t + 1 by going through each node nJ at depth ƌl of the Markov chain graph to evaluate the Markov processes; the expansion aims to occupy most of the probability mass during [XK + XK + 1], and the Markov processes can be solved for probability distribution at t + 1.
Where XJ is the finite set of states and Gmc = (XJ, Vμ) is the Markov chain graph on XJ associated with A = [ai,j], given X0 as the initial state and XK as the set of the explored state, where X0 ∈ XK then the implicit successor is defined as,
Equation (44) gives the new states of the system, where, Vμ is the set of stoichiometric vectors vμ function defining the state transitions from any present state Xi ∈ XK to new state \( {X}_{i^{\prime }}\notin {\mathbf{X}}_K \). The sample space in the graph contains the unique state of the system stored in a transition matrix, which satisfies Eq. (7) conditions. This transition matrix is a compressed row format (CSR) [49, 50] based on an index of rows ⟶ columns delimited by commas generating the dictionary Dict of the model which defines the transitions between nodes in the state-space and the mapping of states. Through Suc, we can know nothing more than the neighbors (child nodes) of the current node (states reachable through a single reaction). We then consider these neighbors (child nodes) as our only goal states; there can be many in numbers. In a situation such as this, search trails are referred to as blind or uninformed searches. In the following section, we discuss the infrastructure of an uninformed search, the type of data structure we will be dealing with.
Infrastructure for searching
A data structure is required to retain the search track in the graph for problem state-space expansion. For each node, Ni, of the tree, we create a structure consisting of five elements:
-
(1)
Ni.State: represents state Xi in the state-space corresponding to Ni;
-
(2)
Ni.Parent: represents the parent node of the child node Ni;
-
(3)
Ni.Depth: represents the depth of state state Xi;
-
(4)
Ni.Cost: represents the cost \( {C}_{N_i,{N}_i^{\hbox{'}}} \) of the transition from Ni to \( {N}_i^{\prime } \) in the state-space;
-
(5)
Ni.Action: represents the action applied via Suc on the parent node to reach Ni.
To explore new states in the system, we consider the initial state state(N1) = (X0, ƌl) as input to the successor, Suc. Once the expansion is initiated, the Dict will temporarily (in run-time) store the information for the transition from one node to another in the state-space that binds to the reaction propensities aμ. This shift is denoted by an arrow →, which shows multiple transitions from the parent nodes to the child nodes containing the end state. The set of nodes \( {\mathbf{n}}_J=\left\{{N}_1,{N}_2,\dots ..{N}_{S^{\widetilde{\mathrm{N}}}}\right\} \) is a data structure that incorporates the Markov chain graph Gmc. We explore all the nodes that store the set of states XK as well as some additional information about the state, such as the depth and transition cost, from one state to another in the system. If a set of states(nJ) = XJ, then \( {C}_{N_i,{N}_i^{\hbox{'}}} \) is the transition cost to reach \( state\left({N}_i^{\prime}\right)={X}_{i^{\prime }} \) from state(N1) = X1 and depth(nJ) = ƌl defines the depth of the set of nodes in Gmc, then the standard relation between a set of nodes and a set of states is given by nJ = (XJ, ƌl) or  and the standard relation between a single node and a single state is given by Ni = (Xi, ƌl) or
and the standard relation between a single node and a single state is given by Ni = (Xi, ƌl) or  if the transition cost is considered.
if the transition cost is considered.
For example, Fig (a) of Fig. 16 shows the Markov chain graph, Gmc, with nJ = 10, ƌl = 4. Its equivalent tree Ѭ is shown in Fig (b) of Fig. 16 with nJ = 15, ƌl = 5. In the tree nodes N1 = N11 = N12 carries the same state, X1 at ƌl = 1, 2 and 3, respectively, where walk N2 → N11 and N7 → N12 represent the backward reaction of the forward reaction represented by walk N1 → N2 and N1 → N7, respectively.
The set of nodes with states are represented as


In general, the transition cost,  , is defined as:
, is defined as:

 is the summation of all the propensities aμ of the RM reactions that take the system to its final state. For example,
is the summation of all the propensities aμ of the RM reactions that take the system to its final state. For example,  to expand to state(N10) = X10 of Fig (a) of Fig. 16 is given by
to expand to state(N10) = X10 of Fig (a) of Fig. 16 is given by

If these are the possible paths for the expansion that expands XK at every iteration then  will be defined by the only path that has the lowest \( {P}^{(t)}\left({\mathbf{X}}_K^{\prime}\right) \). This can be generalized as follows:
will be defined by the only path that has the lowest \( {P}^{(t)}\left({\mathbf{X}}_K^{\prime}\right) \). This can be generalized as follows:

which means that in order to minimize the expansion cost for the optimal domain XK at least one path should have states with high probabilities for XK. It is best to follow the path with  , which leaks the minimum probabilities of the system.
, which leaks the minimum probabilities of the system.
For large biochemical models, there exist infinite cases when the node is unreachable from the initial or another node; such cases are ignored when  because some probabilities are always dropped in the approximation. Therefore,
because some probabilities are always dropped in the approximation. Therefore,  as defined by the lowest \( {P}^{(t)}\left({\mathbf{X}}_K^{\prime}\right) \) is strictly limited to,
as defined by the lowest \( {P}^{(t)}\left({\mathbf{X}}_K^{\prime}\right) \) is strictly limited to,

Upon expanding the root node N1, we expand the child nodes carrying new states, and then the child-child nodes are explored. The walk between nodes Ni \( \overset{V_{\mu}\left({\mathbf{X}}_K(t)\right)}{\to } \) Ni + 1 is defined by dictionary Dict. This represents the occurrence of RM reactions through M elementary channels. For Fig (a) of Fig. 16, the typical form of dictionary is given below:
and is indexed with the propensities, [ai,j], for all the RM reactions. As the propensities are changing by ∆ai,j, we consider the recent values of ai,j in every iteration of ISP that corresponds to the reactions involved. To make the  feasible for any type of biochemical system (stiff, non-stiff) to capture probable states, it is important to consider the expansion cost for small tstep (time step). This may be because there are some cases when
feasible for any type of biochemical system (stiff, non-stiff) to capture probable states, it is important to consider the expansion cost for small tstep (time step). This may be because there are some cases when  to reach two or more different child nodes are equal or very close to each other. In addition, we intend to expand the state-space in the direction of carrying states with high probability mass. To achieve this, we treat or convert our uninformed search to an informed search infrastructure at run-time to have intuitive knowledge beyond our reach. Figure 17 shows the limits of our visibility in the state-space.
to reach two or more different child nodes are equal or very close to each other. In addition, we intend to expand the state-space in the direction of carrying states with high probability mass. To achieve this, we treat or convert our uninformed search to an informed search infrastructure at run-time to have intuitive knowledge beyond our reach. Figure 17 shows the limits of our visibility in the state-space.
Consequently, it is important to track the reactions which have high propensity function values. As it is difficult to determine the direction of the expansion, in the following section (a), we develop the post successor function on Bayes’ theorem [31, 32] to prioritize the expansion direction based only on those reactions that can be triggered at a particular time point. In sections (b) and (c), we outline the direction strategy with the depth and bounds of the expansion.
Bayesian likelihood node projection function
Bayesian methods [32, 51] are based on the principle of linking prior probability with posterior probability through Bayes’ theorem [31, 32]. Posterior probability is the improved form of prior probability, via the likelihood of finding factual support for a valid fundamental hypothesis. Therefore, we employ the standards of Bayes’ theorem to develop a function targeted to ensure the quality of the expansion based on RM reactions active in the network at any particular moment. For a concise definition for the purpose of fundamentals, refer to SI 6.
To improve the quality of expansion through a projection function, one may find it useful to remove the set of states which have low probabilities before calculating Eq. (3). However, removing these states will compromise accuracy as the step error will increase at every t. Moreover, removing these probabilities will greatly affect the solution, as defined at tf (at which a solution is required), for large dimension systems which have large state-spaces, as the step error will be much higher due to dropping probabilities without solving Eq. (3). In large systems, any species may change its behavior after a certain number of firing of reactions triggering inactive reactions in the network that will affect the probabilities of the states. If a change in behavior increases the probabilities of certain states, then removing them in an earlier stage is not wise.
Through the Bayesian Likelihood Node Projection (BLNP) function, we seek to predict the posterior probability based on the parent state’s probability and calculate the likelihood of the occurrence of reactions that will take the system from the present state to the future state. Through BLNP, we can capture knowledge about the system that will help us to make better predictions about the future state. We are also able to ensure the accuracy of the solution and an optimal domain.
It is important to decide on the direction of the expansion when choosing the future state of the system, as any reaction can occur and take the system to any new state. To understand this situation more clearly on a node level, we assume a Markov chain graph as shown in Fig. 18 of this system which has almost the same number of species count. In Fig. 19, the expansion is at intermediate position, as the initial state state(N0) = X0 is already expanded and now the expansion of state(N2) = X2 can be undertaken. To calculate the likelihood of the occurrence of reactions R1, R2, R5, we consider the propensities ai, j as a parameter. ∆ai,j depends on the kinetic parameter of the reaction. To assign weight to our belief, we deduce a function that will calculate the probability of reactions occurring and prioritize the expansion in order from reactions resulting in states with high probabilities to reaction giving states with low probabilities. It is important to note that none of the probabilities will be removed before the calculation of Eq. (5). With this function, the likelihood of occurrence of RM can be computed.
We consider each node as a junction of the prior reactions \( \left\{{R}_1^{\prime}\dots \dots .{R}_M^{\prime}\right\} \) with propensities \( \left\{{a}_{1,N}^{\prime}\dots \dots .{a}_{N\prime N}^{\prime}\right\} \) having prior likelihood values \( \left\{{b}_{1,N}^{\prime}\dots \dots .{b}_{N^{\prime },N}^{\prime}\right\} \) and future reactions {R1……. RM} with propensities {a1, N′……. aN, N′} having likelihood values {b1, N′……. bN, N′}, as given in Fig. 18.
To calculate the likelihood of the reactions, it is necessary to have prior information about the occurrence of reactions. If the expansion is to be done at the initial node state(N0) = X0 (at level 1), then the prior likelihood value \( {b}_{N,N\prime}^{\prime } \) is considered as the initial probability or as ≈1. Once the initial node has been explored, we can calculate the likelihood of the reactions inductively. To calculate the probabilities b1, N′, …. , bN, N′ of the occurrence of R1, …. , RM, we first calculate the weighted probabilities PN, 1(ω), … … .,\( {P}_{N,{N}^{\prime }}\left(\omega \right) \) of a system leaving any state by:

and multiply it with the prior probability \( {b}_{1,N}^{\prime}\dots \dots .{b}_{N^{\prime },N}^{\prime } \) of the system. This will calculate the likelihood inductively, as RM is responsible for transforming the system to the present state(Ni) = Xi at t, leading to a function,
where,
Once \( b\left({N}_{N1,.. NM}|{b}_{1,N\dots .{N}^{\prime },N}^{\prime}\right) \) is calculated for all the adjacent nodes, the values are arranged in descending order. Every value is bound to one reaction and represents the likelihood of the occurrence of the reaction that takes the system from the present node to the child nodes. Based on likelihood values (highest to lowest), the corresponding reactions are considered one by one and labelled as true events for expansion. For example, if a system has R1, R2, R3 reactions that bound to BLNP likelihood values in order from highest to lowest, respectively, then three events take the system to new state. When R1 is considered for expansion, R2 and R3 are labeled false events and R1 as the true event. When the second highest BLNP likelihood value is considered, which is for R2, then it is labeled the true event and the others, R1, R3, are labeled false events. Similarly, the last and lowest BLNP likelihood value is for R3, which is labeled as the true event and the others as false events. All states are added in the domain in order from the 1st true event to the 3rd true event. The Eq. (54) of probabilities \( b\left({N}_{N1,.. NM}|{b}_{1,N\dots .{N}^{\prime },N}^{\prime}\right) \) is what we call a BLNP function.
Figure 18 shows the Markov chain tree for selection present at level 2 (assuming that the initial node is already expanded). Here we calculate the weighted probability of a system leaving state(N2) = X2 by:
similarly, P2, 4(ω) = 0.3333 and P2, 5(ω) = 0.3418.
At level 2, the conditional probability of the occurrence of reaction R1, given the probability of occurrence of reaction R1 at level 1, is given by:
Similarly, the occurrence of reaction R1 at level 2, given the probability of occurrence of reaction R6 at level 1, is given by:
If at level 1, state(N1) = X1 and at level 2, state(N2) = X2 are explored through R1 then we say that this is a true event and temporarily consider other events false events with respect to the other reactions. Such a condition holds true for the other two cases, when, at level 1, state(N1) = X1 is explored through R1 followed by an exploration of state(N2) = X2 either by R2 or R5. Given \( {b}_{0,2}^{\prime }{\left(X-{v}_{\mu}\right)}^{\prime } \) and \( {b}_{6,2}^{\prime }{\left(X-{v}_{\mu}\right)}^{\prime } \), we calculate the likelihood of all the RM events, as given in Table 6. The likelihood values of future reactions cannot be equal, as they are based on the probabilities of occurrence of prior reactions.
From Fig. 18 and Table 6, we can infer, based on the prior reactions for RM, where M = {1, 6} that:
Case 1 (R1): At level 2, if the prior reaction is R1 and holds a true event for N0 → N2 then:
as per bN, N′ the likelihood of occurrence of reactions will be in the order R5 > R2 > R1.
Case 2 (R6): At level 2, if the prior reaction is R6 and holds a true event for N6 → N2 then
as per bN, N′ the likelihood of occurrence of reactions will be in the order R5 > R2 > R1.
There will be M number of cases (equal to elementary chemical reaction channels) if there are \( {R}_M^{\prime } \) prior reactions in the system that bring the system to the current node. The likelihood value will change based on \( {b}_{N^{\prime },N}^{\prime}\left(X-{v}_{\mu}\right)^{\prime } \). The BLNP function cannot be used standalone for expansion because it only assigns weightage to direction for expansion. In the Intelligent state projection section, we have derived the condition for our expansion strategies to work with the Markov chain graph state-space and defined the criteria for the formation of bounds (domain formed at anytime t) with time. The BLNP function (with expansion strategies), will choose the probable states in large biochemical systems where it is important to capture the moments at time t that define a system’s behavior. BLNP will be useful for identifying the most active reactions in the system while guiding the expansion towards the set of states with high probability mass.
Latitudinal search strategy
We delve deeper into the first subroutine of the ISP called the Intelligent State Projection Latitudinal Search (ISP LAS). Figure 20 manifests the infrastructure of the LAS strategy, showing Gmc, the queue and the domain. LAS’ queue data structure is based on the FIFO (First In, First Out) method. In this method, the oldest state added to the queue is considered first. We define and exploit the direction of expansion step-by-step based on intuitive knowledge (as discussed in section (a)), gained from the probability of future reaction events. We follow the conditions (as discussed in the results section). Furthermore, we show step-by-step how the nodes are explored, and states updated in the domain in Itr iterations.
At level ƌl the states are expanded only after all the states at level ƌl − 1 have been expanded; that is, the search is undertaken level-by-level and depth ƌl increases in every Itr iteration. In the case of networks with reversible reactions, the ISP condition will prevent LAS from returning to the state it came from and also prevent transitions containing cycles resulting in DAG with no repetition of any state whatsoever; however, changes in propensities ai,j are validated. Verifying the explored states in XK in iterations ensures that the algorithm completes and that a deadlock in the state transition cycles cannot occur.
The time complexity of LAS depends on the average transitioning factor Ŧ and depth ƌl and is given by (see SI 7 for detailed discussion),

where,

For the nodes at the deepest level ƌl, all walks are valid except for the very last node which stores the end state of the system. Therefore, once the end state is found, based on Eq. (20), LAS will zip \( {\mathbf{X}}_K^{\prime } \), further leaking the highest probabilities to XK for the solution of Eq. (3) which includes the end state of the system. As no state is ever repeated in the domain, space complexity will decrease when the set of states \( {\mathbf{X}}_K^{\prime } \) is bunked at t′seconds in iterations if Eqs. (19) and (20) are satisfied. In Eq. (13), \( {P}^{(t)}\left({\mathbf{X}}_K^{\prime}\right) \) is computed according to Eq. (5) (the exponential form of the CME), where τm is the tolerance and I is the identity matrix. Due to this stepping bunking of \( {\mathbf{X}}_K^{\prime } \) from XK, the time complexity O(Ŧd + 1) reduces to  , where |XJ| is the size of the state-space [13]. In contrast, the expansion of new nodes carrying similar states tend to increase
, where |XJ| is the size of the state-space [13]. In contrast, the expansion of new nodes carrying similar states tend to increase  however, repetitive states are ignored.
however, repetitive states are ignored.
If the input τm is too small, the algorithm automatically uses the default value of sqrt(eps). Here sqrt is the square root and eps is the default value of the epsilon on machine. The expansion of child nodes containing state(Ni) = Xi stops if the condition of Eq. (32) is not satisfied. If the criterion of slow and fast reaction [12] is considered, then the condition of Eq. (31) or (32) is used, depending on the number of RM(sr) and RM(fs). Table 7 shows the steps of the LAS method with the embedded BLNP function, from steps 4a to 5b.
LAS will be optimal if the transitions between all the states are uniform; that is, all the RM reactions have the same propensity values. However, in real biochemical models, this condition is unusual. To see a step-by-step demonstration of the ISP LAS algorithm on a toy model, refer to SI 2. We now turn our attention to the second variant of the ISP. We apply the method to a toy model to see how it differs from LAS.
Longitudinal-latitudinal search strategy
Here, we delve deeper into the second sub-routine of ISP called the Intelligent State Projection Longitudinal Latitudinal Search (ISP LOLAS). Figure 21 visually represents the infrastructure of the LOLAS strategy, showing the Gmc, stack and the domain. The stack data structure of LOLAS is based on the LIFO (Last In, First Out) method. In this method, the newest state added to the stack is considered first. In particular, we define the bound limit and exploit the direction of the expansion step-by-step based on intuitive knowledge (as discussed in section (a)), gained from the probability of future reaction events and follow the conditions (as discussed in the Results section). Furthermore, we show step-by-step how nodes carrying states are explored in a bidirectional way and how these states were updated in the domain in Itr iterations.
The states at level ƌl are expanded only after the neighboring states at level ƌl − 1 have been expanded for RM: that is, the search is undertaken level-by-level. Depth ƌl increases in the same Itr iteration up to a certain ƃlimit (bound limit). The expansion limit is set by ƃlimit, ƌstep (depth step). In contrast to LAS, it is not set by depth ƌl,. The LOLAS search updates the dictionary Dict of Gmc by the stoichiometric vector function, vμ(X(t)) on state at level ƌl to explore the child nodes carrying states on levels ƌl + 1, ƌl + 2 … .. ƌl + l, where l = {1, 2…. ∞} and then retracts to level ƌl at which new state exploration decisions can be made. In the case of networks with reversible reactions, the ISP conditions will prevent LOLAS from returning to the state it came from and prevent transitions containing cycles resulting in DAG with no repetition of any state whatsoever; however, the change in propensities ai, j is validated. Verifying the explored states in XK in iterations ensures that the algorithm completes and that deadlocks in the state transition cycles cannot occur.
In the absence of ƃlimit, the algorithm will not retract. It will explore longitudinally by tracking only one RM reaction. In addition, the algorithm will not terminate with an optimal order domain carrying a maximum probability mass. This would lead to an increase in the approximation error. Instead, it will terminate when carrying only those set of states as a result of tracking only a few RM, creating an insufficient domain for approximation. Therefore, by default, the value of ƃlimit ≥ 1 is kept for large systems and can be increased depending upon the model’s dimension and the availability of the testing environment’s random access memory (RAM). LOLAS’ worst-case time complexity depends on the average transitioning factor Ŧ. Depth ƌl is given by (see SI 7 for a detailed discussion):

LOLAS only stores the transition path to the end state besides the neighbors of each relevant node in the exploration. Once all descendants are updated with the relevant propensities in the projection, it discards the node from the domain (explored), making it ready for the approximation. LOLAS first considers the R1 reaction and the corresponding stoichiometric vector v1 of the system, to explore all the neighboring states up to bound limit ƃlimit. It then considers R2, R3, … ..,RM for the same ƃlimit and the corresponding v2, v3, … .. , vM to explore the states. For count(ƃlimit), LOLAS retracts to the R1 reaction and explores the new neighboring states longitudinally. It then reconsiders R2, R3, … .. , RM to explore the other states in a similar fashion. Provided with this reaction tracking pattern, the BLNP function alters this trend and guides this tracking by considering reactions in a different order based on their propensities and the number of probable states of the system.
If the system is ending in a set of state XK carried by nK at tf, then LOLAS will explore the states efficiently, as long as count(ƃlimit) ≤ ƃlimit, otherwise count(ƃlimit) is reset for further expansion. Choosing the appropriate ƌlimit and ƃstep depends on the type of biochemical reaction network and the computing configuration. Starting with a depth 1 → ƃlimit, LOLAS explores all the states until they return null. It then resets the count(ƃlimit) and retracts to explore again. In most cases, fewer states are positioned at the lower level. They increase at a higher level when the number of active RM reactions increases, so retracting provides the ability to track all the reactions simultaneously. The nature of the LOLAS expansion means that it is able to find more states at any time t compared to LAS. It is also able to find them at the deepest level of the graph. The states at depth ƌl are explored once, the states at depth ƌl − 1 are explored twice, states at depth ƌl − 2 are explored three times and so on, until it has explored all the system’s states. If the input τm is too small, the algorithm automatically uses the default value of sqrt(eps). Here sqrt is the square root and eps is the default value of the epsilon on machine. The expansion of the child nodes containing state(Ni) = Xi stops if the condition of Eq. (32) is not satisfied. If the slow and fast [12] reaction criterion is considered, then either Eq. (31) or (32) conditions are used depending on the number of RM(sr) and RM(fs). Table 8 shows the LOLAS method, with an embedded BLNP function from steps 4a to 5b.
Refer to SI 3 for the step-by-step demonstration of the ISP LOLAS algorithm, where we assume the same toy model system.
Availability of data and materials
All the result data files generated and analyzed during the current study are available in the “isp” repository of https://github.com/rkosarwal/isp. Codes are not publicly available due to search engine privacy but are available from the corresponding or first author on reasonable request.
Abbreviations
- ai,j or aμ :
-
Propensity of chemical reaction
- ∆a i,j :
-
Change in propensity
- \( {\boldsymbol{a}}_{\mathbf{1},\boldsymbol{N}\prime}^{\prime } \), … .,\( {\boldsymbol{a}}_{\boldsymbol{N},\boldsymbol{N}\prime}^{\prime } \) :
-
Propensities of the prior reactions
- a fr :
-
Probability of a jump process from state Xi − 1 to Xi per unit time
- a rv :
-
Probability of a jump process from state Xi to Xi − 1 per unit time
- A or Ai,j :
-
Defines the transition between i, j and its weightage
- ƃ limit :
-
Exploration bound limit in LOLAS
- \( {\boldsymbol{b}}_{{\boldsymbol{N}}^{\prime },\boldsymbol{N}}^{\prime}\left(\boldsymbol{X}-{\boldsymbol{v}}_{\boldsymbol{\mu}}\right)^{\prime } \) :
-
Prior Bayesian likelihood values {\( {b}_{1,N}^{\prime },\dots \dots {b}_{N^{\prime },N}^{\prime } \)}
- \( \boldsymbol{b}\left({\boldsymbol{N}}_{\boldsymbol{N}\mathbf{1},..\boldsymbol{N}\boldsymbol{M}}|{\boldsymbol{b}}_{\mathbf{1},\boldsymbol{N}\dots .{\boldsymbol{N}}^{\prime },\boldsymbol{N}}^{\prime}\right) \) :
-
Represents Bayesian likelihood value given prior \( {b}_{N^{\prime },N}^{\prime } \)
- Boundlower or BoundL :
-
Define the set of states {X1, 2……S, b1, 2, 3, …. limit} at ƃlimit already present in the domain for current iteration
- Boundupper or BoundU :
-
Define the set of states {X1, 2……S, b1, 2, 3, …. limit} at ƃlimit added in the domain at the end of current iteration
- c, c1, c2 :
-
Constants
-
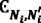 :
: -
Total transition/walk cost from node Ni to \( {N}_i^{\prime } \)
- Dict :
-
Dictionary of the model having transition records
- ƌ l :
-
Exploration depth limit in LAS
- ƌ step :
-
Exploration depth step in ISP
- dim :
-
Dimension of sub-matrix in Sliding Windows Method
- domain :
-
Defines the set of states of domain in current iteration that forms Boundupper
- domain previous :
-
Defines the set of states of domain in previous iteration that forms Boundlower
- D j :
-
Diagonal matrix whose diagonal entries are one
- e :
-
Markov chain tree edge, representing walk from Ni to \( {N}_i^{\prime } \)
- e 1 :
-
First unit basis vector in Krylov Subspace Method
- e rror :
-
Represents error value in calculation
- exp():
-
Exponential function
- eps :
-
Epsilon
- Έ y :
-
Denote the sequence of events Έ1, Έ2… .,
- f(y):
-
Represents the positive real value function of y
- G mc :
-
Represents graph associated with the Markov chain tree
- \( {\overline{\boldsymbol{H}}}_{\boldsymbol{dim}} \) :
-
Upper matrix (Hessenberg Matrix)
- I T :
-
Identity matrix I = diag (1, 1, …..1)T
- I tr :
-
Denote the iterations in ISP
- k M :
-
Kinetic parameter of the chemical reaction where M = {1, 2…. ∞}
- l :
-
Used as subscript for length of depth, for example ƌl
- n J :
-
Set of nodes as {\( {N}_1,{N}_2,\dots \dots .{N}_{S^{\widetilde{\mathrm{N}}}} \)}
- n K :
-
Set of nodes carrying set of XK at any iteration
- \( {\mathbf{n}}_{\boldsymbol{K}}^{\prime } \) :
-
Set of nodes carrying set of \( {\mathbf{X}}_K^{\prime } \) at any iteration
- N 0 :
-
Root node carrying initial state X0
- Ni or Ni :
-
Any node
- \( \widetilde{\mathbf{N}} \) or \( \left\{{\mathbf{S}}_{\mathbf{1}},\dots \dots .{\mathbf{S}}_{\widetilde{\mathbf{N}}}\right\} \) :
-
Number of different species
- num1, num2 :
-
Random number generated by uniform random number generator (URN)
- \( {\boldsymbol{P}}^{\left({\boldsymbol{t}}_{\mathbf{0}}\right)}\left({\boldsymbol{X}}_{\mathbf{0}}\right) \) :
-
Initial probability at t = 0
- P(t)(XK):
-
Probability of set of states at time t
- \( {\boldsymbol{P}}_{\boldsymbol{N},{\boldsymbol{N}}^{\prime }}\left(\boldsymbol{\omega} \right) \) :
-
Weighted probability of transition from Ni to \( {N}_i^{\prime } \)
- R M :
-
M elementary chemical reaction channels {R1, R2……. RM}
- \( {\boldsymbol{R}}_{\boldsymbol{M}}^{\prime } \) :
-
Prior M elementary chemical reaction channels \( \left\{{R}_1^{\prime },{R}_2^{\prime}\dots \dots .{R}_M^{\prime}\right\} \)
- R M(fs) :
-
M elementary chemical reaction channels of fast reactions
- R M(sr) :
-
M elementary chemical reaction channels of fast reactions
-
 tract
:
tract
: -
Number of retractions in LOLAS
- \( {\mathbf{S}}^{\widetilde{\mathbf{N}}} \) :
-
Approximate number of states
- \( \hat{\boldsymbol{S}} \) :
-
Number of stages in expansion {1, 2, …….}
- SI:
-
Supporting information
- S uc :
-
Implicit successor or operator
- sqrt :
-
Square root
- t 0 :
-
Time at which initial conditions of system are defined
- t ′ :
-
Time at which \( {\mathbf{X}}_K^{\prime } \) is dropped from the domain
- t :
-
Any random time in seconds
- t d :
-
Time at which XK is updated in the iteration
- t f :
-
Final time at which solution is required
- Ŧ :
-
Transitioning factor
- \( {\boldsymbol{U}}_{{\boldsymbol{X}}_{\boldsymbol{i}},{\boldsymbol{X}}_{{\boldsymbol{i}}^{\prime }}} \) :
-
Set of all arborescences
- ∣U∣:
-
Define the cardinality of any set
- v :
-
Krylov Sub-space method - A column vector of a length equal to the number of different species present in the system
- vμ or vM :
-
Stoichiometric vector represents the change in the molecular population of the chemical species by the occurrence of one RM reaction. It also defines the transition from state Xi to \( {X}_{i^{\prime }} \) in the Markov chain tree
- vμ(X(t)) or vM(X(t)):
-
Stoichiometric vector function, where X is any random state
- vμ or vM :
-
Matrix of all the Stoichiometric vectors [v1; v2; ……vμ]
- W y :
-
Probability that is computed inductively by W(0) = P(0) in uniformization method
- \( {\mathbf{x}}_{\mathbf{1}},\dots \dots .{\mathbf{x}}_{\widetilde{\mathbf{N}}} \) :
-
Number of counts of different species
- X or Xi or \( {\boldsymbol{X}}_{{\boldsymbol{i}}^{\prime }} \) :
-
Any random state
- X 0 :
-
Initial state or initial condition
- X J :
-
Ordered set of possible states \( \left\{{X}_1,\dots \dots .{X}_{S^{\widetilde{N}}}\right\} \) of the system
- X K :
-
Set of new states or domain at any iteration
- \( {\mathbf{X}}_{\boldsymbol{K}}^{\prime } \) :
-
Set of states dropped from domain at t′ at any iteration
- y, y0 :
-
Positive integers
- Y y :
-
Poisson process given that 0 < y ≤ M
- Z :
-
Number of bounds in ISP
- τm or tolm :
-
Tolerance value
- τm(leak):
-
\( {P}^{(t)}\left({\mathbf{X}}_K^{\prime}\right) \) leakage point
- Ӕ:
-
Approximate solution of the CME
- ω :
-
Weight or cost of single transition from Xi to \( {X}_{i^{\prime }} \). It is equivalent to ai,j
- Ѫ c :
-
Markov chain representing biochemical process
- Ѭ:
-
Markov chain tree with nJ
- λt :
-
Uniformization rate
-
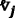 :
: -
Number of nonzero elements in Pj
- φ :
-
Sample space
- Ω :
-
Asymptotic lower bound
- O :
-
Asymptotic upper bound
- Θ :
-
Asymptotic tight bound
- {1, 2…….K}:
-
Indexing of set of states and set of nodes
- μ = {1, 2, ….M}:
-
Channels of chemical reaction propensity
References
Roberts RM, Cleland TJ, Gray PC, Ambrosiano JJ. Hidden Markov model for competitive binding and chain elongation. J Phys Chem B. 2004;108(20):6228–32.
Kholodenko BN. Negative feedback and ultrasensitivity can bring about oscillations in the mitogen-activated protein kinase cascades. Eur J Biochem. 2000;267(6):1583–8. https://doi.org/10.1046/j.1432-1327.2000.01197.x.
Ozer M, Uzuntarla M, Perc M, Graham LJ. Spike latency and jitter of neuronal membrane patches with stochastic Hodgkin–Huxley channels. J Theor Biol. 2009;261(1):83–92.
Murray JM, Fanning GC, Macpherson JL, Evans LA, Pond SM, Symonds GP. Mathematical modelling of the impact of haematopoietic stem cell-delivered gene therapy for HIV. J Gene Med. 2009;11(12):1077–86. https://doi.org/10.1002/jgm.1401.
Hogervorst E, Bandelow S, Combrinck M, Irani SR, Smith AD. The validity and reliability of 6 sets of clinical criteria to classify Alzheimer’s disease and vascular dementia in cases confirmed post-mortem: added value of a decision tree approach. Dement Geriatr Cogn Disord. 2003;16(3):170–80.
Schulze J, Sonnenborn U. Yeasts in the gut. Dtsch Aerzteblatt Online. 2009. https://doi.org/10.3238/arztebl.2009.0837.
Zhou Y, Hou Y, Shen J, Huang Y, Martin W, Cheng F. Network-based drug repurposing for novel coronavirus 2019-nCoV/SARS-CoV-2. Cell Discov. 2020;6(1). https://doi.org/10.1038/s41421-020-0153-3.
Gillespie DT. A rigorous derivation of the chemical master equation. Phys A Stat Mech its Appl. 1992;188(1–3):404–25.
Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81(1):2340–61. https://doi.org/10.1063/1.2710253.
Weber R. Markov chains. 2011. http://www.statslab.cam.ac.uk/~rrw1/markov/M.pdf. Accessed 22 Nov 2016.
Goutsias J, Jenkinson G. Markovian dynamics on complex reaction networks. Phys Rep. 2013;21218(2):199–264. https://doi.org/10.1016/j.physrep.2013.03.004.
Goutsias J. Quasiequilibrium approximation of fast reaction kinetics in stochastic biochemical systems. J Chem Phys. 2005;122(18):1–15.
Burrage K, Hegland M, Macnamara S, Sidje R. A Krylov-based finite state projection algorithm for solving the chemical master equation arising in the discrete modelling of biological systems. Proc Markov Anniv Meet. 2006:1–18.
Jones MT. Estimating Markov transition matrices using proportions data: an application to credit risk. IMF Work Pap. 2005;05(219):1. https://doi.org/10.5089/9781451862386.001.
Gillespie DT. Markov processes - an introduction for physical scientists. Cambridge: Elsevier; 1992. p. 592.
Mouroutsos SG, Sparis PD. Taylor series approach to system identification, analysis and optimal control. J Franklin Inst. 1985;319(3):359–71. https://doi.org/10.1016/0016-0032(85)90056-0 Cited 2018 Jul 12.
Eslahchi MR, Dehghan M. Application of Taylor series in obtaining the orthogonal operational matrix. Comput Math with Appl. 2011;61(9):2596–604.
Wolf V, Goel R, Mateescu M, Henzinger T. Solving the chemical master equation using sliding windows. BMC Syst Biol. 2010;4(1):42. https://doi.org/10.1186/1752-0509-4-42.
Sidje RB, Vo HD. Solving the chemical master equation by a fast adaptive finite state projection based on the stochastic simulation algorithm. Math Biosci. 2015;269:10–6.
Sunkara V, Hegland M. An optimal finite state projection method. Procedia Comput Sci. 2010;1(1):1579–86. https://doi.org/10.1016/j.procs.2010.04.177.
Munsky B, Khammash M. The finite state projection algorithm for the solution of the chemical master equation. J Chem Phys. 2006;124(4):1–13.
Mikeev L, Sandmann W, Wolf V. Numerical approximation of rare event probabilities in biochemically reacting systems. Lect Notes Comput Sci (including Subser Lect Notes Artif Intell Lect Notes Bioinformatics). 2013;8130 LNBI:5–18.
MacNamara S, Bersani AM, Burrage K, Sidje RB. Stochastic chemical kinetics and the total quasi-steady-state assumption: application to the stochastic simulation algorithm and chemical master equation. J Chem Phys. 2008;129(9):095105.
Dinh KN, Sidje RB. An application of the Krylov-FSP-SSA method to parameter fitting with maximum likelihood. Phys Biol. 2017;14(6):065001. https://doi.org/10.1088/1478-3975/aa868a.
Harrison RL, Granja C, Leroy C. Introduction to Monte Carlo simulation; 2010. p. 17–21. https://doi.org/10.1063/1.3295638.
Dinh KN, Sidje RB. Understanding the finite state projection and related methods for solving the chemical master equation. Phys Biol. 2016;13(3):035003.
Munsky B, Khammash M. A multiple time interval finite state projection algorithm for the solution to the chemical master equation. J Comput Phys. 2007;226(1):818–35.
Sunkara V. Analysis and numerics of the chemical master equation. 2013. http://www.math.kit.edu/ianm3/~sunkara/media/thesis_sunkara.pdf. Accessed 25 May 2018.
Padgett JMA, Ilie S. An adaptive tau-leaping method for stochastic simulations of reaction-diffusion systems. AIP Adv. 2016;6(3):035217.
Cao Y, Gillespie DT, Petzold LR. Efficient step size selection for the tau-leaping simulation method. J Chem Phys. 2006;124(4):1–11.
Schlecht V. How to predict preferences for new items. Invest Manag Financ Innov. 2014;5(4):7–24.
Fahidy TZ. Some applications of Bayes’ rule in probability theory to electrocatalytic reaction engineering. Int J Electrochem. 2011;2011(1):1–5. https://doi.org/10.4061/2011/404605.
Anantharam V, Tsoucas P. A proof of the Markov chain tree theorem. Stat Probab Lett. 1989;8(2):189–92. https://doi.org/10.1016/0167-7152(89)90016-3 Cited 2018 May 15.
Aldous D. The Continuum random tree II: an overview. In: Barlow MT, Bingham NH, editors. Stochastic analysis. Cambridge: Cambridge University Press; 1992.
Diaconis P, Efron B. Markov chains indexed by trees. Ann Stat. 1985;13(3):845–74.
Gursoy BB, Kirkland S, Mason O, Sergeev S. On the markov chain tree theorem in the max algebra. Electron J Linear Algebr. 2012;26(12):15–27.
Mastny EA, Haseltine EL, Rawlings JB. Two classes of quasi-steady-state model reductions for stochastic kinetics. J Chem Phys. 2007;127(9). https://doi.org/10.1063/1.2764480.
Ling H, Kulasiri D, Samarasinghe S. Robustness of G1/S checkpoint pathways in cell cycle regulation based on probability of DNA-damaged cells passing as healthy cells. BioSystems. 2010;101(3):213–21. https://doi.org/10.1016/j.biosystems.2010.07.005.
MacNamara S, Burrage K. Krylov and steady-state techniques for the solution of the chemical master equation for the mitogen-activated protein kinase cascade. Numer Algorithms. 2009;51(3):281–307. https://doi.org/10.1007/s11075-008-9239-y.
Jahnke T, Huisinga W. A dynamical low-rank approach to the chemical master equation. Bull Math Biol. 2008;70(8):2283–302. https://doi.org/10.1007/s11538-008-9346-x.
Hegland M, Hellander A, Lötstedt P. Sparse grids and hybrid methods for the chemical master equation. BIT Numer Math. 2008;48(2):265–83. https://doi.org/10.1007/s10543-008-0174-z.
DeVore RA. Nonlinear approximation. Acta Numer. 1998;7:51–150. https://doi.org/10.1017/S0962492900002816.
DeVore RA, Howard R, Micchelli C. Optimal nonlinear approximation. Manuscripta Math. 1989;63(4):469–78. https://doi.org/10.1007/BF01171759.
Chijindu EVC. Search in artificial intelligence problem solving. IEEE: African Journal of Computing & ICT. 2012;5(5):37–42.
Barr A, Feigenbaum E. The handbook of artificial intelligence vol I. Math Soc Sci. 1983;4:320–4.
Korf RE. Artificial intelligence search algorithms. In: Algorithms Theory Comput Handb; 1996.
Korf RE. Depth-first iterative-deepening. An optimal admissible tree search. Artif Intell. 1985;27(1):97–109.
Rudowsky I. Intelligent agents. Commun Assoc Inf Syst. 2004;14(August):275–90.
Lawlor OS. In-memory data compression for sparse matrices. In: Proc 3rd Work Irregul Appl Archit Algorithms, vol. 6; 2013. p. 1–6. https://doi.org/10.1145/2535753.2535758.
Koza Z, Matyka M, Szkoda S, Mirosław Ł. Compressed multi-row storage format for sparse matrices on graphics processing units; 2012. p. 1–26. https://doi.org/10.1137/120900216.
Manoukian EB. Modern concepts and theorems of mathematical statistics. New York: Springer New York; 1986. (Springer Series in Statistics). https://doi.org/10.1007/978-1-4612-4856-9.
Acknowledgements
RK acknowledges the project funding and necessary resourcing received from Lincoln University, New Zealand for the duration of three years.
Funding
RK acknowledges the writing scholarship received from AgLS Faculty, Lincoln University, New Zealand to write this paper for a month (NZD2000). Only obligation is to submit a paper to a journal.
Author information
Authors and Affiliations
Contributions
RK and DK developed the research questions and designed the research. RK developed and implemented the algorithm; DK and SS directed the project, RK and DK wrote the manuscript and SS independently critiqued the manuscript, which has been read, improved, and approved by all three authors.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
Not applicable.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated in a credit line to the data.
About this article
Cite this article
Kosarwal, R., Kulasiri, D. & Samarasinghe, S. Novel domain expansion methods to improve the computational efficiency of the Chemical Master Equation solution for large biological networks. BMC Bioinformatics 21, 515 (2020). https://doi.org/10.1186/s12859-020-03668-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12859-020-03668-2








 shows the increase in the domain size with the states’ populations.
shows the increase in the domain size with the states’ populations.  shows the point in time where new set of states are explored and updated in the domain
shows the point in time where new set of states are explored and updated in the domain

 shows the increase in the domain size with the states’ populations.
shows the increase in the domain size with the states’ populations.  shows the point in time where new set of states are explored and updated in the domain
shows the point in time where new set of states are explored and updated in the domain






 is the initial node and
is the initial node and  are nodes that are directly reachable from the initial node when exactly one RM occurs. When a further RM occur, the system jumps to other
are nodes that are directly reachable from the initial node when exactly one RM occurs. When a further RM occur, the system jumps to other  nodes
nodes



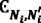 :
: tract
:
tract
: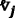 :
: