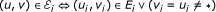- Research article
- Open access
- Published:
Bacterial syntenies: an exact approach with gene quorum
BMC Bioinformatics volume 12, Article number: 193 (2011)
Abstract
Background
The automatic identification of syntenies across multiple species is a key step in comparative genomics that helps biologists shed light both on evolutionary and functional problems.
Results
In this paper, we present a versatile tool to extract all syntenies from multiple bacterial species based on a clear-cut and very flexible definition of the synteny blocks that allows for gene quorum, partial gene correspondence, gaps, and a partial or total conservation of the gene order.
Conclusions
We apply this tool to two different kinds of studies. The first one is a search for functional gene associations. In this context, we compare our tool to a widely used heuristic - I-ADHO RE - and show that at least up to ten genomes, the problem remains tractable with our exact definition and algorithm. The second application is linked to evolutionary studies: we verify in a multiple alignment setting that pairs of orthologs in synteny are more conserved than pairs outside, thus extending a previous pairwise study. We then show that this observation is in fact a function of the size of the synteny: the larger the block of synteny is, the more conserved the genes are.
Background
The increasing number of fully sequenced microbial genomes (more than 1200 genomes are now completed and available) is fuelling our knowledge on the architecture and dynamics of these bacterial genomes [1]. In this context, the identification of conserved genomic regions across several species is of prime importance. These conserved blocks of genes are referred to in the literature as (micro-)syntenies, (conserved) synteny blocks, (conserved) gene clusters, or gene teams. From an evolutionary stand-point, they are important for understanding how, as species diverge, their gene order is progressively shuffled [2, 3]. From a more practical genome annotation perspective, it is also important to identify which regions are resisting this continuous shuffling because these regions are likely to be subjected to stronger functional constraints. In prokaryotic genomes these constraints are of course related to the operon structure. Operons, although subjected as well to gene shuffling [4] appear to be more robust, especially in the case of physically interacting gene products [5].
In recent years, various computational methods have been proposed to identify syntenies by comparison of two or more genomes. In the following, we shall focus on methods working at the gene level, i.e. excluding approaches based on other genetic markers. Even with this restriction, the approaches vary greatly from one study to the other. However, they could be roughly classified into several categories according to their ultimate goal, the algorithmic technique used to solve the problem and the type of constraints they can handle. Among these constraints, the most discriminant ones are i) whether the gene-to-gene (homology) relationship is one-to-one, many-to-many or is an equivalence relation; ii) whether the model accounts for inversions or iii) insertion/deletion events (duplication events are already covered by criterion i), iv) whether the approach is pairwise or is applicable to multiple genomes. Table 1 summarises some important cases found in the literature that can be classified in three main categories.
The first category contains methods that aim at reconstructing evolutionary scenarios using sorting by reversal to recover the minimal number of permutations needed to transform one genome (modelled as a signed or unsigned permutation of integers) into the other. In such approaches, of which the two main ones are GRIMM [6] and CINTENY[7], the identification of blocks of syntenies is, in some way, a by-product of the algorithm, not its main goal. Some authors also formalise the problem of genome alignment as an exact search for common intervals between permutations. The first article using this formalism was Uno et al. [8]. Two important extensions were proposed later on, an extension to multiple alignment by Hebert and Stoye [9] and another extension to a many-to-many relation by Didier et al. [10].
A second, different, formalism used by several authors is well illustrated by the concept of GENE TEAMS[11], proposed originally by Bergeron et al. This defines syntenies as sets of genes such that on each genome no pair of genes from the team are separated by more than delta genes, the main limitation being that, in the original formulation, the homology relation is supposed to be one-to-one.
This idea was developed in several papers, He and Goldwasser [12] proposed the notion of HOMOLOGY TEAMS, which allows duplications on a genome; Pasek et al. [13] chose to cut the genes into protein domains to force an equivalence relation. Some other extensions of the model were suggested by Kim et al. (relaxing the proximity constraint on several genomes [14]), and Ling et al. (allowing for overlapping units, for example sequence anchors: [15, 16]). More generally these approaches consider the question of finding syntenies as a problem of combinatorial optimisation and often rely on graph theory both to formalise and to solve it. The main difficulty is to limit the combinatorial explosion when the gene-to-gene relationship is not one-to-one. The common components approach proposed by Boyer et al. [17] in a more general biological context belongs to the same family. The approach developed in this paper is an extension of this latter method and will therefore be detailed later on.
In a third category of methods, the problem of genome alignment is treated in a similar way as what is done more classically for pairwise or multiple sequence alignments and relies on a dynamic programming approach to solve it. Three typical examples of such an approach are FISH [18], DAGCHAINER[19] and COLINEAR SCAN[20]. The two strong advantages brought by these approaches are i) they do not require an explicit gene-to-gene relationship and can cope with an arbitrary similarity (i.e. substitution) score between genes; ii) as score-based techniques they are more amenable to a statistical evaluation of the significance of the predicted regions. On the other hand, the most important difficulty is to handle inversions in the dynamic programming framework.
Of course, this classification is not perfect and several hybrid methods have already been proposed that belong to several classes. For instance, SYNTENATOR[21] (and its most recent version CYNTENATOR[22]) uses both dynamic programming and a partial order graph representation to detect conserved gene orders in multiple genomes.
In this paper, we introduce an extension of the general graph alignment algorithm presented in [17] and [23] successively. In [17] we introduced the idea of a merged representation of a graph alignment as a multigraph (termed Network Alignment Multigraph (NAM)). This corresponds to an idea that was previously more informally stated in [24] and was also developed in [25]. The definition of blocks of synteny (allowing for gene gaps and permutations) then follows from simple properties of this multigraph. This first approach however suffered from two limitations: i) it required the explicit construction of the NAM, therefore facing the problem of combinatorial explosion in case of multiple genomes or of a very degenerated gene-to-gene relationship and ii) it assumed that genes are in correspondence when they form a clique (i.e. are all pairwise related). In [23] we proposed, in the context of protein-protein-interaction (PPI) networks, to address the first issue by a more careful exploration of the search space, using a depth-first search and "on-the-fly" construction of the NAM. We also introduced alternative ways of grouping genes such as stars or, simply, as connected components instead of as complete cliques. In this paper, we increase the flexibility even more by introducing a quorum i.e., when dealing with multiple (n > 2) genomes, we do not require genes to be present on all but only on at least q (≤ n) of them. Notice that the algorithm presented in [23] is not restricted to genomes but applies to any kind of graphs. Our extension will apply as well in the general case. In this paper, we shall therefore keep all definitions as general as possible but restrict the illustrations and interpretations to the case of linear graphs representing genomes.
This paper is organised as follows. First, we describe the approach, starting with an informal presentation before going through the definitions, stating precisely what objects we are going to look for, and then what algorithm we are going to use. In the next section, we describe our results, a comparison to an existing method called I-ADHO RE[26], and an illustration of the interest of the approach for studies on bacterial evolution.
Description of the approach
Informal presentation of the approach
In this section, we first give a brief summary of the approach without quorum, then explain informally how to introduce it.
Given n chromosomes represented as interval graphs (i.e. vertices are genes and two genes are connected when they are adjacent on the chromosome, or, more generally, when there are less than δ gap intervening genes between them), the first step is to define a pairwise correspondence relation (noted S) between genes from different chromosomes. Ideally S could be homology (i.e. having a common ancestor) or isofunctionality (i.e. having the same function). In practice, both are traditionally approximated by sequence similarity, for instance by thresholding a BLASTP score or using more sophisticated orthologs detection techniques [27, 28]. Note that, by contrast to homology and isofunctionality that are both transitive, thresholded sequence similarity and orthology are not necessarily transitive relations.
With this pairwise gene-to-gene correspondence at hand, the next step is to extend it to a multiple (n-way) correspondence. This is done by specifying a topology constraint on S. The strongest constraint is that genes connected by S form a clique [17] and the loosest constraint is that they merely form a connected component. Intermediate constraints, such as quasi-cliques are also possible [23]. Whatever the choice of this constraint, we end up with n-tuples of genes representing the n-way gene correspondence between the n genomes.
These n-tuples - also called "spines" [25] - constitute the vertices of a graph representation called Network Alignment Multigraph (NAM). These vertices are connected by n sets of edges - also called "colours" - corresponding each to the connectivity in a primary interval graph. Figure 1 gives an example of a NAM for three genomes where the spines are defined as cliques of the correspondence relation S.
Example of Network Alignment Multigraph. A simple example of layered data graph (top) and network alignment multigraph NAM (bottom). The layered data graph represents three genomes (blue, red and green). Vertices represent genes and coloured edges represent strict gene adjacency along each genome (no gaps edges in this example). The inter-genomic gene-to-gene correspondence relation S is represented by black dotted edges (notice that S is neither one-to-one nor transitive). If we choose to associate genes that form cliques of S (other choices are possible, see text), then the corresponding network alignment multigraph (NAM) is displayed on the bottom. The vertices of the NAM are 3 - uples (cliques) of genes, also called spines. The coloured edges between spines correspond to the original edges in the layered data graph. For instance, (a1, a2, a3) is red-connected to (b1, b2, b3) because a2 is connected to b2 in the red layer of the layered data graph. The same is true for (b1, b2, b3) and (c1, c2, c3) since b2 and c2 are connected in the red layer. Conversely, (a1, a2, a3) is not blue-connected to (b1, b2, b3) since there is one gap gene (d1) on the blue genome separating a1 from b1 (see text on how to introduce gaps). Syntons are the sets of spines that are connected for all colours. They form a partition of the PNAM vertices. In this case there are 2 syntons: {(a1, a2, a3)} and {(b1, a2, a3), (b1, b2, b3), (c1, c2, c3)}.
In this NAM, we then simply define blocks of syntenies -called syntons- as the maximal subgraphs that are connected on each of the n colours.
This definition of syntenies matches the intuition that they are made of corresponding neighbourhoods: the selection of spines ensures the gene-to-gene correspondence, and the connectivity condition on each colour ensures that on every genome a synton involves connected genes. Also notice that this definition allows for any permutation in the gene order along the chromosomes.
An important property that follows from this definition is that syntons form a partition of the vertices of the NAM. This means that efficient partitioning algorithms can be put into play, provided that the NAM has been already built.
But therein lies the rub: in the general case, the NAM itself may grow exponentially with the number of genomes, both in terms of vertices and of edges.
In Deniélou et al. [23] we proposed to avoid the explicit construction of the NAM by building "on the fly" only the parts of the multigraph we need. The idea is to add the genomes progressively in a depth-first search (and construction) of the multigraph. To do this, we basically alternate two procedures: Split and Expand. Split partitions the current multigraph on the previously treated genomes and Expands adds a new genome.
In this paper, we show that the same kind of strategy also works when allowing for missing genes on several genomes.
The basic idea is that instead of n-tuples we now allow for k-tuples, with 2 ≤ q ≤ k ≤ n, where q is a quorum fixed by the user. With these k-tuples, we can define a Partial Network Alignment Multigraph (PNAM) in a similar way as we defined the NAM before, and syntons are maximal subsets of k-tuples that are connected on the k colours.
Intuitively, this means that a synton concerns exactly k genomes (with q ≤ k ≤ n). On these genomes, a synton is made of corresponding neighbourhoods as with the previous definition and the n - k remaining genomes are simply ignored.
The next sections explain the formalisation and algorithm in more detail.
Layered data graph
The layered data graph (also called layered alignment graph in [25]) provides the simplest representation of the primary data at hand.
Definition . (adapted from [25]) Given a set of n primary graphs G i = (V i , E i ), i ∈ [|1, n|] and a correspondence relation S between the elements of distinct sets V i , the layered data graph is the graph D = (V, E) with
Observe that there are two kinds of edges in E: edges in E P correspond to the original sets E i (here-after called intra-layer edges) and the other ones (E S ) connect vertices from different layers (here-after called inter-layer edges) (see Figure 1).
In the specific case of genomes, V i represents the set of genes in the ith genome and E i represents gene contiguity: (u i , v i ) ∈ E i ⇔ |rank(u i ) - rank(v i )| ≤ δ gap where rank is the rank of the gene on the chromosome and δ gap is a gap parameter (the formula can easily be adapted to circular genomes as well).
n-way partial correspondence and don't care element
As mentioned earlier, dealing with n ≥ 2 genomes requires to define formerly how genes from different genomes are aggregated.
The definition of an n-correspondence without a quorum (i.e. for q = n) is the following:
Definition (without quorum). An n-way correspondence between elements of V1, V2,..., V
n
is defined as a restriction of the cartesian product, denoted by
of the cartesian product, denoted by .
.
Several practical cases of such an aggregation are discussed in [23].
For instance, a clique aggregation requires that all elements of an n-tuple are pairwise related:  , viS v
j
.
, viS v
j
.
Conceptually the introduction of a quorum q consists of working with k-tuples of genes (with q ≤ k ≤ n) instead of n-tuples. However for the sake of simplicity, we shall continue to work with n-tuples by introducing a don't care element, *.
Given  , we introduce a function called cover which for a given n-tuple v returns the set of nodes in v that are not don't care elements. Formally,
, we introduce a function called cover which for a given n-tuple v returns the set of nodes in v that are not don't care elements. Formally,  , cover(v) = {v
i
≠ *, i ∈ [|1, n|]}.
, cover(v) = {v
i
≠ *, i ∈ [|1, n|]}.
One can now define an n-way partial correspondence.
Definition (with quorum). An n-way partial correspondence between elements of V1, V2,..., V
n
for a quorum q is defined as an n-way correspondence such that
such that , |cover(v)| ≥ q.
, |cover(v)| ≥ q.
We shall in the following use the notation .
.
As before, this restriction is computed by using the S relation. For instance a clique aggregation for a quorum q would be expressed as follows  and ∀i, j, (v
i
S v
j
) or (v
i
= *) or (v
j
= *).
and ∀i, j, (v
i
S v
j
) or (v
i
= *) or (v
j
= *).
Partial Network Alignment MultiGraph
The PNAM (Partial Network Alignment Multigraph) is an extension of the NAM (Network Alignment Multigraph) presented in [23]. It summarises both the n-way partial correspondence and the connectivity in the genomes (i.e. gene neighbourhood).
Definition (with quorum). A partial network alignment multigraph (PNAM) for n primary graphs G
i
= (V
i
, E
i
) is a graph such that:
such that:
-
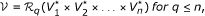
-

and
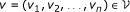 ,
, 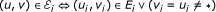
In other words, the vertices of the multigraph are n-tuples of genes and don't care elements and there is an edge e ∈ ℰ i (that is, an edge of colour i) between two vertices if they have genes at the ith position that are neighbours in the genome G i . In the following, we refer to such an edge as an edge of colour i.
Figure 2 gives an example of layered data graph for three genomes and the corresponding PNAM for a clique aggregator with q = 2.
Example of Partial Network Alignment Multigraph. A simple example of layered data graph (top) and partial network alignment multigraph PNAM (bottom). As in Figure 1, the S gene-to-gene relation is represented by dotted edges. Vertices of the PNAM (spines) correspond to cliques of the S relation. The difference with a NAM (Figure 1) is that "don't care" genes (represented as *) are now allowed in spines (here we have a quorum q = 2 which means we cannot have more than one * in a spine). The set of vertices of this PNAM can be partitioned into four syntons, three of them are singletons: {(a1, a2, a3)}, {(a1, *, a3)} and {(*, a2, a3)}, the fourth is of size 2: {(a1, a2, *), (b1, b2, *)}. Only two of them ({(a1, a2, a3)} and {(a1, a2, *), (b1, b2, *)}) are maximal.
Defining syntons in the PNAM
With the previous definition of a PNAM at hand, several definitions of synteny are possible, depending on the properties one is looking for (see Table 1).
For instance, without quorum (i.e. q = n) and if strict gene order has to be conserved, syntons are simply the connected components of the PNAM in which all edges that do not have all of the n colours are removed. Note that it is also possible to specify a partial gene order conservation, stating that, in a given synton, two spines consecutive for a colour should not be separated by more than δ shuffle spines for the other colours. This idea will not be developed in the present paper.
Since we want to allow all gene permutations, we shall use the most general definition, which is the following.
Definition (without quorum). A synton is a maximal subgraph of the PNAM such that ∀i ∈ [|1, n|],
of the PNAM such that ∀i ∈ [|1, n|],  is connected for
is connected for .
.
To introduce a quorum, one has to modify the previous definition in order to cope with the presence of don't care elements in the PNAM vertices.
Definition (with quorum). A synton is a maximal subgraph of the PNAM such that ∃I ⊆ [|1, n|], |I| ≥ q such that ∀i ∈ I,
of the PNAM such that ∃I ⊆ [|1, n|], |I| ≥ q such that ∀i ∈ I,  is connected for
is connected for and
and , cover(v) = I.
, cover(v) = I.
Informally, the first part of the definition ensures that the result will be a synton when restricted to the colours I, and the second part makes sure that for the colours i ∉ I, all the vertices of  correspond to a don't care element. In the previous definition, the term "maximal" naturally means that no other vertex of the PNAM can be added without breaking the connectivity conditions. With this definition, it is easy to show that syntons form a partition of the PNAM vertices.
correspond to a don't care element. In the previous definition, the term "maximal" naturally means that no other vertex of the PNAM can be added without breaking the connectivity conditions. With this definition, it is easy to show that syntons form a partition of the PNAM vertices.
The PNAM given in Figure 2 is thus partitioned into 4 syntons: {(a1, a2, a3)} (I = {1, 2, 3}), {(a1, *, a3)} (I = {1, 3}), {(*, a2, a3)} (I = {2, 3}) and {(a1, a2, *), (b1, b2, *)} (I = {1, 2}).
However, one can notice that although each class of this partition is maximal in the previous sense, it may not be maximal in terms of the genes involved. When projecting a synton onto the layered data graph, it may occur that the set of genes obtained is included into another projection (this occurs for instance when a synton on k genomes has the same boundaries as a synton on k + 1 genomes). It is therefore advisable to add another constraint to syntons in order to remove some redundancy in the results in terms of genes.
Definition of⊑. Let us denote by ⊑ the relation defined as follows: for u,  u ⊑ v ⇔ cover(u) ⊆ cover(v).
u ⊑ v ⇔ cover(u) ⊆ cover(v).
This means that all vertices in the spine u that are not "don't care" elements are also elements of the spine v.
This definition can be extended to subgraphs of the PNAM.
Definition of⊑. For two subgraphs of the PNAM C1 = (U1, F1,... F
n
) and , C1 ⊑ C2 ⇔ ∀u1 ∈ U1, ∃u2 ∈ U2, such that u1 ⊑ u2.
, C1 ⊑ C2 ⇔ ∀u1 ∈ U1, ∃u2 ∈ U2, such that u1 ⊑ u2.
We call then a maximal synton a synton that is maximal for the relation ⊑.
On the example of Figure 2, we have for instance {(a1, *, a3)} ⊑ {(a1, a2, a3)} which means {(a1, *, a3)} is not maximal. The only two maximal syntons in that example are {(a1, a2, a3)} and {(a1, a2, * ), (b1, b2, *)}.
Note that this constraint is not embedded into the algorithm but is added as a final filter on the results.
Algorithm
The most natural approach to compute syntons with quorum would be to build the PNAM, and then to use one of the graph partitioning algorithms at our disposal [17, 29].
However, we already showed in [23] that when the correspondence relation is not one-to-one, the size of the NAM may grow exponentially with the number of graphs. The situation for PNAM is even worse since for each vertex of the NAM we now have  additional vertices in the PNAM. This means that avoiding the explicit construction of the PNAM is an even bigger priority.
additional vertices in the PNAM. This means that avoiding the explicit construction of the PNAM is an even bigger priority.
In this paper, we choose to extend the graph partitioning algorithm described in [23]. The idea is to conduct a depth first search (DFS) of the classes starting with the connected components of the first colour (genome), and to add colours incrementally. Therefore the multigraph is not computed explicitly but instead smaller parts of it (classes) are computed on the fly in each branch of the DFS.
The basic algorithm is fully described in [23] and a summary pseudo-code is given below. The two main operations are:
-
SPLIT1...ithat splits a class on colours 1 to i;
-
EXPANDi+1that adds the (i + 1)thcolour to the current network alignment multigraph.
Algorithm 1: OTF.
Global: Layered Data Graph D = (V, E)
for the primary graphs G i = (V i , E i ), i ∈ [|1, n|]
Input: Multigraph C
/* current class: initialised with */
*/
Integer i/* current layer: initialised with 1 */
Variables: Partition P
/* current partition on the i first layers */
(1) begin /* partition on the i first layers */
(2) P ← SPLIT1...i(C),
(3) if (|P| ≠ 1) then /* C is split */
(4) for NewC ∈ P do
(5) OTF(NewC, i)
(6) end for
(7) else if (i < n) then /* C is stable */
(8) NC ← EXPANDi+1(C),
(9) OTF(NC, i + 1),
(10) else /* C is stable for all colours */
(11) PRINT(C)
(12) end if
(13) end
Initialisation
As in [23], the algorithm is initialised with all connected components on the first genome. In order to cope with missing genes on the first genome, one has only to add an initial singleton class containing a don't care vertex.
Expand
The procedure called EXPAND_V ERTICESi+1expands the current set C of PNAM vertices to two kinds of new (i + 1)-tuples.
The first case is similar to the no-quorum condition and expands each vertex v = {v1, v2,... v
i
} ∈ C by genes vi+1∈ Vi+1. These genes are called terminals of v. Ideally, a terminal vi+1is such that there exists an n-tuple  such that ∀j ∈ [|1, i + 1|], u
j
= v
j
(i.e. v is a prefix of u). In practice, the efficient computation of these terminals greatly depends upon the chosen aggregation function. For instance, for the clique, this is a simple task: (v1,..., vi+1) is required to be a clique too (don't care elements are ignored) since this is a necessary condition for the final n-tuple to be a clique. Using the ordering G 1, G 2, G 3 in the example given in Figure 2, this allows us to build the vertex (a 1, a 2, a 3) from the vertex (a 1, a 2).
such that ∀j ∈ [|1, i + 1|], u
j
= v
j
(i.e. v is a prefix of u). In practice, the efficient computation of these terminals greatly depends upon the chosen aggregation function. For instance, for the clique, this is a simple task: (v1,..., vi+1) is required to be a clique too (don't care elements are ignored) since this is a necessary condition for the final n-tuple to be a clique. Using the ordering G 1, G 2, G 3 in the example given in Figure 2, this allows us to build the vertex (a 1, a 2, a 3) from the vertex (a 1, a 2).
The second case is to extend v = (v1,... v i ) by a don't care element if this is allowed by the quorum condition, i.e. the total number of don't care elements is less than n -q. These added are intended to introduce the missing genes on genome i + 1. For instance, in Figure 2, with the same ordering G1, G2, G3, the vertex (c1, c2, *) is recovered thanks to the introduction of don't care elements as terminals (it is an expansion of the vertex (c1, c2)).
Split
As in [23], the SPLIT1-ioperation computes the connected components on each colour in turn. If, for a colour j, the class is split, then it returns the split parts.
The main difference is that the connected components for a colour j are now computed on P j (V), the restriction of the set of vertices to those that do not have a don't care element at position j.
This is simply done by:
-
1.
removing temporarily all tuples having a don't care element at position j,
-
2.
computing the connected components of the resulting set of vertices,
-
3.
adding back the previously removed set in each connected component.
Finally, just as in [23], when a class C is such that SPLIT1-i(C) = C then it is stable for colours 1 to i and needs expansion to the (i + 1) th colour.
Results and Discussion
In order to illustrate our approach in practice, we performed two different experiments. The first one is a comparison to a popular heuristics with a similar aim (I-ADHO RE). The second one is a study of the evolution rate of genes in synteny that generalises previous observations on this subject. In the remaining of this paper, we shall refer to our algorithm as OTFQ (OTF was the name of the algorithm in [23] and Q stands for quorum).
Comparison to I-ADHO RE
In this section, we compare the syntenies recovered by our approach to those found by I-ADHO RE[26], a popular program used to recover syntenies with missing genes.
ADHO RE and I-ADHO RE
ADHO RE[30] (Automatic Detection of Homologous Regions) looks for genomic regions between two genomes where the gene order is strictly conserved. The gene-to-gene (homology) relation S is, as in our approach, boolean and provided as input to the program together with the genes location. The algorithm basically proceeds by clustering of the homologous genes pairs based on the linear distance of the corresponding genes on both chromosomes (two pairs are close if they lie close together on the same diagonal of the alignment matrix) and a measure of the cluster linearity (how the set of pairs fits to a diagonal). The procedure allows for gaps (maximum number of intervening non-homologous genes between two pairs) but not explicitly for genes permutations although a limited amount of permutations is possible by considering them as gaps.
In 2004, the authors extended this method to the case of multiple genomes: the new version is called I-ADHO RE[26]. I-ADHO RE starts by collecting the results of ADHO RE obtained on each pair of genomes. The results are called "multiplicons of level 2". This series of multiplicons initialises a set ℳ that will eventually constitute the solution set.
The procedure starts with the largest (in terms of gene pairs) multiplicon and represents it as a "profile" i.e. a series of aligned positions without permutation. Next, this profile is aligned to the whole set of chromosomes using a variant of ADHO RE. One important point is that there is a match between a gene and a given position in the profile when this position contains at least one gene that matches. In other terms, in I-ADHO RE, spines are connected components of the S relation.
The results of this alignment are multiplicons of level 3 (they can be extensions of part or the totality of the original multiplicon). These new multiplicons are then put back in the ℳ set and the algorithm iterates. There is no need in I-ADHO RE for the quorum parameter we previously defined, instead the results are presented in the form of an arborescence of multiplicons (from level 2 to, possibly, level n) from which the spines involving at least q genomes can be easily retrieved.
Finally, this algorithm was improved in 2007: in this latest version - I-ADHO RE 2.0 [31] - a new alignment profile is recomputed for all segments of the current multiplicon after extension. This implies that some erroneous decisions taken at the beginning of the execution could be corrected later on.
Because I-ADHO RE is a heuristic (basically a greedy algorithm), its main advantage is that it is extremely quick. The main drawback is that the definition of a multiplicon is procedural rather than formal. This makes the comparison to other approaches more difficult since we do not know exactly what is to be found and what is missed. Because of this, in the following experiment we decided to compare the results in terms of genes involved in syntons (OTFQ) versus multiplicons (I-ADHO RE).
Data and parameters
In order to compare the two algorithms in various phylogenetic situations, we constituted four groups, each made of 5 or 10 bacterial species at variable phylogenetic distances (Table 2). The most heterogeneous group is the group bacteria, made of phylogenetically distant species. The most homogeneous is the group entero made of Enterobacteriaceae. The precise composition of each bacterial group is given in Table 2.
The gene-to-gene relation S is provided by BLASTP by selecting pairs of gene products with p - value ≤ 1e - 10, %identity ≥ 40 and with the alignment covering at least 80% of the smallest protein.
OTFQ was run with the following parameters: gaps of at most 3 genes (deltagap = 3), all gene permutations allowed (deltashuf = ∞), minimum synton size of 3 (mineltsize = 3) and a quorum q of at least 2 genomes. Spines are defined simply as connected components (CC) of S. Note that OTFQ allows other definitions of spines, as cliques or γ-quasi-cliques of S (for a spine made of n nodes, it means that for each node v we must have degree(v) ≥ γ* (n - 1)), those definitions are not used in this test.
For I-ADHO RE, we used the default parameters, except for "gap_size", "tandem_gap_size" et "cluster_gap" which were all set to 3 in order to be as consistent as possible with the deltagap parameter used in OTF. The "anchor_points" parameter, corresponding to the minimal number of genes in a cluster, was set to 3 in order to fit with the "mineltsize" parameter of OTF. Additionally, we set up the q value parameter very close to 0 and the prob cutoff parameter to 1, in order to disable any filtering and keep as many multiplicons as possible.
Notice that the chosen parameters are not optimal (both for I-ADHO RE and OTF) but were selected in order to make the comparison as consistent as possible. In particular, a quorum of 2 out of 10 genomes is usually too low for OTF since it potentially leads to an exponential growth of the solution size. However, we keep this value since I-ADHO RE naturally reports these multiplicons too.
Execution times
The execution times of I-ADHO RE and OTF for the different groups are given in Table 3.
We notice that for the more heterogeneous groups (bacteria, proteo, gamma), the OTFQ execution times are short, and indeed, shorter than for I-ADHO RE. Both are anyway shorter than the time needed to perform the initial all-against-all BLASTP comparisons needed to compute the S relation. However, this situation is inverted when working with close species and a larger number of genomes. For 10 enterobacteria, OTFQ runs out of memory (the limit was 2 Gb). Indeed a closer examination of running times shows that I-ADHO RE behaves roughly quadratically with the number of genomes (as expected if the computation time is dominated by the initial pairwise comparison and not by the following greedy search) whereas the OTFQ runtime grows exponentially with this number. However, Table 3 shows that for up to 10 genomes, the problem remains amenable to an exact algorithm and there is therefore no need to resort to heuristics. We should observe however that I-ADHO RE was specifically designed to deal with large eukaryotic genomes, whereas our definitions and algorithm are better suited to the alignment of bacterial genomes (one of the differences, for instance, is that we do not look for intra-genomic syntenies).
Comparison of results
As mentioned before, in order to compare more easily the results of I-ADHO RE (multiplicons) and OTFQ (syntons), we choose to project them back onto the layered data graph (i.e. genomes) and, therefore, to compare sets of genes involved in multiplicons versus syntons. In this comparison, "gap" genes (i.e. genes not involved in any spine for OTFQ and non "anchor" genes for I-ADHO RE) are ignored. This is shown in Table 3. We first observe that the number of genes found in multiplicons and syntons are very close, they range from 3% of the total number of genes for distant species (bacteria group), and to up to 66% for very close species (entero group). Moreover, OTFQ constantly finds slightly more genes than I-ADHO RE (from 10 to 20% irrespective of the phylogenetic group) and, except for the 10-bacteria group where the overlap is 91%, the set of genes found in multiplicons are almost totally included in the sets found in syntons (from 99 to 100%). A closer examination of these results shows that missed genes come from three main reasons, all of them being related to the linearity and collinearity constraint in I-ADHO RE. The first, and more important, reason comes from the definition of "gap" genes. In OTFQ "gaps" are simply genes that do not belong to a spine within the considered synton (they may have no homologous genes or they may be involved in a spine from another synton). In I-ADHO RE the definition is similar but multiplicons have an additional linearity constraint that may be broken when the number of "gaps" on one genome is not counterbalanced by an equivalent number of "gaps" on the other one. With 3 "gaps" for instance, a synteny can be missed when two genes are adjacent on one chromosome and their homologous genes are separated by more than 2 gaps on the other chromosome. This linearity condition makes the interpretation of the "gaps" parameter more delicate. Unfortunately, we did not find any I-ADHO RE parameter to change this behaviour but we believe this could be fixed easily. The second reason is due to the existence of gene order permutations and is therefore more fundamentally related to the I-ADHO RE algorithm, that enforces strict collinearity of genes. Finally, a third case marginally arises from an inversion of the orientation of one gene. This comes from the fact that I-ADHO RE considers gene orientation in its definition whereas OTFQ ignores it.
Figure 3 is an illustration of gene order permutation in the case of the glycogen metabolism. Glycogen is the major reserve of polysaccharide in bacteria, its biosynthesis from glucose-1-phosphate is performed in three steps by GlgC (ADP-glucose pyrophosphorylase), GlgA (glycogen synthase) and GlgB (branching enzyme) in that order [32]. Two additional enzymes, GlgX (glycogen debranching enzyme) and GlgP (gycogen phosphorylase), are involved in the reverse process, i.e. in glycogen degradation. All of the corresponding genes are often found clustered together in single or adjacent operons [32, 33] but in various orders. The most frequent order for the glgA/B/C triplet is BCA (e.g. in E. coli on Figure 3) but the order CBA is also observed (e.g. in M. capsulatus in Figure 3, that also displays an inversion of glgC. Finally the order BAC, although rare, is observed too (in Clostridium perfringens for instance (data not shown)). The genes glgP and glgX are not always present close to the glgA/B/C triplet but, when they are, their order is very variable. For instance, glpP lies before glgB in F. nucleatum and R. sphaeroides but after glgA in B. subtilis and E. coli. The same situation holds for glgX in E. coli and R. sphaeroides (Figure 3). Finally, it is important to notice that the GlgA sequence is not well conserved across bacterial species but is actually split in two groups [32], one is characteristic of Bacilli, Fusobacteria and Clostridia, the second one is characteristic of Alpha and Gamma proteobacteria. This is the reason why, at a reasonable BLASTP threshold, the GlgA group (red lines in Figure 3) does not form a single connected component but two disjoint components. When these five species are subjected to analysis by the two programs, they give rise to different multiplicons/syntons, reflecting the different ways permutations are handled. I-ADHO RE gives rise to 3 multiplicons of level 2 (i.e. involving only pairs of genomes). Each of them is composed of 3 genes: F. nucleatum/E. coli {B, C, P }, F. nucleatum/B. subtilis {A, C, B} and E.coli/R. sphaeroides {A, C, B}. Let us notice that the E.coli/B. subtilis {B, C, P } is missed because the two gaps in B. subtilis break the multiplicon collinearity condition. By contrast, OTFQ finds 4 syntons of larger size. The E.coli/R. sphaeroides synton now involves all of the 5 genes: {A, B, C, P, X}. Similarly the F. nucleatum/B. subtilis now involves 4 genes {A, B, C, P }. The E.coli/R. sphaeroides synton includes M. capsulatus as well: {A, B, C}. And finally, OTFQ also finds a synton, {B, C, P }, with 4 species: F. nucleatum/B. subtilis/E. coli/R. sphaeroides. Notice that, because of the broken connection on glgA, no multiplicon nor synton of size at least 3 genes can be found on all of the five species depicted here.
Another example of conserved gene neighbourhood with gene permutation is provided by the biotin (vitamin H) biosynthetic pathway. Although biotin is an essential enzyme cofactor in all forms of life, its detailed biosynthetic pathway is not yet fully understood [34]. Indeed, the well documented part of the pathway comprises the four late steps, leading to biotin from pimeloyl-CoA and catalyzed by BioF, BioA, BioD and BioB [35]. In bacteria, the four corresponding genes usually form an operon (or regulon) cluster [35]. This cluster sometimes includes additional bio genes involved in the earlier steps leading to pimeloyl-CoA. For instance BioW synthesizes pimeloyl-CoA from pimelic acid and BioC and BioH have recently been suggested to participate in the synthesis of pimeloyl-CoA from malonyl-CoA [34]. Figure 4 displays the gene layout of the bioF/A/D/B core cluster in five bacterial species. As shown, each species displays a specific gene order: BFDA (A. tumefaciens), AFDB (B. licheniformis), ADFB (B. thuringiensis), ABFD (E. coli) and DABF (S. aureus). Because of this high level of gene shuffling, i - ADHoRe was only able to retrieve a single multiplicon involving two species (A. tumefaciens - E. coli) and three genes (bioB/F/D). The bioA/B/F cluster between E. coli and S. aureus was missed because of the opposite gene orientation of bioA. By contrast, OTFQ could retrieve three different syntons, of much larger sizes. The first synton involves the four bioF/A/D/B genes in all species but S. aureus. This comes from the fact that bioD is not well conserved in S. aureus and was therefore not connected to any other bioD gene at the selected BLASTP threshold. The second synton is therefore composed of the three bioF/A/B genes, in all of the five species. Finally, the third synton is composed of the four bioW/A/F/B genes in B. licheniformis and S. aureus. Again, bioD is missing from this latter synton because of a lack of sequence similarity. The same is true for bioC between B. thuringiensis and E. coli.
Synteny and gene evolutionary rates
As mentioned in the introduction, bacterial syntenies can provide useful information about evolutionary processes. For instance, Lemoine et al. have shown [36] that genes in synteny groups are subjected to stronger evolutionary pressure than genes outside of synteny groups. They started by identifying pairs of orthologous genes between two bacterial genomes. A given pair is then classified as a POG (Positional Ortholog Group) if it is strictly adjacent to (at least) another pair of orthologous genes. Finally, the PAM distances (as computed with the DARWIN package [37]) between the elements of a pair are computed for the POG and non-POG groups and their distribution are compared.
Using this approach on several pairs of bacterial species, from closely related enterobacteria (E. coli and S. enterica) to more distant species (E. coli and B. subtilis), they showed that the mean d PAM in POG s is significantly lower than the mean d PAM in non-POG, thus indicating that genes within synteny groups are generally more conserved than genes outside of synteny groups.
In this section, we attempt to generalise this result in two ways: first by working with more than two genomes, and second by investigating if the same evolutionary trends is observed as a function of the size of the synteny group.
To this purpose, we use the same four sets of five species (bacteria, proteo, gamma and entero) as defined before. In the context of an evolutionary study, we need to modify our previous definition of the gene-to-gene correspondence since we want to enforce a true orthology relationship and not simply a sequence similarity relationship. To this purpose, we make use of the IN PARANOID program [27]. Two genes from different genomes are related by S if they belong to the same group of co-orthologs provided by IN PARANOID. Moreover, in order to enforce a more stringent definition of synteny, we use a gap parameter of 0, a quorum of 3 genomes and we force spines to be cliques of the S relation. This means that a spine is composed of at least three genes that should be all pairwise related by S. We then run OTFQ on the four sets separately (with a minimum synton size of 1, in order to recover isolated spines as well) and we further process the result in the following way. For a given pair of S related genes, we record the size of the largest synton to which it belongs (let us denote it by max
size
), we compute its PAM distance using the same procedure as in [36] (denoted by d
PAM
) and we then analyse the distribution of d
PAM
within each group of max
size
. The results are presented, for each of the four species group, in Figure 5 where the black curve displays the median of d
PAM
as a function of the synteny size (max
size
). In order to get sufficient statistics (we requested a minimum of 500 pairs in each bin), values of max
size
greater than a certain limit are pooled within the same bin (indicated by the "+" postfix in the figure). A first point to observe is the value of the median for max
size
= 1 (i.e. for pairs of orthologs only present in isolated spines) versus the values for max
size
> 1. The median values (this is true also for the mean) are always higher for these isolated orthologs than for orthologs involved in larger blocks of synteny. This confirms the results already obtained by Lemoine et al. To be exhaustive, one should note that there is a (quantitatively smaller) category of pairs that are not displayed on this plot: namely orthologs that are not involved in any clique-spine of at least 3 genomes. For all of the 4 groups, their d
PAM
median values are always higher than for the first group. We choose not to plot them because the co-orthology relationship may be considered as dubious in these cases. The second point to observe is that there is a clear tendency for d
PAM
to decrease when the synteny size increases. This effect is more pronounced for distant species (bacteria, proteo and gamma) than for closely related species (entero). In order to make sure that this effect is not related to some phylogenetic heterogeneity in the data sets, we also split the analysis by pairs of species. This is represented by the  coloured curves in Figure 5 This clearly shows that the same trend holds whatever the pair of species considered (although some species pairs have globally lower or higher values). In order to remove a possible bias arising from false positive orthologs in IN PARANOID, we additionally performed the same analysis restricted to one-to-one orthologs (i.e. ignoring all groups of co-orthologs of size greater than 2 genes). The curves are then slightly shifted towards lower values of d
PAM
but keep the same shape as presented here. As a conclusion we can extend the results presented by Lemoine et al. in the following way: for a given pair of orthologous genes, the larger the size of the synteny in which it is involved, the more conserved the pair is.
coloured curves in Figure 5 This clearly shows that the same trend holds whatever the pair of species considered (although some species pairs have globally lower or higher values). In order to remove a possible bias arising from false positive orthologs in IN PARANOID, we additionally performed the same analysis restricted to one-to-one orthologs (i.e. ignoring all groups of co-orthologs of size greater than 2 genes). The curves are then slightly shifted towards lower values of d
PAM
but keep the same shape as presented here. As a conclusion we can extend the results presented by Lemoine et al. in the following way: for a given pair of orthologous genes, the larger the size of the synteny in which it is involved, the more conserved the pair is.
Distribution of d PAM . Distribution of d PAM within each group of max size (size of the maximal synton in which a given pair of orthologs appears). The black curve corresponds to the median of d PAM on the whole set, whereas the coloured curves correspond to the analysis split by pairs of species. We observe in all cases a clear tendency for d PAM to decrease when the synteny size increases.
Conclusions
In this paper, we presented an extension of the graph alignment algorithm proposed in [23] based on a clear-cut definition of bacterial syntenies, as well as an exact algorithm to find them. The main purpose of this new extension is to allow for missing genes. More precisely, we now require genes to be present only on a quorum q ≤ n of the genomes under study. Together with a very flexible definition of block of synteny (n-way genes aggregation in spines, presence of gap genes, partial or total conservation of the gene order), this resulted in a versatile tool to study syntenies in bacteria, that may be adapted to various kinds of studies. We presented two typical applications. The first one is related to the search of functional gene associations (for instance to the purpose of genome annotation). In this context, one should choose a quite loose gene-to-gene relationship based on sequence similarity and relaxed synteny parameters. We compared our approach to the widely used heuristics I-ADHO RE. Execution times and results are very similar, showing that, at least up to ten genomes, the problem is still tractable with an exact definition and algorithm. The second application is related to evolutionary studies. In this context, it is better to work with a tighter definition of syntenies (orthology relation, clique association of genes, absence of gaps). We showed that the syntons retrieved by the algorithm presented an already documented feature: isolated pairs of orthologs are less conserved than the ones involved in larger blocks of synteny. However, we could extend this observation in two ways: first by working with multiple comparisons (i.e. by focusing on syntenies occurring on at least 3 genomes) and, second, by showing that the larger the block is, the more conserved the genes are.
Finally, we would like to stress that, although this paper and its illustrations focus on the question of syntenies, the definitions and the algorithm presented herein are applicable as well to the more general context of graphs alignments. For biological data, other possible applications could therefore concern the alignment of metabolic graphs, of PPI graphs or even of mixed data (e.g. metabolic versus genomic data [17]).
Availability
The algorithm has been implemented in Java, is platform independent and is distributed as open-source (GPL). Source code, user's documentation and samples files are available for download at: http://www.inrialpes.fr/helix/people/viari/lxgraph
References
NCBI: Complete Microbial Genomes[http://www.ncbi.nlm.nih.gov/genomes/lproks.cgi]
Huynen M, Bork P: Measuring genome evolution. Proc Natl Acad Sci USA 1998, 95: 5849–5856. 10.1073/pnas.95.11.5849
Koonin E, Wolf Y: Genomics of bacteria and archaea: the emerging dynamic view of the prokaryotic world. Nucl Acids Res 2008, 36: 6688–6719. 10.1093/nar/gkn668
Itoh T, Takemoto K, Mori H, Gojobori T: Evolutionary Instability of Operon Structures Disclosed by Sequence Comparisons of Complete Microbial Genomes. Mol Biol Evol 1999, 16: 332–346.
Dandekar T, Snel B, Huynen M, P B: Conservation of gene order: A fingerprint of proteins that physically interact. Trends Biochem Sci 1998, 23: 324–328. 10.1016/S0968-0004(98)01274-2
Tesler G: GRIMM: genome rearrangements web server. Bioinformatics 2002, 18(3):492–493. 10.1093/bioinformatics/18.3.492
Sinha A, Meller J: Cinteny: flexible analysis and visualization of synteny and genome rearrangements in multiple organisms. BMC Bioinformatics 2007, 8: 82. 10.1186/1471-2105-8-82
Uno T, Yagiura M: Fast Algorithms to Enumerate All Common Intervals of Two Permutations. Algorithmica 2000., 26:
Heber S, Stoye J: Algorithms for Finding Gene Clusters. WABI: International Workshop on Algorithms in Bioinformatics, LNCS 2001.
Didier G: Common intervals of two sequences. Algorithms in Bioinformatics Proceedings, Volume 2812 of Lecture Notes in Bioinformatics 2003, 17–24.
Bergeron A, Corteel S, Raffinot M: The Algorithmic of Gene Teams. WABI: International Workshop on Algorithms in Bioinformatics, Volume 2452 of Lecture Notes in Computer Science 2002, 464–476.
He X, Goldwasser M: Identifying Conserved Gene Clusters in the Presence of Homology Families. J Comput Biol 2005, 12(6):638–656. 10.1089/cmb.2005.12.638
Pasek S, Bergeron A, Risler J, Louis A, Ollivier E, Raffinot M: Identification of genomic features using microsyntenies of domains: Domain teams. Genome Res 2005, 15(6):867–874. 10.1101/gr.3638405
Kim S, Choi JH, Yang J: Gene Teams with Relaxed Proximity Constraint. IEEE Computational Systems Bioinformatics Conference (CSB 2005) 2005, 44–55.
Ling X, He X, Xin D, Han J: Efficiently Identifying Max-Gap Clusters in Pairwise Genome Comparison. J Comput Biol 2008, 15(6):593–609. 10.1089/cmb.2008.0010
Ling X, He X, Xin D: Detecting gene clusters under evolutionary constraint in a large number of genomes. Bioinformatics 2009, 25(5):571–577. 10.1093/bioinformatics/btp027
Boyer F, Morgat A, Labarre L, Pothier J, Viari A: Syntons, metabolons and interactons: an exact graph-theoretical approach for exploring neighbourhood between genomic and functional data. Bioinformatics 2005, 21(23):4209–4215. 10.1093/bioinformatics/bti711
Calabrese P, Chakravarty S, Vision T: Fast identification and statistical evaluation of segmental homologies in comparative maps. ISMB (Supplement of Bioinformatics), Volume 19 2003, 74–80.
Haas B, Delcher A, Wortman J, Salzberg S: DAGchainer: a tool for mining segmental genome duplications and synteny. Bioinformatics 2004, 20(18):3643–3646. 10.1093/bioinformatics/bth397
Wang X, Shi X, Li Z, Zhu Q, Kong L, Tang W, Ge S, Luo J: Statistical inference of chromosomal homology based on gene colinearity and applications to Arabidopsis and rice. BMC Bioinformatics 2006, 7: 447. 10.1186/1471-2105-7-447
Rödelsperger C, Dieterich C: Syntenator: multiple gene order alignments with a gene-specific scoring function. Algorithms for Molecular Biology 2008, 3: 14. 10.1186/1748-7188-3-14
Rödelsperger C, Dieterich C: CYNTENATOR: progressive gene order alignment of 17 vertebrate genomes. PloS one 2010, 5: e8861. 10.1371/journal.pone.0008861
Denielou YP, Boyer F, Viari A, Sagot MF: Multiple Alignment of Biological Networks: A Flexible Approach. CPM: 20th Symposium on Combinatorial Pattern Matching, Volume 5577 of Lecture Notes in Computer Science 2009, 263–273.
Ogata H, Fujibuchi W, Goto S, Kanehisa M: A heuristic graph comparison algorithm and its application to detect functionally related enzyme clusters. Nucl Acids Res 2000, 28(20):4021–4028. 10.1093/nar/28.20.4021
Kalaev M, Bafna V, Sharan R: Fast and Accurate Alignment of Multiple Protein Networks. International Conference on Research in Computational Molecular Biology RECOMB 2008, Volume 4955 of Lecture Notes in Computer Science 2008, 246–256.
Simillion C, Vandepoele K, Saeys Y, Van de Peer Y: Building genomic profiles for uncovering segmental homology in the twilight zone. Genome Res 2004, 14(6):1095–1106. 10.1101/gr.2179004
Remm M, Storm C, Sonnhammer E: Automatic clustering of orthologs and in-paralogs from pairwise species comparisons. J Mol Biol 2001, 314: 1041–1052. 10.1006/jmbi.2000.5197
Altenhoff A, Dessimoz C: Phylogenetic and Functional Assessment of Orthologs Inference Projects and Methods. PloS Comput Biol 2009, 5: e1000262+.
Habib M, Paul C, Raffinot M: Maximal Common Connected Sets of Interval Graphs. CPM: 15th Symposium on Combinatorial Pattern Matching, Volume 3109 of Lecture Notes in Computer Science 2004, 347–358.
Vandepoele K, Saeys Y, Simillion C, Raes J, Van De Peer Y: The automatic detection of homologous regions (ADHoRe) and its application to microcolinearity between Arabidopsis and rice. Genome Res 2002, 12(11):1792–1801. 10.1101/gr.400202
Simillion C, Janssens K, Sterck L, Van de Peer Y: i-ADHoRe 2.0: an improved tool to detect degenerated genomic homology using genomic profiles. Bioinformatics 2008, 24: 127–128. 10.1093/bioinformatics/btm449
Cho K, Lim W, Math R, Asraful Islam S, Hong S, Kim H, Yun H: Comparative analysis of the glg operons of Pectobacterium chrysanthemi PY35 and other prokaryotes. J Mol Evol 2008, 67: 1–12. 10.1007/s00239-008-9103-7
Montero M, Almagro G, Eydallin G, Viale A, Muñoz F, Bahaji A, Li J, Rahimpour M, Baroja-Fernàndez E, Pozueta-Romero J: Escherichia coli glycogen genes are organized in a single glgBXCAP transcriptional unit possessing an alternative suboperonic promoter within glgC that directs glgAP expression. Biochem J 2010, 433: 107–117.
Lin S, Hanson R, Cronan J: Biotin synthesis begins by hijacking the fatty acid synthetic pathway. Nat Chem Biol 2010, 6(9):682–688. 10.1038/nchembio.420
Rodionov D, Mironov A, Gelfand M: Conservation of the biotin regulon and the BirA regulatory signal in Eubacteria and Archaea. Genome Res 2002, 12(10):1507–1516. 10.1101/gr.314502
Lemoine F, Lespinet O, Labedan B: Assessing the evolutionary rate of positional orthologous genes in prokaryotes using synteny data. BMC Evol Biol 2007, 7: 237. 10.1186/1471-2148-7-237
Gonnet G, Hallett M, Korostensky C, Bernardin L: Darwin v. 2:0: an interpreted computer language for the biosciences. Bioinformatics 2000, 16: 101–103. 10.1093/bioinformatics/16.2.101
Acknowledgements and Funding
We would like to thank Anne Morgat from the Swiss Institute of Bioinformatics for helpful discussions about the glycogen and biotin operons. YPD, AV and MFS are supported by INRIA. FB is supported by INRA. This work was funded by the French project ANR MIRI BLAN08-1335497 and the ERC Advanced Grant SISYPHE.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Authors' contributions
Devised the algorithm: YPD AV FB MFS. Implemented the algorithm and performed the analysis: YPD AV. Wrote the paper: YPD AV MFS. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Deniélou, YP., Sagot, MF., Boyer, F. et al. Bacterial syntenies: an exact approach with gene quorum. BMC Bioinformatics 12, 193 (2011). https://doi.org/10.1186/1471-2105-12-193
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2105-12-193



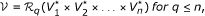

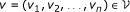 ,
,