- Research
- Open access
- Published:
The choice of null distributions for detecting gene-gene interactions in genome-wide association studies
BMC Bioinformatics volume 12, Article number: S26 (2011)
Abstract
Background
In genome-wide association studies (GWAS), the number of single-nucleotide polymorphisms (SNPs) typically ranges between 500,000 and 1,000,000. Accordingly, detecting gene-gene interactions in GWAS is computationally challenging because it involves hundreds of billions of SNP pairs. Stage-wise strategies are often used to overcome the computational difficulty. In the first stage, fast screening methods (e.g. Tuning ReliefF) are applied to reduce the whole SNP set to a small subset. In the second stage, sophisticated modeling methods (e.g., multifactor-dimensionality reduction (MDR)) are applied to the subset of SNPs to identify interesting interaction models and the corresponding interaction patterns. In the third stage, the significance of the identified interaction patterns is evaluated by hypothesis testing.
Results
In this paper, we show that this stage-wise strategy could be problematic in controlling the false positive rate if the null distribution is not appropriately chosen. This is because screening and modeling may change the null distribution used in hypothesis testing. In our simulation study, we use some popular screening methods and the popular modeling method MDR as examples to show the effect of the inappropriate choice of null distributions. To choose appropriate null distributions, we suggest to use the permutation test or testing on the independent data set. We demonstrate their performance using synthetic data and a real genome wide data set from an Aged-related Macular Degeneration (AMD) study.
Conclusions
The permutation test or testing on the independent data set can help choosing appropriate null distributions in hypothesis testing, which provides more reliable results in practice.
Background
Single-nucleotide polymorphisms (SNPs) serve as markers for mapping disease-associated genetic variants. It has been well known that SNP profiles are associated with a variety of diseases [1]. High-throughput genotyping technologies have been used to assay hundreds of thousands of SNPs in the human genome. Many single-locus based methods [2] have been proposed and many susceptibility determinants have been identified [1]. However, these identified SNPs seem to be insufficient in explaining the genetic contributions to complex diseases [3]. Researchers start to suspect that the causality of many common disease are more related with gene-gene interactions rather than with single genetic variations [3, 4]. For many common complex diseases, some SNPs have shown little main effects while their interactions are significantly associated with disease traits [5–7]. Consequently, detecting gene-gene interactions is a topic of current interest in GWAS [4]. Many methods have recently been proposed to identify interaction patterns associated with diseases, including MDR [6], CPM [5], RPM [8], BGTA [9], SNPRuler [10], LASSO [11–13], HapForest [14], BOOST [15], PLINK [16], BEAM [17], SNPHarvester [18] and INTERSNP [19]. However, a key issue of applying most of these methods in GWAS is the computational burden [4]. For example, to find pairwise interactions from 500,000 SNPs, we need 1.25 × 1011 statistical tests in total. To address this issue, screening approaches [20] have been proposed. The whole process of detecting gene-gene interactions is then divided into three stages:
-
Screening: Evaluate the importance of each SNP and assign it a score. Those SNPs with scores lower than the given threshold are removed without further consideration. Often a small portion of SNPs remains. This stage is often accomplished by fast algorithms using heuristics to reduce the search space of the next stage. One example is the popular screening method Tuning ReliefF [21].
-
Modeling: Search for the best combination of SNPs in the remaining SNPs. The exhaustive search can be used in this stage because the number of remaining SNPs is small, e.g., the popular modeling methods MDR and CPM. During the search process, the importance of a SNP combination is often measured by its prediction accuracy (typically evaluated by cross-validation). Thus, the best SNP combination and its corresponding interaction pattern can be identified in term of prediction accuracy.
-
Testing: Assess the significance of interaction patterns by hypothesis testing.
Hypothesis testing employed in the testing stage is also referred to as “feature assessment” in [22]. A critical issue in feature assessment is to choose an appropriate null distribution for hypothesis testing. An inappropriate null distribution may lead to an over-optimistic result (high false positive error) or an over-conservative result (high false negative error) [23]. Figure 1 gives a toy example. In this figure, null distribution 1 follows the χ2 distribution with the degree of freedom df = 4, denoted as  , and null distribution 2 follows
, and null distribution 2 follows  . If the true null distribution is
. If the true null distribution is  , then using
, then using  for hypothesis testing will give many false positive results.
for hypothesis testing will give many false positive results.
A toy example illustrating the effect of the inappropriate choice of null distributions. Null distribution 1 follows the  and null distribution 2 follows the
and null distribution 2 follows the  . The observed χ2 value is 10, and the P-values are 0.0404 and 0.2650 for these two null distributions, respectively. Suppose P = 0.05 is the threshold of hypothesis testing. Then P = 0.0404 indicates a significant result, while P = 0.2650 does not. If the true null distribution is
. The observed χ2 value is 10, and the P-values are 0.0404 and 0.2650 for these two null distributions, respectively. Suppose P = 0.05 is the threshold of hypothesis testing. Then P = 0.0404 indicates a significant result, while P = 0.2650 does not. If the true null distribution is  , then the use of
, then the use of  will give many false positive results.
will give many false positive results.
In this paper, we show through simulations that both screening and modeling may change the null distribution used in hypothesis testing. However, many methods (such as MDR combined with Tuning ReliefF [6, 21] and some other stage-wise methods [24]) neglect the rightward shift of the original null distribution (as illustrated in Figure 1) caused by screening and modeling. They inevitably suffer from the higher false positive rate. We have also noticed that some methods [25–27] modify the test statistics, which causes the leftward shift of the original null distribution. If we still stick to the theoretical null distribution in hypothesis testing, we may produce conservative results (see the discussion section). To address this issue, we suggest to use the permutation test and testing on the independent data set. The permutation test uses the re-sampling method to estimate the changed null distribution for hypothesis testing. Testing on the independent data set can reserve the theoretical null distribution. Through simulation experiments and the experiment on a real genome-wide data set from an AMD study, we demonstrate that the appropriate choice of null distributions leads to more reliable results.
Results
Simulation study of the inappropriate choice of null distributions
The huge number of SNPs in GWAS poses a heavy computational burden for detecting gene-gene interactions. The exhaustive search of all pairwise interactions and further using cross-validation to evaluate them (e.g. MDR [6]) become impractical in GWAS. To make it computationally feasible, a screening method is applied to the whole data set to pre-select a small subset of SNPs. Then the exhaustive search can be applied to identify the most likely disease-associated SNPs. At last, hypothesis testing is conducted on identified SNPs. The importance of hypothesis testing is briefly discussed in the discussion section. Here we use MDR and some efficient screening methods [21, 28–30] as examples to show that null distributions are affected by these methods Throughout this paper, we use the latest MDR software (MDR 2.0 beta 8.1) to perform all experiments. It also implements various screening methods, such as ReliefF, Tuning ReliefF, and SURFSTAR. We first show that the modeling process of MDR changes the null distribution in its search process. Then we show that MDR coupled with some screening methods further changes the null distribution.
The null distribution of MDR
MDR is a popular non-parametric approach for detecting all possible k-way (k = 2,…, d) combinations of SNPs that interact to influence disease traits. MDR runs 10-fold cross-validations, and uses the prediction errors and the consistencies to search for the optimal set of k-way interactions. For each of the selected k-way interactions, MDR constructs a 2 × 2 contingency table by partitioning the samples into the high-risk and low-risk groups. Then MDR conducts hypothesis testing based on this 2 × 2 contingency table. Table 1 illustrates how this is done by MDR. The authors claimed that MDR could reduce the k dimensional model into a 1 dimensional model [6]. Therefore, the current MDR software conducts the statistical test on a 2 × 2 contingency table using 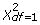 as its null distribution. This statement is biased because the higher dimensional space has to be browsed in order to construct the 2 × 2 continency table [31]. Here we use simulation experiments to show the correct null distribution in hypothesis testing for MDR.
as its null distribution. This statement is biased because the higher dimensional space has to be browsed in order to construct the 2 × 2 continency table [31]. Here we use simulation experiments to show the correct null distribution in hypothesis testing for MDR.
We design two scenarios with three settings of d-way interactions (d = 2, 3, 4), one showing the true null distributions of MDR (without search) and another showing the change of null distributions of MDR (with search). For each scenario of this experiment, we generate 500 null data sets, each of which contains 2,000 samples.
In the first scenario, we generate data sets containing two, three and four SNPs for the settings d = 2, 3, 4, respectively. All SNPs are generated using the Hardy-Weinberg principle with minor allele frequencies uniformly distributed in [0.05,0.5]. By doing so, the MDR model can be directly fitted without search. Let us take d = 2 as an example. For each null data set, we first obtain a genotype contingency table as shown in Table 1, and then collapse it into a 2 × 2 contingency table. Next we conduct the statistical test (either the Pearson χ2 test or the likelihood ratio test can be used since their difference is ignorable). The histogram of the statistics forms the null distribution. For d = 3,4, this can be done in the same way. The histograms of these null distributions obtained from 500 null data sets are shown in the upper panel of Figure 2. We observe that the null distributions of MDR (without search) follow the χ2 distributions. The estimated degrees of freedom of the χ2 distributions are df = 4.84, df = 11.40 and df = 30.41 for d = 2, d = 3 and d = 4, respectively. The non-interger degree of freedom is well defined, see [31–33]. This clearly indicates that 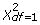 is not an appropriate null distribution for MDR.
is not an appropriate null distribution for MDR.
Null distributions affected by MDR modeling. The null distributions are estimated using 500 simulated null data sets. Each null data set contains n = 2000 samples. Upper panel: From left to right, each data set has L = 2, L = 3, L = 4 SNPs. MDR can be applied to these data sets without model search to fit the two-factor model (d = 2), the three-factor model (d = 3), and the four-factor model (d = 4). The resulting null distributions follows χ2 distributions with df = 4.84, 11.40, 30.41, respectively. Lower panel: Each null data set contains n = 2000 samples and L = 20 SNPs. MDR is directly applied to each data set. MDR searches all possible models and cross-validation is used to assess each model. The best two-factor model (d* = 2), the best three-factor model (d* = 3), and the best four-factor model (d* = 4) are identified. Their distributions, shown from left to right, do not strictly follow χ2 distributions.
In the second scenario, we generate the data sets containing 20 SNPs for all three cases. These SNPs are generated in the same way as in the first scenario. In this scenario, MDR first searches for the best d*-way interactions using 10-fold cross-validation and then conducts the testing. The results are shown in the lower panel of Figure 2. Compared with the first scenario, the null distributions change when MDR searches for the best d*-way interactions (d* = 2, 3,4) in d = 20 dimensions. We see that the null distributions do not strictly follow χ2 distributions. We use χ2 distributions to approximate them, and obtain their degrees of freedom as df = 13.76, df = 29.49 and df = 64.64, respectively.
In summary, our result shows the following facts:
-
The null distribution in MDR does not follow
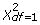 even when search process is not involved.
even when search process is not involved. -
The null distribution in MDR further changes when the search process is involved.
Therefore, hypothesis testing using 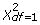 as the null distribution in MDR will give many false positive results.
as the null distribution in MDR will give many false positive results.
The null distribution for MDR combined with screening methods
MDR works well for small studies with 100 or less SNPs. In GWAS, it is not practical to use this exhaustive search method. Therefore, many screening methods have been proposed to reduce the number of SNPs before MDR is applied to detect d*-way interactions. These screening methods include ReliefF [28, 29], Tuning ReliefF (TURF) [21], SURF [34], SURFSTAR [30]. The reader is referred to [20] for a recent review on these screening methods.
The issue here is that after these screening methods are applied, the null distributions are further changed. To show the effect of screening methods on the null distribution, we generate 500 null data sets. Each data set contains 2,000 samples and each sample contains L = 2,000 SNPs. All SNPs are generated using the Hardy-Weinberg principle with minor allele frequencies uniformly distributed in [0.05,0.5]. Different screening methods, such as ReliefF, TURF, SURFSTAR, are first applied to reduce L = 2,000 SNPs to d = 20 SNPs. After that, MDR is applied to find the best d*-way interactions (d* = 2, 3, 4). Figure 3 presents the experiment results. The lower panel of Figure 2 serves as the reference distributions. It is obvious that all three screening methods further change the null distributions.
Null distributions affected by screening methods. The null distributions are estimated using 500 simulated null data sets. The null distributions shown in the lower panel of Figure 2, serve as the reference distributions (df = 13.76 for d* = 2, df = 29.49 for d* = 3 and df = 64.64 for d* = 4). The screening methods ReliefF, TURF and SURFSTAR are used to reduce the number of SNPs from L = 2000 to d = 20. For the remaining d = 20 SNPs, MDR is used to identify the best d*-way interactions (d* = 2, 3, 4). The resulting null distributions of these models, shown from left to right, do not strictly follow the χ2 distribution. The null distributions shift rightwards, compared with those distributions in the lower panel of Figure 2.
Simulation study of the suggested solutions
Two solutions are suggested in the method section. The first one is the permutation test and the second is testing on the independent data set. The permutation test works well to estimate null distributions in practice. Although the computational cost of this method is high, it is still feasible to be applied in GWAS when an efficient screening method is available. It is unnecessary to show its performance in simulation studies since it is a standard way of calibrating the null distribution in hypothesis testing [35, 36]. We demonstrate its performance using a real genome-wide data set from an AMD study in the next section. Here we show that the null distribution does not change when testing on an independent data set. We generate 500 null data sets. Each data set contains 2,000 samples and each sample has L = 2,000 SNPs. Each data set is partitioned into three subsets as nearly equal as possible: D(1), D(2), D(3). The screening method ReliefF is first applied to D(1), and the number of SNPs is reduced from L = 2,000 to d = 20 SNPs. The indices of the remaining 20 SNPs are collected in A1. After that, stepwise logistic regression (LR) is applied to D(2) to find the best d*-way interactions (d* = 2, 3, 4) among the SNPs in A1. At last, the likelihood ratio test is applied to the identified SNP set in hypothesis testing: it uses the difference between the deviance of the full d*-way logistic regression interaction model and the deviance of the null logistic regression model. Here we first use LR rather than MDR, because the null distributions of LR are known analytically. For 2, 3, 4-way full logistic regression interaction models, the null distributions follow χ2 distributions with df = 8, 26, 80, respectively. The experiment results are present in the upper panel of Figure 4. We can see that the obtained null distributions of logistic regression models match the theoretical null distributions well for 2, 3-way interaction models. For the 4-way interaction model, the estimated null distribution has a smaller degree of freedom than the theoretical null distribution. This is because about 666 samples are not enough to accurately estimate the large degree of freedom of the theoretical null distribution (df = 80). This is a disadvantage of using an independent data set for testing. When there are not enough samples, testing on an independent data set may have a lower power if its theoretical null distribution is used (This is an opposite case of the one shown in Figure 1).
Null distributions of testing on the independent data set. We generate 500 null data sets. Each data set has 2000 samples and 2000 SNPs. We divide each data set into three subsets with nearly equal size. The first one is used for screening, the second one is for modeling and the third one is for hypothesis testing. The upper panel: Logistic regression (LR) is used in modeling. The degrees of freedom of the theoretical null distributions are df = 8,26,80 for 2,3,4-way interaction models, respectively. We see that the null distributions of LR match the theoretical null distributions well for 2,3-way interaction models. The resulting null distribution of the 4-way interaction model follows  Here df = 73.18 is smaller than the theoretical one (df = 80) because there are only about 666 samples in hypothesis testing. The number of samples is too small to accurately estimate the large degree of freedom of the theoretical null distribution (df = 80). The lower panel: MDR is used in modeling. We can see that the obtained null distributions are roughly the same with those shown in the upper panel of Figure 2.
Here df = 73.18 is smaller than the theoretical one (df = 80) because there are only about 666 samples in hypothesis testing. The number of samples is too small to accurately estimate the large degree of freedom of the theoretical null distribution (df = 80). The lower panel: MDR is used in modeling. We can see that the obtained null distributions are roughly the same with those shown in the upper panel of Figure 2.
To see the effect of MDR using the independent data set in hypothesis testing, we similarly divide each null data set into three subsets: D(1), D(2), D(3). ReliefF is applied to D(1) and then MDR is applied to D(2). At last, χ2 tests are conducted on D(3) using the 2 × 2 contingency tables obtained by the MDR method. The result is shown in the lower panel of Figure 4. We can see that the obtained null distributions of MDR agree with the distributions shown in the upper panel of Figure 2. This result clearly shows that the null distributions are not changed by screening and modeling when testing on the independent data set.
Real data analysis using the suggested solutions: an experiment on the Aged-related Macular Degeneration (AMD) data set
We use the AMD data from [37] as a real example. The AMD study genotyped 116,204 SNPs on 96 cases and 50 controls. After applying quality control to the AMD data set, we have 82,143 qualified SNPs. Two significant loci, rs380390 and rs1329428, were reported in [37] based on the allelic association test with degree of freedom df = 1.
First, we use the latest MDR software to analyze this data set. ReliefF is applied to reduce the number of SNPs in AMD data from L = 82, 143 to d = 20. After that, MDR is applied to the remaining 20 SNPs to search for the best model. The result is given in Table 2. The AMD data set is available at http://bioinformatics.ust.hk/NullDistrAMD.zip. Our analysis result given in Table 2 can be freely reproduced. Following the typical selection procedure of MDR, the four-way interaction (i.e., model M4)among SNPs (rs1535891, rs2828151, rs404569, rs380390) is considered as the best one. If the effect of screening and modeling on changing the null distribution is not taken into account, then the hypothesis testing on M4 using the null distribution  (see the upper panel of Figure 2 (d = 4)) will give a P-value of 4.226 × 10–7, which is a significant result.
(see the upper panel of Figure 2 (d = 4)) will give a P-value of 4.226 × 10–7, which is a significant result.
Second, we use the permutation test to re-examine the above result. We conducted B = 500 permutations to the AMD data set. The details are given in the method section. The result is shown in Figure 5. The P-value obtained by the permutation test for model M4 is 0.1480, which is far from being significant. More importantly, the permutation result shows that model M1 is significant with P-value 0.0040. This result is consistent with that in the original paper [37].
Null distributions obtained using the permutation test. We conduct B = 500 permutations for the AMD data set, as described in the method section. The P-values obtained by the permutation test for models M1, M2, M3, M4 are 0.0040, 0.1180, 0.2880 and 0.1480, respectively. Only model M1 is significant. The claim of the significance of the high order interaction (rs1535891, rs2828151, rs404569, rs380390) based on Model M4 in Table 2 is inappropriate.
Third, we apply testing on the independent data set. The whole data set is partitioned into three groups (49, 49 and 48 individuals, respectively). ReilefF, MDR and hypothesis testing are sequentially applied to them, as described in the method section. Finally, no significant features are reported. This seems different from the result of the permutation test. The reason is that testing on the independent data set has a lower power than the permutation test. The number of samples of the AMD data set is very small (146 individuals). After a nearly equal partition of the data set, only 48 samples can be used in hypothesis testing. Thus no significant results can be detected (see more explanations in the simulation study section). Since the permutation test often has a higher power, the permutation test is preferred when the computational cost is affordable.
Discussion
The importance of hypothesis testing in feature assessment
It is important to note that hypothesis testing plays a key role in feature assessment [22, 23]. Model selection is a closely related topic, which aims to identify the best model in term of the prediction accuracy [22]. Analytical methods such as Akaike information criterion (AIC), Bayesian information criterion (BIC) can be applied for model selection. Efficient sample re-use methods such as cross-validation and bootstrapping can be applied here as well. However, to statistically quantify the importance of selected features, feature assessment is preferred. Instead of considering prediction accuracy, feature assessment makes use of hypothesis testing to statistically assess the significance of features. To characterize the performance of hypothesis testing, different measures have been defined, e.g., the family wise error rate (FWER) and the false discovery rate (FDR) [35, 36]. The Bonferroni correction and the Benjamini-Hochberg method [38] can be used for controlling FWER and FDR, respectively.
As pointed out by Efron [23], the choice of null distribution is critical in hypothesis testing. The empirical null distribution may not match the theoretical null distribution due to reasons such as inappropriate assumptions or correlation across features and samples. This paper shows that screening (e.g, ReliefF) and modeling (e.g, MDR) can also change the null distribution. If their effect is not taken into account in hypothesis testing, the resulting feature assessment will be unreliable.
Related work
We have shown that inappropriate choice of null distributions will give misleading results of hypothesis testing. One example is that MDR combined with Tuning ReliefF [6, 21] will give over-optimistic results. Alternatively, some other methods [25–27], which modify the test statistic but stick to the theoretical null distribution, may produce conservative results. For example, Machini et. al [25] proposed a two-stage method for detecting interactions in genome-wide scale. In the first stage, a single-locus-based test was performed. Those SNPs with significant P-values (i.e., smaller than a certain threshold α) were selected. The selected set of SNPs was denoted as I1 (I1 ⊂ {1,…, L}). In the second stage, for each pair of SNPs l and m (l, m ∈ I1, l ≠ m), the log likelihood ratio statistic R(l, m) was calculated for the full interaction model. They defined a new statistic R′(l, m) = R(l, m) – (k
l
+ k
m
), where k
l
and k
m
were the single-locus χ2 values for SNPs l and m. The significance of this statistic was assessed against  distribution, where df = 8 is the degrees of freedom of the full model fitted at the two SNPs. They showed that their method was conservative in term of the false positive rate. In fact, the modified statistic R′(l, m) is a shrunken version of R(l, m), but hypothesis testing is performed using the degree of freedom of R(l, m), where l, m ∈ {1,…, L}, l ≠ m. Thus, this method will be too conservative to detect interesting interactions.
distribution, where df = 8 is the degrees of freedom of the full model fitted at the two SNPs. They showed that their method was conservative in term of the false positive rate. In fact, the modified statistic R′(l, m) is a shrunken version of R(l, m), but hypothesis testing is performed using the degree of freedom of R(l, m), where l, m ∈ {1,…, L}, l ≠ m. Thus, this method will be too conservative to detect interesting interactions.
Conclusion
GWAS have identified many genomic regions associated with complex diseases. However, some previously reported results are based on an inappropriate choice of null distributions, which will produce many false positive results. In this work, we have illustrated that both screening and modeling can change the null distribution used in hypothesis testing. This causes unreliable significance assessment. We have suggested two solutions to address this issue. One is to use the permutation test and another is to use the independent data set for testing. Both solutions can help to appropriately choose null distributions, while the permutation test has a higher power with more computational cost.
Method
The null distribution is changed after the screening step and the modeling step in the stage-wise procedure. In this section, we suggest two solutions to address this issue. The first solution is to use the permutation test, which uses the re-sampling to generate the reference distribution for hypothesis testing. The second one is to use the independent data set for testing, which reserves the theoretical null distribution.
Suppose we have L SNPs and n samples for an association study. The whole data set D = [X; Y] is an (L + 1) × n matrix, where we use X to denote all SNPs with the l-th column X l corresponding to the l-th SNP, and use Y to denote the phenotype.
Permutation test
Since the screening step and the modeling step can change the null distribution, using theoretical null distribution in hypothesis testing may produce biased statistics, which will lead to a high false positive rate. The permutation test can generate the correct null distribution which has accounted for the effects of screening and modeling. This null distribution can be directly used in hypothesis testing. Specifically, the permutation test is done in the following steps:
-
1.
Compute the test statistic based on original data. Apply an efficient screening method to D and reduce it to D′, where D′ is a (d + 1) × n matrix collecting the top d features. Next, apply modeling methods such as MDR to D′ to identify the best model f(X*), where X* has d* features. Then calculate the test statistic of model f(X*) based on all samples, denoted as t obs .
-
2.
Generate B independent vectors Y(1),…, Y(B) by randomly permuting the response variable Y. Evaluate the permuted statistic T(b) of the same procedure in Step 1 corresponding to the permuted data set D(b) = [X; Y(b)], b = 1,…,B.
-
3.
Calculate the P-value as
 (1)
(1)
where I(·) is the indicator function.
In theory, a larger number of permutations will produce more accurate estimation. In practice, we typically use between 200 and 1000 permutations due to the high computational cost in the permutation test.
Testing on the independent data set
Screening and modeling pre-use the data that will be used in hypothesis testing. This leads to the change of the null distribution. Using an independent data set in hypothesis testing will avoid the change of the null distribution. It is particularly useful for those methods having analytic null distributions, for example, the likelihood ratio test for logistic regression models. This method consists of the following steps and it is also illustrated in Figure 6.
The procedure of using independent data sets in hypothesis testing. The whole data set D is partitioned into three subsets: D(1), D(2) and D(3). A screening method is applied to D(1). After screening, only a subset of features survives, denoted as A1. Then modeling methods are applied to D(2), but only involving the features in A 1 . This modeling process may further select a subset of features from A1, denoted as A2. Thus, A2 ⊂ A1. For feature assessment, hypothesis testing is applied to the features in A2 using the data set D(3). The correction factor for multiple testing is calculated based on the size of A2. After feature assessment, the significant features are collected in A3 and A3 ⊂ A2. They are finally used for genetic mapping.
-
1.
Partition the whole data set D into three subsets with nearly equal size: D(1), D(2) and D(3).
-
2.
Apply an efficient screening method to D(1) and identify a subset of features, denoted as A1. Let |A1| denote the size of A1 and we have |A1| ⊈ L.
-
3.
Apply a modeling method to D(2) by only involving the features in A1. The identified features are collected in A2 and we have A2 ⊂ A1.
-
4.
Perform hypothesis test on the features in A2 using the data set D(3). The correction factor for multiple testing can be calculated based on |A2|. The detected significant features are collected in A 3 and A3 ⊂ A2. These features are finally used for genetic mapping.
This solution can be applied without sacrificing the running time. However, it has a requirement on the number of samples. A small sample size will degrade its performance. In that situation, the permutation test is a better choice.
References
WTCCC: Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature 2007, 447: 661–678. 10.1038/nature05911
Balding D: A tutorial on statistical methods for population association studies. Nature Reviews Genetics 2006, 7: 781–791. 10.1038/nrg1916
Eichler E, Flint J, Gibson G, Kong A, Leal S, Moore J, Nadeau J: Missing heritability and strategies for finding the underlying causes of complex disease. Nature Reviews Genetics 2010, 11(6):446–450. 10.1038/nrg2809
Cordell H: Detecting gene-gene interactions that underlie human diseases. Nature Reviews Genetics 2009, 10: 392–404. 10.1038/nrg2579
Nelson M, Kardia S, Ferrell R, Sing C: A combinatorial partitioning method to identify multilocus genotypic partitions that predict quantitative trait variation. Genome Research 2001, 11(3):458. 10.1101/gr.172901
Ritchie M, Hahn L, Roodi N, Bailey L, Dupont W, Parl F, Moore J: Multifactor-dimensionality reduction reveals high-order interactions among estrogenmetabolism genes in sporadic breast cancer. Am J Hum Genet 2001, 69: 138–147. 10.1086/321276
Phillips PC: Epistasis-the essential role of gene interactions in the structure and evolution of genetic systems. Nature Reviews Genetics 2008, 9(11):855–867. 10.1038/nrg2452
Culverhouse R, Klein T, Shannon W: Detecting epistatic interactions contributing to quantitative traits. Genetic Epidemiology 2004, 27: 141–152. 10.1002/gepi.20006
Zheng T, Wang H, Lo S: Backward genotype-trait association (BGTA) - based dissection of complex traits in case-control design. Human Heredity 2006, 62: 196–212. 10.1159/000096995
Wan X, Yang C, Yang Q, Xue H, Tang N, Yu W: Predictive rule inference for epistatic interaction detection in genome-wide association studies. Bioinformatics 2010, 26: 30–37. 10.1093/bioinformatics/btp622
Tibshirani R: Regression shrinkage and selection via the Lasso. Journal of the Royal Statistical Society, series B 1996, 58: 267–288.
Wu T, Chen Y, Hastie T, Sobel E, Lange K: Genomewide Association Analysis by Lasso Penalized Logistic Regression. Bioinformatics 2009, 25(6):714–721. 10.1093/bioinformatics/btp041
Yang C, Wan X, Yang Q, Xue H, Yu W: Identifying main effects and epistatic interactions from large-scale SNP data via adaptive group Lasso. BMC Bioinformatics 2010, 11(Suppl 1):S18. 10.1186/1471-2105-11-S1-S18
Chen X, Liu C, Zhang M, Zhang H: A forest-based approach to identifying gene and gene-gene interactions. Proceedings of the National Academy of Sciences of the United States of America 2007, 104(49):19199–19203. 10.1073/pnas.0709868104
Wan X, Yang C, Yang Q, Xue H, Fan X, Tang N, Yu W: BOOST: A fast approach to detecting gene-gene interactions in genome-wide case-control studies. Am J Hum Genet 2010, 87(3):325–340. 10.1016/j.ajhg.2010.07.021
Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira M, Bender D, Maller J, Sklar P, De Bakker P, Daly M, et al.: PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet 2007, 81(3):559–575. 10.1086/519795
Zhang Y, Liu J: Bayesian inference of epistatic interactions in case-control studies. Nature Genetics 2007, 39: 1167–1173. 10.1038/ng2110
Yang C, He Z, Wan X, Yang Q, Xue H, Yu W: SNPHarvester: a filtering-based approach for detecting epistatic interactions in genome-wide association studies. Bioinformatics 2009, 25(4):504–511. 10.1093/bioinformatics/btn652
Herold C, Steffens M, Brockschmidt F, Baur M, Becker T: INTERSNP: genome-wide interaction analysis guided by a priori information. Bioinformatics 2009, 25(24):3275–3281. 10.1093/bioinformatics/btp596
Moore J, Asselbergs F, Williams S: Bioinformatics challenges for genome-wide association studies. Bioinformatics 2010, 26(4):445–455. 10.1093/bioinformatics/btp713
Moore J, White B: Tuning ReliefF for genome-wide genetic analysis. Lecture Notes in Computer Science, Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics 2007, 4447: 166–175. full_text
Hastie T, Tibshirani R, Friedman J: The Elements of Statistical learning: Data Mining, Inference, and Prediction. 2nd edition. NewYork: Springer; 2009.
Efron B: Large-scale simultaneous hypothesis testing: The choice of a null hypothesis. Journal of the American Statistical Association 2004, 99(465):96–104. 10.1198/016214504000000089
Niu A, Zhang Z, Sha Q: Application of seventeen two-locus models in genome-wide association studies by two-stage strategy. BMC Proc 2009, 3(Suppl 7):S26. 10.1186/1753-6561-3-s7-s26
Marchini J, Donnelly P, Cardon LR: Genome-wide strategies for detecting multiple loci that influence complex diseases. Nature Genetics 2005, 37(4):413–417. 10.1038/ng1537
Evans D, Marchini J, Morris A, Cardon L: Two-stage two-locus models in genome-wide association. PLoS Genetics 2006, 2(9):e157. 10.1371/journal.pgen.0020157
Med B: Optimal two-stage strategy for detecting interacting genes in complex diseases. BMC Genetics 2006, 7: 39.
Kira K, Rendell L: A practical approach to feature selection. Proceedings of the Ninth International Workshop on Machine learning 1992, 249–256.
Wiskott L, Fellous J, Kruger N, Malsburg C: Estimating attributes: analysis and extension of relief. European Conference on Machine Learning 1994, 171–182.
Greene C, Himmelstein D, Kiralis J, Moore J: The informative extremes: using both nearest and farthest individuals can improve Relief algorithms in the domain of human genetics. Lecture Notes in Computer Science, Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics 2010, 6023: 182–193. full_text
Park M, Hastie T: Penalized logistic regression for detecting gene interactions. Biostatistics 2008, 9: 30–50. 10.1093/biostatistics/kxm010
Hastie T, Tibshirani R: Generalized additive models. Chapman & Hall/CRC; 1990.
Li W, Yang Y: Fractal Characterizations of MAX Statistical Distribution in Genetic Association Studies. Advances in Complex Systems (ACS) 2009, 12(04):513–531. 10.1142/S0219525909002349
Greene C, Penrod N, Kiralis J, Moore J: Spatially Uniform ReliefF (SURF) for computationally-efficient filtering of gene-gene interactions. BioData Mining 2009, 2: 5. 10.1186/1756-0381-2-5
Dudoit S, Laan M: Multiple Testing Procedures with Applications to Genomics. Springer; 2008.
Dudoit S, Shaffer J, Boldrick J: Multiple hypothesis yesting in microarray experiments. Statistical Science 2003, 18: 71–103. 10.1214/ss/1056397487
Klein R, Zeiss C, Chew E, Tsai J, Sackler R, Haynes C, Henning A, SanGiovanni J, Mane S, Mayne S, Bracken M, Ferris F, Ott J, Barnstable C, Hoh J: Complement factor H polymorphism in age-related macular degeneration. Science 2005, 308: 385–389. 10.1126/science.1109557
Benjamini Y, Hochberg Y: Controlling the false discovery rate: a practical and powerful approach to multiple teting. Journal of the Royal Statistical Society Series B 1995, 85: 289–300.
Acknowledgement
This work was partially supported with the grant GRF621707 from the Hong Kong Research Grant Council, the grants RPC06/07.EG09, RPC07/08.EG25 and RPC10EG04 from HKUST, the Natural Science Foundation of China under Grant No. 61003176, and the Fundamental Research Funds for the Central Universities of China (DUT10JR05 and DUT10ZD110).
This article has been published as part of BMC Bioinformatics Volume 12 Supplement 1, 2011: Selected articles from the Ninth Asia Pacific Bioinformatics Conference (APBC 2011). The full contents of the supplement are available online at http://www.biomedcentral.com/1471-2105/12?issue=S1.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
CY and XW contributed equally to this work. They conducted all experiments. CY, XW and ZH drafted the manuscript together. QY, HX and WY initialized this work. WY finalized the manuscript. All authors read and approved the final manuscript.
Rights and permissions
This article is published under license to BioMed Central Ltd. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yang, C., Wan, X., He, Z. et al. The choice of null distributions for detecting gene-gene interactions in genome-wide association studies. BMC Bioinformatics 12 (Suppl 1), S26 (2011). https://doi.org/10.1186/1471-2105-12-S1-S26
Published:
DOI: https://doi.org/10.1186/1471-2105-12-S1-S26






