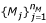- Research article
- Open access
- Published:
A normalization strategy applied to HiCEP (an AFLP-based expression profiling) analysis: Toward the strict alignment of valid fragments across electrophoretic patterns
BMC Bioinformatics volume 6, Article number: 43 (2005)
Abstract
Background
Gene expression analysis based on comparison of electrophoretic patterns is strongly dependent on the accuracy of DNA fragment sizing. The current normalization strategy based on molecular weight markers has limited accuracy because marker peaks are often masked by intense peaks nearby. Cumulative errors in fragment lengths cause problems in the alignment of same-length fragments across different electropherograms, especially for small fragments (< 100 bp). For accurate comparison of electrophoretic patterns, further inspection and normalization of electrophoretic data after fragment sizing by conventional strategies is needed.
Results
Here we describe a method for the normalization of a set of time-course electrophoretic data to be compared. The method uses Gaussian curves fitted to the complex peak mixtures in each electropherogram. It searches for target ranges for which patterns are dissimilar to the other patterns (called "dissimilar ranges") and for references (a kind of mean or typical pattern) in the set of resultant approximate patterns. It then constructs the optimal normalized pattern whose correlation coefficient against the reference in the range achieves the highest value among various combinations of candidates. We applied the procedure to time-course electrophoretic data produced by HiCEP, an AFLP-based expression profiling method which can detect a slight expression change in DNA fragments. We obtained dissimilar ranges whose electrophoretic patterns were obviously different from the reference and as expected, most of the fragments in the detected ranges were short (< 100 bp). The normalized electrophoretic patterns also agreed well with reference patterns.
Conclusion
The normalization strategy presented here demonstrates the importance of pre-processing before electrophoretic signal comparison, and we anticipate its usefulness especially for temporal expression analysis by the electrophoretic method.
Background
Amplified fragment length polymorphism (AFLP) is a DNA fingerprinting technique using electropherograms [1]. AFLP analysis belongs to the category of selective restriction fragment amplification techniques, which are based on the ligation of adapters to genomic restriction fragments followed by PCR-based amplification with adapter-specific primers [2]. This technique has been widely used for genotyping since it requires no prior knowledge of genomic DNA sequences and offers potentially better discriminatory power and speed than the existing techniques for fingerprinting such as random-amplified polymorphism DNA markers (RAPD) [3–8]. However, it has only been used to a limited extent for expression analysis [9]. The main problems with the comparison of AFLP patterns are (i) variation in peak height, and (ii) false positive peaks which often overlap with real peaks, probably due to differences in PCR efficiency [5, 10]. There is room for tuning selective PCR amplification [8].
Recently, we developed an AFLP-based gene expression profiling method called HiCEP (High Coverage Expression Profiling) [11]. The experimental and analytical procedures are essentially the same as those of AFLP, i.e., the technique is based on the selective PCR amplification of restriction fragments from a total restriction digest of genomic DNA. Refinements of the selective PCR technique improved reproducibility and reduced the rate of false positive peaks as well as the number of peaks. They also enabled the digestion of purified genomic DNA with two four-nucleotide recognition restriction enzymes, having a higher cutting frequency, such as Msp I and Mse I. Consequently, the HiCEP method can detect a slight expression change of transcript-derived fragments (TDFs) with high coverage. The estimated 30,000 transcripts expressed in a cell are divided into 256 subgroups (16 MspI-NN primers * 16 NN-MseI primers) containing approximately 120 PCR-amplified TDFs. This number is small enough to be separated by fluorescent capillary electrophoresis using an automated DNA sequencer such as the ABI Prism 310 (Applied Biosystems). We can achieve higher throughput by using several fluorescent dyes at once [14, 15].
Normally, digitized electropherograms are imported into image analysis software such as GeneScan (Applied Biosystems), which outputs each fragment (band) together with its length (in bp), area and height (signal intensity), carrying out accurate fragment sizing and background subtraction for most of the operations. GeneScan is capable of separating the signal from each fluorophore to provide higher throughput analysis. However, it should be noted that intense signals from abundant TDFs can breed into each other, potentially confusing the fragment sizing [7, 15]. Furthermore, the use of a frequently matching 4-bp cutting endonuclease (Mse I) tends to produce many small TDFs (< 100 bp) and in our experience this range is prone to errors of fragment sizing. Cumulative errors of fragment sizing interfere with normalization across different electropherograms and lead to the mis-assignment of valid TDFs. Hence, more detailed analysis such as observation of gradual expression changes in the time series of a TDF still counts in subjective visual examination [11]. Further preprocessing of the electrophoretic data to be compared, each of which is independently normalized according to molecular weight standards, is needed.
The purpose of the present study is to develop a normalization method for the automated analysis of temporal electrophoretic data. We assume the samples to be compared are identical, that TDFs have similar fragment lengths across electropherograms and that expression changes can be detected as variations in peak height using the HiCEP technique. The performance of the method is demonstrated by analyzing a large set of time-course data obtained from mouse embryonic stem (ES) cells, using HiCEP.
Results and discussion
We analyzed a total of 2560 HiCEP electropherograms (256 sets of ten), containing time-course data of embryonic stem (ES) cells 0, 12, 24, 48, and 96 h after adding stimulation for differentiation. Reproducibility was confirmed by the duplication. We applied the current method to each of the 256 sets.
Delineation of quality profiles for lanes
When a set of electrophoretic data is arranged and surveyed, one can often find ranges (called 'dissimilar ranges') in which peak fragment lengths are incorrectly measured. For example, in Fig. 1a three lanes (0 h-1, 12 h-1, and 48 h-2) in the range (35–50 bp) appear to be compressed on the short side. This is probably because another intense peak just under 35 bp is mistaken for the 35 bp marker peak. This reduces the overall similarity between lanes and makes it difficult to recognize identical TDFs such as red filled peaks in Fig. 1a.
Electrophoretic patterns and the quality profiles for ten lanes from a primer combination of CT-tt. Samples are mouse embryonic stem (ES) cells 0, 12, 24, 48, and 96 h after differentiation. There are ten lanes since each sample are duplicated. From bottom to top: 0 h-1, 0 h-2, 12 h-1, 12 h-2, 24 h-1, 24 h-2, 48 h-1, 48 h-2, 96 h-1, and 96 h-2. Data from a primer combination of CT-tt in the interesting range (35–102 bp) are shown. (a) The approximated electrophoretic lane data and, (b) its interpolated quality profile. An example of calculation of quality profiles for lane 0 h-1 is shown in Table 1. Note the variation in the lengths of particular TDFs across peaks of lanes (red filled peaks).
To this end, we first developed a method for displaying dissimilar ranges. The method is based on a moving-fragment approach that continuously determines the average correlation coefficient between particular lane Ptargetand the other lanes within a certain range using equation 3. By using the average correlation coefficients, we can make a quality score function Qk(t) for all lanes (k = 1, 2, ..., 10) at arbitrary length t (see Methods). An example of the calculation for lane 0 h-1 is shown in Table 1. The 'quality profiles' delineated from Q(t) take the place of detailed visual evaluation of dissimilar ranges (Fig. 1b). Undoubtedly, false peaks must have been used incorrectly at 35 bp in three lanes (0 h-1, 12 h-1, and 48 h-2) and at 75 bp in two lanes (0 h-2 and 96 h-1).
Detection of dissimilar ranges
Next, we applied a simple method for the automated detection of dissimilar ranges to 256 sets of electrophoretic data (see Method). The method identified a total of 362 dissimilar ranges. Most (289, 79.8%) of the ranges were of 100 bp or less. This is reasonable because the main source of fragment sizing errors is the presence of intense peaks near the marker [7, 11, 15] and the HiCEP technique tends to produce short fragments. In fact, of a total of 222,108 detected peaks in the range (35–700 bp) analyzed by GeneScan, 58,988 (26.6%) were < 100 bp.
Visual examination revealed many of those ranges to be genuine, but not all. The set of ten electropherograms shown in Fig. 1 is a good example. Our method identified seven ranges as dissimilar: five lanes (0 h-1, 0 h-2, 12 h-1, 12 h-2, and 48 h-2) in range (35–50 bp) and two lanes (0 h-2 and 96 h-1) in range (50–100 bp). Of these, we at first suspected that two lanes (0 h-2 and 12 h-2) in range (35–50 bp) were false-positives (mistakenly identified as dissimilar). However, we observed that the range in the two lanes is worthy of being normalized: the fragment lengths on the short side of the range deviate gradually from the mean lengths of lanes 24 h-1, 24 h-2, 96 h-1, and 96 h-2 [see Additional file 1].
Visual examination of all the electropherograms did not reveal any false-negative errors (overlooked dissimilar ranges). Recall that the samples to be compared are identical and that the measure of the quality of fragment sizing is based on a calculation of the average correlation between electropherograms. These results suggest that the normalization strategy we present here is useful, especially for temporal expression analysis.
The effectiveness of the method depends on the choice of the parameter T in equation 3 in the Methods section, which is the number of consecutive fragments making up the quality profile examined by the program. Quality profiles using the shortest span (T = 1) are noisier than those using a moderate span, and runs using spans of less than four fragments were found unsatisfactory in our investigation. On the other hand, long spans (T = 10) tended to miss small dissimilar ranges. These trends are essentially the same as those in the delineation of hydropathy plots of proteins using a moving-window approach and in the detection of transmembrane regions [16]. Although we set T = 5 throughout the analysis, further improvement in the choice of parameters as well as the method for the detection of dissimilar ranges remains to be studied.
Normalization of dissimilar ranges
To normalize dissimilar ranges across a set of electropherograms, it is necessary to select one as a reference. In conventional algorithms the reference is selected manually [17, 18]. For reproducible automated normalization, it is vital that the choice be objective. Our method selects the lane (electropherogram) having the highest average quality score in a given dissimilar range. In the case of Fig. 1, our method selects 96 h-2 as the best reference in ranges (35–50 bp) and (50–100 bp). We cannot, of course, reject the possibility that accurate fragment sizing is performed in the minority group (such as lanes 0 h-1, 12 h-1, and 48 h-2 in range (35–50 bp) in Fig. 1), but it is natural that the best reference should be selected from lanes in the majority group.
We prepared two models for accurate normalization of various types of fragment sizing errors. Model 1 is the case of an incorrect fragment sizing at the shortest (or longest) marker peak. Figure 2 shows an example of normalization using Model 1. The best approximating profile (normalized profile) is determined by considering various combinations of candidates from D × 100% expansion (or - D × 100% compression) to D × 100% compression of the short side of the original profile at intervals of d bp. The best approximating profile is one of the candidate profiles with {x × d - D × (C e - Cs)} / (C e - Cs) × 100% compression of the side in a given range (C s - C e bp), where x = {0, 1, ..., 2 × (C e - Cs) × D / d}. There is of course a trade-off between the computation time and the normalization accuracy in the choices of parameters. In Model 1, we set D = 0.4 and d = 0.2. We expected that the normalization would be achieved by a linear expansion of the short side of the dissimilar range (35–50 bp) by anchoring the long-side in the target lane 12 h-1. Indeed, the best approximating profile that achieved the highest correlation coefficient against the reference 96 h-2 was the case of x = 9 (28% expansion).
Normalization for lane 12 h-1 in dissimilar range (35–50 bp) in Fig. 1 (Model 1). Magnified expression profiles of the target 12 h-1 and the reference 96 h-2 in the range in Fig. 1 are shown (top). Colours are the same as those in Fig. 1. There are 61 possible combinations in this case: 30 different levels of expansion (x = 0, 1, ..., 29), the original target profile (x = 30), and 30 compressions (x = 31, 32, ..., 60). The highest correlation coefficient between the best approximating profile and the reference in range (3–-50 bp) was 0.844 for the case x = 9. The position of x on the X axis corresponds to the new position of the short side (originally, 35 bp) of the original profile after expansion or compression. For example, the new position of the short side after maximum expansion (x = 0) becomes 29 bp, while after maximum compression (x = 60) it becomes 41 bp. Visual evaluation of three representative approximate profiles (x = 0, 9, and 60) in range (35–50 bp) confirmed the validity of the normalization (bottom).
Figure 3 shows an example of normalization using Model 2. Model 2 is the case of an incorrect fragment sizing at the marker length M j in a dissimilar range (Mj-1-Mj+1bp) (see Methods). Accordingly, the program can easily determine the length of 75 bp because there is only one marker length inside of the range (50–100 bp). We can directly apply the normalization procedure for Model 1 to Model 2 by considering two hypothetical dissimilar ranges, (50–75 bp) and (75–100 bp). The main difference from Model 1 is that the two ranges cannot be normalized independently in Model 2: {x × d - D × (100 - 50)}/(100 - 50) × 100% compression (resp. expansion) of the long-side of the original profile in range (50–75 bp) and {x × d - D × (100 - 50)}/(100 - 50) × 100% expansion (resp. compression) of the short side in range (75–100 bp) affect on each other. In Model 2, we set D = 0.1 and d = 0.2 as a maximal realistic displacement. The best approximating profile is the case of x = 13 and is consistent with the reference profile.
Normalization for lane 0 h-2 in the dissimilar range (50–100 bp) in Fig. 1 (Model 2). Magnified expression profiles of the target 0 h-2 and the reference 96 h-2 in range (50–100 bp) are shown (top). Colours are the same as those in Fig. 1. There are 51 possible combinations in this case. The highest correlation coefficient between the best approximating profile and the reference in the range (50–100 bp) was 0.911 for the case x = 13. Visual evaluation of three representative approximate profiles (x = 0, 13, and 50) in the range confirmed the validity of the normalization (bottom).
Figure 4 shows the result of normalization for electrophoretic patterns in the primer combination of Fig. 1. Seven dissimilar ranges (coloured in red; five in range (35–50 bp) and two in range (50–100 bp); 0 h-2 has two normalized ranges) are normalized nearly perfectly (Fig. 4a). For example, the electrophoretic pattern of 0 h-2 in range (35–50 bp) which is a possible false-positive error are normalized as 2.7% compression of a short side of the range. The correlation coefficients between the target 0 h-2 and the reference 96 h-2 in the range before and after normalization are 0.674 and 0.798, respectively.
Electrophoretic patterns and the quality profiles after normalization in Fig. 1. (a) Normalized electrophoretic patterns. Ranges coloured in red were detected as dissimilar and normalized. Note that the 0 h-2 consists of two dissimilar ranges: (35–50 bp) and (50–100 bp). After normalization the valid (red filled) peaks are much closer together. (b) Consequently, the more accurate fragment lengths and peak areas in the ranges are accompanied by an increase in the quality scores.
A quality profile for lane 48 h-2 indicates that an incorrect normalization is performed in range (35–50 bp) of the lane. The low correlation coefficient (0.4) between the normalized profile and the reference 96 h-2 in the range, compared to values (> 0.7) between four other normalized profiles (0 h-1, 0 h-2, 12 h-1, and 12 h-2) and the reference in the corresponding range, strengthens this suspicion [see Additional file 2]. After visual examination it was decided that the dissimilar range (35–50 bp) of lane 48 h-2 should be extended on the long side. We searched for the best range to be normalized and chose (35–53.6 bp). The correlation coefficient of the normalized profile, expanded by 26.3% on the short side in the range (35–53.6 bp), was 0.9. Undoubtedly an exhaustive search for edges in dissimilar range might yield better normalization for some cases. However, it also dramatically increases the possible combinations of normalization candidates. It is a balance between the computation time and the number of analyzable TDFs.
One way to do objective evaluation of normalized electrophoretic patterns is to re-delineate the quality profiles (Fig. 4b). Generally, a higher quality score Qk(t) for lane k indicates greater consistency with the other lanes around arbitrary length t if the sample is identical (e.g., time-course data). The quality scores after normalization overall were higher than before (Figs. 1b and 4b). This means the assignments of the quality scores to time-course electrophoretic data are effective for evaluating reproducibility.
Evaluation of the method
The normalization method we propose here can be regarded as an image warping method which deforms images by mapping between image domains [19]. There are a number of reports on warping methods especially for dealing with two-dimensional (2-D) images [19–21]. There are also some methods for 1-D electrophoretic data [17, 18, 22]. Comparison with these methods might provide an objective evaluation of the current method. However, they are not directly comparable with the current method because of different frameworks such as input data format, the requirement of pre-determined parameters, and so on [17, 22].
A critical step in the analysis of 1-D electrophoretic data is the assignment of the correct size to each TDF. In time-course data, one expects that the same TDFs should have quite close fragment lengths across electropherograms and that temporal expression changes are reflected as differences in peak height. We developed the current method aimed at temporal expression analysis by the electrophoretic method and used a scoring system for an objective evaluation of experimental reproducibility using Qk(t) which indicates a relative similarity at t (bp) in lane k to the other lanes. We demonstrate two other sets of electrophoretic data and discuss the feasibility of the method.
Figure 5 shows a set of electrophoretic patterns and quality scores which is different from the primer combination used in Figs. 1, 2, 3, 4. This is a representative example of electrophoretic patterns with high quality scores (arbitrary defined as > 0.7). Visual evaluation confirmed the reproducibility of the set of ten electrophoretic patterns throughout the analyzed range (35–700 bp). There is, of course, no dissimilar range detected by the current method.
We should demonstrate the case of normalization to dissimilar range (35–75 bp) where both Models 1 and 2 are applicable. A set of ten electrophoretic patterns and their quality scores shown in Figure 6 is the good example. There are three lanes with dissimilar range (24 h-2, 48 h-2, and 96 h-1) detected by the method. Of these, 24 h-2 and 96 h-1 were normalized using Model 1 and 48 h-2 was normalized using Model 2. Visual evaluation of the electrophoretic patterns and the quality scores after normalization verified the choices of the models as appropriate (Figure 7). The use of normalized electrophoretic patterns facilitates the identification of TDFs (e.g., red filled fragments in Fig. 7) having potential temporal expression change. The development of a peak alignment algorithm for multiple lanes and integration with the current method are the next challenge.
Electrophoretic patterns and the quality profiles for ten lanes from a primer combination of GA-gc. Data from a primer combination of GA-gc in the interesting range (35–80 bp) are shown. (a) The electrophoretic data lane and (b) its quality profile. Three lanes (24 h-2, 48 h-2, and 96 h-1) have a dissimilar range (35–75 bp) suitable for both normalization Models 1 and 2.
We also estimated the feasibility of the method with regard to an increasing number of peaks with certain quality score or more. The minimum value of Q(t) necessary for the accurate alignment of valid TDFs across lanes is about 0.7 (Fig. 4b). Accordingly, we set the threshold to be 0.7. The number of peaks with Q(t) ≥ 0.7 in the range (35–700 bp) before and after normalization are 202,204 (91.0% of the total number of peaks in the range detected by GeneScan) and 205,829 (92.7%), respectively. Furthermore, 3,334 (92%) of the 3,625 (= 205,829 - 202,204) new high-quality peaks were < 100 bp, which corresponds to the biased distribution of the detected dissimilar ranges (nearly 80% of which were 100 bp or less).
Conclusion
When we apply the method to HiCEP time-course data, we assume that the set of electrophoretic data to be compared is identical (i.e., corresponding TDFs across electropherograms should have nearly the same fragment lengths). The monitoring of temporal expression change by the HiCEP technique has great potential for screening of genes related to chemotherapeutic drug resistance, circadian rhythm, and so on [11, 23, 24]. Although the current method was developed for pre-processing HiCEP data, the algorithm is easily applicable to the processing of other 1-D electrophoretic data such as AFLP and DD if the samples are identical or nearly identical. We strongly recommend the strategy be widely used for data processing for temporal expression analysis by the electrophoretic method.
Methods
Samples
mRNAs were prepared from mouse embryonic stem (ES) cells at 0, 12, 24, 48, and 96 h after removal of Leukemia Inhibitory Factor (LIF) from the culture medium. The samples subjected to HiCEP reaction were duplicated. We designated each sample as 0 h-1, 0 h-2, 12 h-1, 12 h-2, 24 h-1, 24 h-2, 48 h-1, 48 h-2, 96 h-1, and 96 h-2.
HiCEP analysis
mRNAs prepared from each sample were digested with two 4-bp-cutting endonucleases (Msp I combined with Mse I) and ligated with the corresponding adaptors. The resulting HiCEP templates, MspI-MseI-poly(A) mRNAs, were amplified by fluorescently labelled primers; for labelling, FAM, HEX, and NED were used. In total, 256 primer combinations (16 MspI-NN primers combined with 16 NN-MseI primers; N = {A, C, G, T}) were used in the HiCEP analysis. For example, a primer combination of MspI-TA and GC-MseI is capable of amplifying particular transcript-derived fragments (TDFs) corresponding to that combination. The details of the protocol of the HiCEP reaction are described elsewhere [11]. An animation of the principle is provided at the following URL http://133.63.22.11/english/research/serch03.html.
Electrophoresis and image analysis
The PCR products were denatured and loaded on an ABI Prism 310 (Applied Biosystems) for capillary gel electrophoresis. The digitized images were analyzed by the GeneScan software (Applied Biotech). The size of the fragments was calculated by the software, according to internal molecular size markers of 35, 50, 75, 100, 139, 150, 160, 200, 300, 340, 350, 400, 490, 500, 600, and 700 bp, on each gel. The fragment sizing and baseline subtraction were performed by the software. The software quantifies each peak by the fragment length L (in bp), peak height H, and area A (in arbitrary units). Accordingly, the subsequent normalization procedure accepts these three-tuples as input for detected TDFs between 35 bp and 700 bp. TDFs smaller than 35 bp or larger than 700 bp were omitted from the analysis because the range was outside the size calibration range.
Delineation of quality scores for lanes
The starting point of normalization is a set of lanes (10 time-course measurements; 0, 12, 24, 48, and 96 h, each experiment duplicated) in each of 256 primer combinations. We explain the procedure using data from the primer combination of 'Msp I-CT combined with tt-Mse I (designated as CT-tt)' because the ten electropherograms have some ranges for which fragment sizing is obviously inappropriate (we therefore designated such ranges as "dissimilar ranges").
The first step starts from the Gaussian approximation of each lane. The use of the approximating lane is the same as described in Aittokallio et al. [25–27]. Briefly, a fragment F
i
in lane P is originally characterized by the three-tuples (L
i
, H
i
, A
i
). If lane P consists of n fragments  , the approximation of the lane at length t is given by:
, the approximation of the lane at length t is given by:

where σ i is obtained from the following equation:

The approximation is performed independently for each lane. The ten approximate profiles of time-course data in the primer combination of CT-tt are shown in Fig. 1a.
For the automated identification of 'dissimilar ranges' from the expression profiles of ten lanes

, we next assign quality scores to each of the fragments  , where the fragments are originally numbered with respect to their lengths. By using the ten approximate profiles, relative similarity scores
, where the fragments are originally numbered with respect to their lengths. By using the ten approximate profiles, relative similarity scores  for intervals from fragment i to fragment (i+T-1) (i = 1, 2,..., n - T + 1) in lane Ptarget(target = {1, ..., 10}) are calculated from the following equation:
for intervals from fragment i to fragment (i+T-1) (i = 1, 2,..., n - T + 1) in lane Ptarget(target = {1, ..., 10}) are calculated from the following equation:

where

is the Pearson correlation coefficient between the target lane Ptargetand one of the other lanes Pkin the interval (start-end bp) which always includes T fragments from fragment i to fragment (i+T-1) (i = 1, 2, ..., n-T+1). The interval is defined as: start = L
i
- 2.5σ
i
and end = Li+T-1+ 2.5σi+T-1. In this analysis, the number of fragments T is held constant at T = 5; other numbers are of course possible. By applying a moving window of T fragments, most of the fragments (n-T+2 fragments in this case, with the exception of F1, F2, F3, F4, Fn-3, Fn-2, Fn-1, and F
n
) have T relative similarity scores. Finally, the relative quality value Q(L
i
) for fragment F
i
is defined as the average of the similarity scores which satisfy start ≤ L
i
≤ end. An example of the calculation is given in Table 1. Quality scores at arbitrary lengths t, Q(t), are interpolated by the use of cubic splines to  . The procedure is applied to each of the ten lanes
. The procedure is applied to each of the ten lanes  and then the quality profiles
and then the quality profiles  corresponding to the expression profiles are created (Fig. 1b).
corresponding to the expression profiles are created (Fig. 1b).
The quality profiles delineated from Q(t) have a clear interpretation. The high (or low) score for Qk(t) in lane k indicates a high (or low) level of relative similarity between the lane and the others around the length t.
Detection of dissimilar ranges
Now we have information (quality profiles) for the automated detection of dissimilar ranges. Here we adopt a simple method for detecting the range. Briefly,
-
1)
Seek 'seed' ranges (C seed_s - C seed_e bp) which satisfy two conditions: a) Q(t) ≤ thres seed and b) they contain at least two peaks.
-
2)
Seek C tmp_s which satisfies both
 and C
tmp_s
<C
seed_s
; similarly, C
tmp_e
,
and C
tmp_s
<C
seed_s
; similarly, C
tmp_e
,  and C
tmp_e
<C
seed_e
and C
tmp_e
<C
seed_e
-
3)
Substitute the nearest marker length
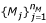
(in this case, M1 = 35, M2 = 50, ...,
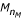 = 700) to C
tmp_s
(resp. C
tmp_e
) for C
s
(resp. C
e
); accordingly, both C
s
and C
e
=
= 700) to C
tmp_s
(resp. C
tmp_e
) for C
s
(resp. C
e
); accordingly, both C
s
and C
e
= 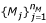 and C
s
<C
e
and C
s
<C
e
Aparameter thres seed is set to 0.3 empirically. Forexample, P9 has the following parameters in Fig. 1b: C seed_s = 57.04, C seed_e = 89.98, C tmp_s = 52.60, C tmp_e = 104.60, C s = M2, and C e = M4. Although fine tuning might be necessary, the procedure enables us to display dissimilar ranges.
Selection of the reference lane
When we want to correct a dissimilar range (C
s
- C
e
bp), we have to select the "reference" (a kind of mean or typical profile in the corresponding range). One method is to choose lane Preferencesatisfying max { }, where
}, where  is the average of Qkin the range (C
s
- C
e
bp) in lane
is the average of Qkin the range (C
s
- C
e
bp) in lane  . For example, the algorithm selects P10 (i.e., 96 h-2) as a reference in a particular range (M1-M2 bp) and also in range (M2-M4 bp).
. For example, the algorithm selects P10 (i.e., 96 h-2) as a reference in a particular range (M1-M2 bp) and also in range (M2-M4 bp).
Two models for the normalization of dissimilar ranges
The meaning of the word "normalization" here is to correct the fragment lengths (L) and the areas (A) of peaks in a dissimilar range so that the similarity between the normalized electrophoretic pattern and the reference pattern in the corresponding range can be maximized. To normalize a particular lane Ptargetagainst the reference Preference, we now consider the following two models. Model 1 is the case of an incorrect fragment sizing at the shortest (or longest) marker peak, i.e, C
s
= M1 = 35 (or C
e
= 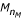 = 700). The peak lengths deviate more and more from the reference length moving from C
e
to C
s
(or from C
s
to C
e
). Model 2 is the case of an incorrect fragment sizing near marker length M
j
(C
s
<M
j
<C
e
, j = {2, 3,..., n
M
- 1}; the inside of dissimilar range (C
s
- C
e
bp)). Roughly, the deviation of peak lengths from the reference length gradually increases starting from C
s
; the maximum deviation is reached at M
j
(C
s
<M
j
<C
e
); the deviation decreases gradually; and finally disappears at C
e
bp.
= 700). The peak lengths deviate more and more from the reference length moving from C
e
to C
s
(or from C
s
to C
e
). Model 2 is the case of an incorrect fragment sizing near marker length M
j
(C
s
<M
j
<C
e
, j = {2, 3,..., n
M
- 1}; the inside of dissimilar range (C
s
- C
e
bp)). Roughly, the deviation of peak lengths from the reference length gradually increases starting from C
s
; the maximum deviation is reached at M
j
(C
s
<M
j
<C
e
); the deviation decreases gradually; and finally disappears at C
e
bp.
Normalization is performed by either expanding or compressing. Consider, for example in Model 1, normalization for the expression profile of P3 (12 h-1) in range (M1-M2 bp) against the reference P10 (96 h-2). Undoubtedly, the profile displays a systematic deviation from the reference. The degree of the deviation gradually increases starting from M2 bp to M1 bp probably because an intense peak generated near the shortest marker peak for the correction of M1 bp is used mistakenly. We expect the normalization will be achieved by a linear expansion of the short side (M1) of the range (M1-M2 bp) by anchoring the long side. The best approximating profile is found by considering various combinations of normalization candidates starting from D × 100% expansion to D × 100% compression of the short side at intervals of d bp. We set D = 0.4, as a maximal realistic displacement and d = 0.2. Accordingly, in practice, the number of combinations is 2 × (C e - C s ) × D/d + 1 (for example, there are 61 combinations of normalization candidates in the range (M1-M2 bp)) in Model 1.
For each combination x (x = {0, 1, ..., 2 × (C e - C s ) × D/d)}, we make a candidate profile P x by changing three parameters (L i , A i , and σ i ) accompanied by fragments (F i ) in the dissimilar range (C s - C e bp), according to the level of correction (expansion or compression). Those parameters are calculated as follows:



Candidates are made by substituting these transformed three-tuples

in a given range (C s - C e bp) into eq. (1). The best approximate profile is the one that achieves the highest correlation coefficient between Preferenceand P x (x = {0, 1, ..., 2 × (C e - C s ) × D / d}) in the range (C s - C e bp). In the normalization for the expression profile P3 in the range (M1-M2 bp) against the reference P10, the best normalized profile by our method matches well with the reference (Fig. 2).
A good example of Model 2 is the expression profile P2 (0 h-2) in range (M2-M4 bp) with the reference P10 (96 h-2); there is no possibility of Model 1 (C s ≠ M1) and the number of incorrect marker lengths is only one (M3). Model 2 is a mixture of Model 1. The normalization is also done by one of the {2 × (C e - C s ) × D / d + 1} combinations starting from D × 100% compression of the long side in (M2-M3 bp) and D × 100% expansion of the short side in (M3-M4 bp) to D × 100% expansion of the long side in (M2-M3 bp) and D × 100% compression of the short side in (M3-M4 bp) at intervals of d (= 0.2) bp. Unlike Model 1, we set D = 0.1 as a maximal realistic displacement. In the normalization for the expression profile P2 in the range (M2-M4 bp) against the reference, the best normalized profile by our method is matches well with the reference (Fig. 3).
It should be noted that when a dissimilar range (M j -Mj+lbp) is very wide (j = 1, 2,..., n M - l; l ≥ 3), there are two or more possibilities for incorrect marker lengths in Model 2. Of these cases, we only consider cases with j = 1 in Model 1 because such cases are the only realistic ones. For the remaining cases (j = 2,..., n M - l; l ≥ 3), the experiment should be redone rather than trying to normalize them by considering numerous possibilities. It should also be noted that there is a case of a dissimilar range (M1-M3 bp) to which both Models 1 and 2 are applicable. In this case, the best approximate profile is decided by comparing the two best possible profiles determined using Models 1 and 2.
References
Vos P, Hogers R, Bleeker M, Reijans M, van de Lee T, Hornes M, Frijters A, Pot J, Peleman J, Kuiper M, Zabeau M: AFLP: a new technique for DNA fingerprinting. Nucleic Acid Res 1995, 23: 4407–4414.
Vaneechoutte M: DNA fingerprinting techniques for microorganisms. Mol Biotechnol 1996, 6: 115–142.
Seppala H, He Q, Osterblad M, Huovinen P: Typing of group A streptococci by random amplified polymorphic DNA analysis. J Clin Microbiol 1994, 32: 1945–1948.
Desai M, Tanna A, Wall R, Efstratiou A, George R, Stanley J: Fluorescent amplified-fragment length polymorphism analysis of an outbreak of group A streptococcal invasive disease. J Clin Microbiol 1998, 36: 3133–3137.
Duim B, Wassenaar TM, Rigter A, Wagenaar J: High-resolution genotyping of Campylobacter strains isolated from poultry and humans with amplified fragment length polymorphism fingerprinting. Appl Environ Microbiol 1999, 65: 2369–2375.
Jonas D, Spitzmuller B, Weist K, Ruden H, Daschner FD: Comparison of PCR-based methods for typing Escherichia coli. Clin Microbiol Infect 2003, 9: 823–831. 10.1046/j.1469-0691.2003.00661.x
Augustynowicz E, Gzyl A, Szenborn L, Banys D, Gniadek G, Slusarczyk J: Comparison of usefulness of randomly amplified polymorphic DNA and amplified-fragment length polymorphism techniques in epidemiological studies on nasopharyngeal carriage of non-typable Haemophilus influenzae. J Med Microbiol 2003, 52: 1005–1014. 10.1099/jmm.0.05341-0
Diaz S, Pire C, Ferrer J, Bonete MJ: Identification of Phoenix dactylifera L. varieties based on amplified fragment length polymorphism (AFLP) markers. Cell Mol Biol Lett 2003, 8: 891–899.
Bachem CW, van der Hoeven RS, de Bruijn SM, Vreugdenhil D, Zabeau M, Visser RG: Visualization of differential gene expression using a novel method of RNA fingerprinting based on AFLP: analysis of gene expression during potato tuber development. Plant J 1996, 9: 745–753. 10.1046/j.1365-313X.1996.9050745.x
Savelkoul PH, Aarts HJ, de Haas J, Dijkshoorn L, Duim B, Otsen M, Rademaker JL, Schouls L, Lenstra JA: Amplified-fragment length polymorphism analysis: the state of an art. J Clin Microbiol 1999, 37: 3083–3091.
Fukumura R, Takahashi H, Saito T, Tsutsumi Y, Fujimori A, Sato S, Tatsumi K, Araki R, Abe M: A sensitive transcriptome analysis method that can detect unknown transcripts. Nucleic Acids Res 2003, 31: e94. 10.1093/nar/gng094
George KS, Zhao X, Gallahan D, Shirkey A, Zareh A, Esmaeli-Azad B: Capillary electrophoresis methodology for identification of cancer related gene expression patterns of fluorescent differential display polymerase chain reaction. J Chromatogr B Biomed Sci Appl 1997, 695: 93–102. 10.1016/S0378-4347(97)00115-1
Jones SW, Cai D, Weislow OS, Esmaeli-Azad B: Generation of multiple mRNA fingerprints using fluorescence-based differential display and an automated DNA sequencer. Biotechniques 1997, 22: 536–543.
Irie T, Oshida T, Hasegawa H, Matsuoka Y, Li T, Oya Y, Tanaka T, Tsujimoto G, Kambara H: Automated DNA fragment collection by capillary array gel electrophoresis in search of differentially expressed genes. Electrophoresis 2000, 21: 367–374. 10.1002/(SICI)1522-2683(20000101)21:2<367::AID-ELPS367>3.3.CO;2-T
Luehrsen KR, Marr LL, van der Knaap E, Cumberledge S: Analysis of differential display RT-PCR products using fluorescent primers and GENESCAN software. Biotechniques 1997, 22: 168–174.
Kyte J, Doolitle RF: A simple method for displaying the hydropathic character of a protein. J Mol Biol 1982, 157: 105–132. 10.1016/0022-2836(82)90515-0
Higasa K, Kukita Y, Baba S, Hayashi K: Software for machine-independent quantitative interpretation of SSCP in capillary array electrophoresis (QUISCA). Biotechniques 2002, 33: 1342–1348.
Drury HA, Green P, McCauley BK, Olson MV, Politte DG, Thomas LJ Jr: Spatial normalization of one-dimensional electrophoretic gel images. Genomics 1990, 8: 119–126. 10.1016/0888-7543(90)90233-K
Glasbey CA, Mardia KV: A penalised likelihood approach to image warping. J Royal Statist Soc B 2001, 63: 465–514. 10.1111/1467-9868.00295
Lemkin PF: Comparing two-dimensional electrophoretic gel images across the Internet. Electrophoresis 1997, 18: 461–470.
Salmi J, Aittokallio T, Westerholm J, Griese M, Rosengren A, Nyman TA, Lahesmaa R, Nevalainen O: Hierarchical grid transformation for image warping in the analysis of two-dimensional electrophoresis gels. Proteomics 2002, 2: 1504–1515. 10.1002/1615-9861(200211)2:11<1504::AID-PROT1504>3.0.CO;2-B
Skovgaard IM, Jensen K, Sondergaard I: From image processing to classification: III. Matching patterns by shifting and stretching. Electrophoresis 1995, 16: 1385–1389.
Takahashi H, Umeda N, Tsutsumi Y, Fukumura R, Ohkaze H, Sujino M, van der Horst G, Yasui A, Inoue ST, Fujimori A, Ohhata T, Araki R, Abe M: Mouse dexamethasone-induced RAS protein 1 gene is expressed in a circadian rhythmic manner in the suprachiasmatic nucleus. Brain Res Mol Brain Res 2003, 110: 1–6. 10.1016/S0169-328X(02)00543-0
Araki R, Takahashi H, Fukumura R, Sun F, Umeda N, Sujino M, Inoue SI, Saito T, Abe M: Restricted expression and photic induction of a novel mouse regulatory factor X 4 transcript in the suprachiasmatic nucleus. J Biol Chem 2004, 279: 10237–10242. 10.1074/jbc.M312761200
Aittokallio T, Ojala P, Nevalainen TJ, Nevalainen O: Analysis of similarity of electrophoretic patterns in mRNA differential display. Electrophoresis 2000, 21: 2947–2956. 10.1002/1522-2683(20000801)21:14<2947::AID-ELPS2947>3.0.CO;2-N
Aittokallio T, Ojala P, Nevalainen TJ, Nevalainen O: Automated detection of differently expressed fragments in mRNA differential display. Electrophoresis 2001, 22: 1935–1945. 10.1002/1522-2683(200106)22:10<1935::AID-ELPS1935>3.0.CO;2-5
Aittokallio T, Pahikkala T, Ojala P, Nevalainen TJ, Nevalainen O: Electrophoretic signal comparison applied to mRNA differential display analysis. Biotechniques 2003, 34: 116–122.
Acknowledgements
This work was supported by a Research Revolution 2002 on Innovative Development Project grant.
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
KK invented the method and wrote the paper. RF made critical comments in light of the HiCEP experimental technique. JJR edited the paper. RA and MA provided critical comments and led the project.
Electronic supplementary material
12859_2004_368_MOESM2_ESM.png
Additional File 2: Magnified electrophoretic patterns and the quality profiles in range (35–50 bp) in Fig. 4. Descriptions are the same as those in Fig. 4. Visual evaluation confirmed the validity of the normalizations (2.7% compression of the short side of the range) for two lanes (0 h-2 and 12 h-2) which are suspected false-positive errors. (PNG 16 KB)
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
About this article
Cite this article
Kadota, K., Fukumura, R., Rodrigue, J.J. et al. A normalization strategy applied to HiCEP (an AFLP-based expression profiling) analysis: Toward the strict alignment of valid fragments across electrophoretic patterns. BMC Bioinformatics 6, 43 (2005). https://doi.org/10.1186/1471-2105-6-43
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2105-6-43







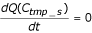 and C
tmp_s
<C
seed_s
; similarly, C
tmp_e
,
and C
tmp_s
<C
seed_s
; similarly, C
tmp_e
,  and C
tmp_e
<C
seed_e
and C
tmp_e
<C
seed_e